Pensamos aquí en una región del plano encerrada por una curva. El área de esa región puede calcularse mediante integral definida; la expresión de esa integral depende de cómo venga dada la curva.

 

Curva en explícitas cartesianas

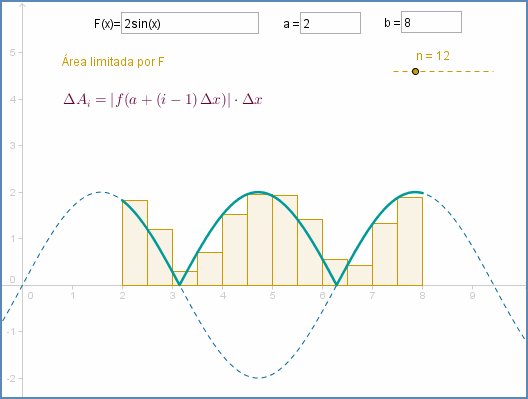
• El área limitada entre $y=f(x)$, el eje $OX$ y las rectas $x=a$ y $x=b$ es
\begin{equation}\label{t1e1}\mbox{Área}=\int_a^b |f(x)|\, dx\end{equation}
• El área limitada entre dos gráficas, sean $y=f(x)$ e $y=g(x)$, y las rectas $x=a$ y $x=b$ es $$\mbox{Área}=\int_a^b |f(x)-g(x)|\, dx$$

Laboratorio: Aplicaciones de la integral

 

 

Curva en paramétricas

 

Si la curva $C$ viene dada por las ecuaciones paramétricas $x=x(t)$ e $y=y(t)$ con $t\in[t_1,t_2]$

• El área limitada entre $C$ y el eje $OX$ es $$\mbox{Área}=\int_{t_1}^{t_2} |y(t)x'(t)|\, dt$$
• El área limitada entre $C$ y el eje $OY$ es $$\mbox{Área}=\int_{t_1}^{t_2} |x(t)y'(t)|\, dt$$

Estas fórmulas se obtienen de hacer un cambio de variable apropiado en (1) .

 

Curva en polares

 

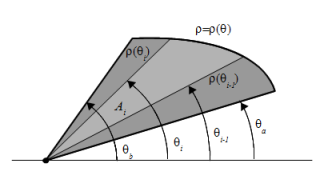
El área encerrada por la curva $r=r(\theta)$ para $\theta\in[\theta_a,\theta_b]$ es

\begin{equation}\label{t1e2}\mbox{Área}=\frac{1}{2}\int_{\theta_a}^{\theta_b} r(\theta)^2\, d\theta\end{equation}

 

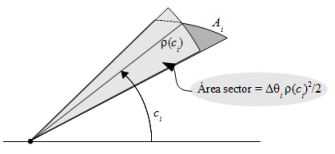
Esta fórmula se obtiene de considerar una partición del intervalo $[\theta_a,\theta_b]$, y en cada subregión tomar como área aproximada el área de un sector circular: si el subintervalo es $[\theta_{i-1},\theta_i]$ el sector aproximante tendrá ángulo igual a $\Delta \theta_i=\theta_i- \theta_{i-1}$ y como radio se tomará un $r=r(c_i)$ siendo $c_i$ cualquiera del subintervalo $[\theta_{i-1},\theta_i]$; por tanto su área es $r(c_i)\Delta \theta_i/2$; sumando todas estas áreas y haciendo tender la norma de la partición a cero obtendremos la expresión anterior.

 

Ejercicios interactivos:

Curvas en cartesianas

• Área encerrada por dos curvas. Ejemplo 1
• Área encerrada por dos curvas. Ejemplo 2



Curvas en paramétricas

• Laboratorio curvas en paramétricas
• Área encerrada por una elipse
• Área encerrada por la cicloide



Curvas en polares

• Laboratorio curvas en polares
• Área común a dos círculos
• Área encerradas en la cardioide
• Propiedades de una espiral