Teniendo en cuenta cómo se calcula el valor medio de la temperatura en un alambre, debemos calcular la longitud de la curva y la integral de la temperatura sobre ella.

Paso 1

Partiendo de la expresión polar de la curva, encuentra el elemento diferencial de arco en polares. Pulsa en 'Ver' cuando lo tengas.

Paso 2

Ahora calculamos la longitud. El resultado es

Paso 3

Calcular la integral de la temperatura a lo largo de la curva. Puesto que en la curva $C$ las coordenadas $x$ e $y$ son $$x=e^t\cos t\hspace{.2cm},\hspace{.3cm} y=e^t\,\mbox{sen}\, t$$ la temperatura en los puntos de la curva es $$T(x(t),y(t))=\cos(e^t\cos t)\, \mbox{sen}(e^t\cos t-e^t\,\mbox{sen}\, t)$$ La integral que buscamos es $$I=\sqrt{2}\int_0^\pi T(x(t),y(t)) e^t\, dt$$ Llegados a este punto reconocemos que necesitamos la ayuda del ordenador. Podemos pedirle que nos calcule esta integral o también, si queremos escribir expresiones más sencillas, podemos darle la forma de la función temperatura y de las componentes de la curva y que calcule la temperatura media. Inténtalo y pulsa en 'Ver'.

syms t
x=exp(t)*cos(t);
y=exp(t)*sin(t);
temp=cos(x)*sin(x-y);
integral=sqrt(2)*double(int(temp*exp(t),t,0,pi));
longitud=sqrt(2)*(exp(pi)-1);
tempmedia=integral/longitud

tempmedia =
   -0.0862

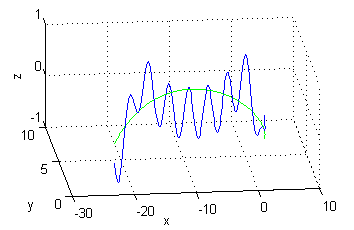
Resolución del segundo apartado

Para calcular la integral $$I=\int_C \nabla T(x,y)\cdot d{\bf r}$$ podemos utilizar el teorema fundamental, puesto que se trata de una integral de línea de un campo gradiente. Comprueba que se cumplen las condiciones, calcula la integral y pulsa en 'Ver'.

Otra opción para encontrar esta integral es recurrir al hecho de que la integral de un campo gradiente a lo largo de una curva cerrada es nulo, siempre que el campo potencial sea de clase $C^1$ en una región que contenga a la curva. Este hecho puede obtenerse tanto del teorema de Green como del teorema fundamental. Realmente en el caso que nos ocupa sería más recomendable obtener la integral como se ha hecho antes, pues la función potencial es conocida. Si no lo fuera, puede ser interesante proceder como sigue: puesto que la curva no es cerrada, tomaremos una curva que la incluya y que sí sea cerrada. Podemos unir $C$ con el segmento $L$ del eje $OX$ entre los puntos $(-e^\pi,0)$ y $(1,0)$

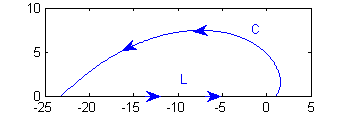
Puesto que $$I=\oint_{C\cup L} \nabla T(x,y)\cdot d{\bf r}=0$$ y debido a la aditividad de la integral, $$I=\oint_{C\cup L} \nabla T(x,y)\cdot d{\bf r}= \int_C \nabla T(x,y)\cdot d{\bf r}+\int_L \nabla T(x,y)\cdot d{\bf r}$$ nos bastará calcular la integral a lo largo del segmento $L$: $$\int_C \nabla T(x,y)\cdot d{\bf r}=-\int_L \nabla T(x,y)\cdot d{\bf r}$$ Halla esa integral y pulsa en 'Ver'

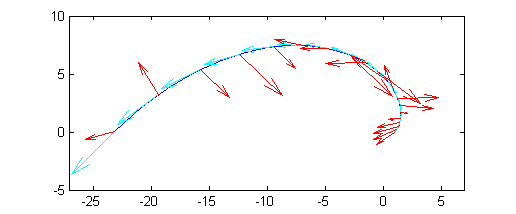
Resolución del tercer apartado

Si por alguna razón no se pudieran aplicar estos teorema y tuviera que realizarse la integral de línea directamente, es decir, evaluando el gradiente sobre la curva, multiplicándolo por el diferencial de curva e integrando en la variación del parámetro, sería aconsejable utilizar el ordenador. Podemos seguir los siguientes pasos: (tras realizar cada uno, pulsa en 'Continuar')

• declara simbólicas las variables t, x e y

Continuar

syms t x y

• define la función $T(x,y)$

Continuar

temp=cos(x)*sin(x-y); % campo escalar de temperaturas

• define las componentes de la curva

Continuar

xc=exp(t)*cos(t); % primera componente de la curva
yc=exp(t)*sin(t); % segunda componente de la curva

• calcula el diferencial, $d{\bf r}=(dx,dy)$, de la curva

Continuar

dx=diff(xc,t);dy=diff(yc,t); % derivadas de las componentes de la curva

• calcula las componentes del grandiente de $T$

Continuar

M=subs(diff(temp,x),{x,y},{xc,yc}); % primera componente del campo flujo de calor
N=subs(diff(temp,y),{x,y},{xc,yc}); % segunda componente del campo flujo de calor

• halla el valor de la integral del producto escalar $(M,N)\cdot d{\bf r}$ entre 0 y $\pi$.

Continuar

integral=double(int(sum([M, N].*[dx, dy]),t,0,pi))

Ejecutando

syms x y t
temp=cos(x)*sin(x-y); % campo escalar de temperaturas
xc=exp(t)*cos(t); % primera componente de la curva
yc=exp(t)*sin(t); % segunda componente de la curva
dx=diff(xc,t);dy=diff(yc,t); % derivadas de las componentes de la curva
M=subs(diff(temp,x),{x,y},{xc,yc}); % primera componente del campo flujo de calor
N=subs(diff(temp,y),{x,y},{xc,yc}); % segunda componente del campo flujo de calor
integral=double(int(sum([M, N].*[dx, dy]),t,0,pi))

obtendremos $-0.8278$ como valor de esta integral. Continuar

Resolución del cuarto apartado

Se trata ahora de realizar la integral $$F=\int_C {\nabla T}(x,y)\cdot d{\bf n}$$ siendo ${\bf n}$ la normal unitaria que tiene componente segunda positiva en la mayor parte de los puntos. En la figura siguiente puedes ver una muestra del campo vectorial ${\nabla T}$ (en rojo) y una muestra de vectores normales (en verde) a la curva.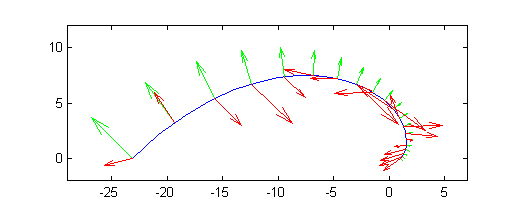

El vector normal en cada punto $(x(t),y(t))$, todavía sin normalizar a uno, es

Así pues, la integral que hemos de hallar es $$F=\int_0^\pi (M(x(t),y(t)),N(x(t),y(t)))\cdot (y'(t),-x'(t))\, dt$$ siendo $M$ y $N$ las componentes del campo $\nabla T$. Para hacerla en el ordenador, basta añadir la siguiente línea a las que se habían escrito en el apartado anterior:

flujosal=double(int(sum([M, N].*[dy, -dx]),t,0,pi))

El valor de este flujo resulta $-5.1331$.