Enunciado
Se considera la ecuación diferencial de primer orden $$y'=x-y$$
- Comprueba que verifica las condiciones suficientes de existencia y unicidad de solución por cada punto $(x_0,y_0)$ del plano.
- Encuentra la solución que pasa por el punto $(x_0,y_0)$.
- Escribe la expresión de la isoclina de pendiente $\alpha$. Dibuja en una figura al menos cinco isoclinas y sobre ellas una muestra del campo de direcciones.
- Analiza el comportamiento de las soluciones en cuanto a monotonía y concavidad, así como la existencia de extremos (máximos o mínimos) y de puntos de inflexión.
Resolución del primer apartado
Tenemos que aplicar el teorema de
existencia y unicidad de solución de un p.v.i de primer orden.
Escribimos la ecuación como $$y'=f(x,y)=x-y$$ Las hipótesis se cumplen puesto que:
- la función $f(x,y)=x-y$ es continua en todo el plano
- su derivada parcial respecto de $y$ es $f'_y(x,y)=-1$, que obviamente es continua en todo el plano
Resolución del segundo apartado
Paso 1
Encontrar la solución general: Hemos de reconocer en primer lugar que la ecuación se ajusta a la forma $$y'+p(x)y=q(x)$$ que la caracteriza como lineal. Podemos resolverla por tanto mediante la aplicación del factor integrante $$\mu(x)=e^{\int p(x)\, dx}$$ Busca el factor integrante y pulsa en 'Continuar' cuando lo tengas.
En este caso el factor integrante es $\mu(x)=e^x$ y por tanto la solución cumple que $$e^xy=\int xe^x\, dx$$ Encontramos esa primitiva integrando por partes, para llegar a que
$e^xy=xe^x-e^x$ luego $y=x-1$
$e^xy=xe^x-e^x$ pero hay que añadir la constante, luego $y=x-1+C$
Ninguna de las dos opciones presentadas es correcta.
No es correcto. ¿No debería obtenerse una familia uniparamétrica?
Pero la constante se suma en la primitiva, antes de multiplicar por $e^{-x}$
En efecto, ninguna de las dos son correctas. Al hacer la primitiva hemos de tener en cuenta la constante de integración, de manera que
$$e^xy=xe^x-e^x+C$$
de donde $$y=x-1+Ce^{-x}$$
es la solución general de la ecuación.
Paso 2
Hallar la solución particular: debemos imponer que la solución pase por el punto $(x_0,y_0)$, despejar la constante, que en este caso quedará en función de $x_0$ y de $y_0$ y después introducir de nuevo la constante en la función. Inténtalo y pulsa en 'Ver' cuando lo tengas.
Ver
- Para que la función pase por $(x_0,y_0)$ debe cumplirse que $y_0=x_0-1+Ce^{-x_0}$
- despejando la constante: $C=(y_0-x_0+1)e^{x_0}$
- e introduciéndola en la función obtenemos la solución particular buscada $$y=x-1+(y_0-x_0+1)e^{x_0-x}$$
Resolución del tercer apartado
Hemos de saber qué son las isoclinas de una ecuación de primer orden. Ahora es fácil encontrar la expresión de la isoclina correspondiente a la pendiente $\alpha$ de la ecuación $y'=x-y$... Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
La isoclina correspondiente a la pendiente $\alpha$ es la recta $y=x-\alpha$. Puesto que debemos dibujar cinco de ellas elegiremos las cinco más sencillas de dibujar, que son las correspondientes a $\alpha=-2$, $\alpha=-1$, $\alpha=0$, $\alpha=1$ y $\alpha=2$, es decir las rectas
$$y=x+2 \ \ ,\ \ y=x+1 \ \ ,\ \ y=x \ \ ,\ \ y=x-1 \ \ ,\ \ y=x-2$$
Podemos dibujarlas por ejemplo en el cuadrado $[-2,2]\times[-2,2]$:
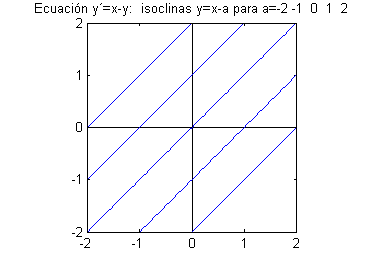
Para dibujar una muestra del
campo de direcciones debemos trazar, para cada isoclina, un pequeño segmento de recta tangente sobre algunos de sus puntos. Obviamente, los segmentos sobre la isoclina correspondiente a $\alpha=-2$, deben tener pendiente $-2$, los que pintemos sobre la correspondiente a $\alpha=-1$ serán de pendiente $-1$ y así para todas las demás:
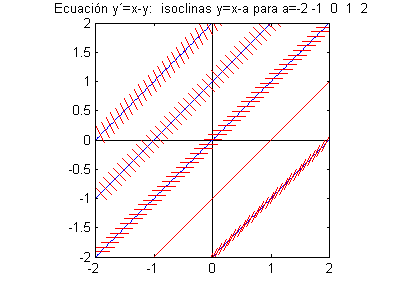
Resolución del cuarto apartado
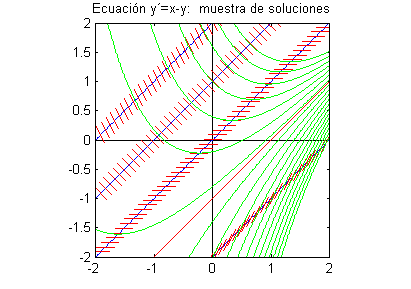
Para hacer este análisis, lo más fácil es utilizar la propia ecuación. Las soluciones son crecientes donde su derivada sea positiva, luego para las soluciones de $y'=x-y$ esto ocurrirá en $y<x$. La recta $y=x$ divide el plano en dos regiones: sobre $y=x$ las curvas solución son crecientes y bajo $y=x$ son decrecientes. Queda por saber si las curvas solución cortan a $y=x$, lo que en este caso equivale a la existencia de puntos donde cambiarían de decrecientes a crecientes, es decir, mínimos. ¿Las curvas solución pasan por los puntos de $y=x$?
Vimos antes que por cualquier punto del plano pasa una solución, luego sí existen mínimos.
El razonamiento presentado no es correcto para cualquier caso.
Ese razomiento comienza bien, pues en efecto por cada punto de $y=x$ pasa una solución, pero para saber si es una solución que ha sido decreciente, debemos asegurarnos que $y=x$ no es ella misma una solución.
En efecto, el razonamiento de la otra propuesta comienza bien, pues en efecto por cada punto de $y=x$ pasa una solución; pero para saber si es una solución que ha sido decreciente antes de cortar a $y=x$ para pasar a ser creciente, debemos asegurarnos que $y=x$ no es ella misma una solución. Compruébalo y pulsa en 'Continuar'.
Puesto que en efecto $y=x$ no es solución de la ecuación:
$$y=x \hspace{1.5cm} \Longrightarrow \hspace{1.5cm} \left\{\begin{array}{l}y'=1\\ x-y=0\end{array}\right.$$
está garantizada la existencia de mínimos, pues algunas curvas solución pasan de la región $y>x$ (donde son decrecientes) a la región $y<x$ (donde son crecientes).
Debemos ahora hacer el análisis de la concavidad. Para ello debes escribir $y''$ en función de $x$ e $y$, derivando la ecuación diferencial:
$$y'=x-y \hspace{1cm}\Rightarrow \hspace{1cm} y''=1-y'=1-x+y$$
Por tanto, las soluciones son
Cóncavas en $y>x-1$ con sus puntos de inflexión en $y=x-1$
Convexas en $y>x-1$ con sus puntos de inflexión en $y=x-1$
Cóncavas en $y>x-1$ y convexas en $y<x-1$, pero no tienen puntos de inflexión
Es cierto que las soluciones son cóncavas en $y>x-1$, pero no es correcta la afirmación respecto de los puntos de inflexión.
Las dos afirmaciones de esta opción son incorrectas.
Puesto que en la región $y>x-1$ la segunda derivada de las soluciones es positiva, sabemos que son cóncavas cuando transcurren por esa región. Obviamente en la región $y<x-1$ serán convexas. la cuestión aquí es si hay soluciones que cortan a $y=x-1$ y que por tanto pasarían de cóncavas a convexas o no. Por los puntos de $y=x-1$ deben pasar soluciones, pero si la función $y=x-1$ es solución de la ecuación no podrán existir, en virtud del teorema de unicidad, otras soluciones pasando por sus puntos. Comprobamos que $y=x-1$ es solución:
$$y=x-1 \hspace{1.5cm} \Longrightarrow \hspace{1.5cm} \left\{\begin{array}{l}y'=1\\ x-y=1\end{array}\right.$$
Por tanto, por los puntos de $y=x-1$ sólo pasa la solución $y=x-1$; las otras soluciones no la cortan, de manera que el plano queda dividido en dos regiones (por encima y por debajo de $y=x-1$) que no 'comparten' soluciones y éstas son o bien siempre cóncavas o bien siempre convexas.