Enunciado
Encuentra la transformada inversa de $$F(s)=\frac{3se^{-4s/3}}{s^2+4s+10}$$ Comprueba el resultado con el ordenador y representa las funciones $F(s)$ y ${\cal L}^{-1}[F]$.
Resolución del primer apartado
Paso 1
La presencia del factor $e^{-4s/3}$ apunta al uso de la propiedad de la transformada de Laplace relativa a ...
Ninguna de las opciones presentadas es correcta.
No es correcto.
No es correcto.
No es correcto.
En efecto, ninguna de las opciones presentadas es adecuada en este caso, ya que la presencia del factor $e^{-4s/3}$ apunta al uso de la propiedad de traslación en la variable $t$. Si $f(t)={\cal L}^{-1}[F(s)]$, entonces
$$f(t)=3{\cal L}^{-1}[\frac{se^{-4s/3}}{s^2+4s+10}]=3g(t-\frac{4}{3})U(t-\frac{4}{3})$$
siendo $$g(t)={\cal L}^{-1}\frac{s}{s^2+4s+10}$$
Paso 2
Hallar $g(t)$. Para ello debemos empezar completando cuadrados en el polinomio del denominador. Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
$$s^2+4s+10=(s+2)^2+6$$
luego debemos escribir
$$\frac{s}{s^2+4s+10}=\frac{s+2}{(s+2)^2+6}-\frac{2}{(s+2)^2+6}$$
y así reconocer a $\frac{s}{s^2+4s+10}$ como la resta de dos funciones trasladadas de $s$ a $s+2$. Esas dos funciones son
$$H_1(s)=\frac{s}{s^2+6} \hspace{.6cm} \mbox{y} \hspace{.6cm} H_2(s)=\frac{2}{s^2+6}$$
Sus transformadas inversas las podemos obtener casi de forma inmediata de la
tabla básica de transformadas; escribe $h_1(t)={\cal L}^{-1}[H_1]$ y $h_2(t)={\cal L}^{-1}[H_2]$ y pulsa en 'Continuar'.
$$h_1(t)={\cal L}^{-1}[\frac{s}{s^2+6}]=\cos \sqrt{6}t \hspace{.6cm} \mbox{y} \hspace{.6cm} h_2(t)={\cal L}^{-1}[\frac{2}{s^2+6}]=\frac{2}{\sqrt{6}}\mbox{sen}\, \sqrt{6}t=\frac{\sqrt{6}}{3}\mbox{sen}\, \sqrt{6}t$$
Ahora, puesto que $$\frac{s}{s^2+4s+10}=\frac{s+2}{(s+2)^2+6}-\frac{2}{(s+2)^2+6}$$
utilizaremos la propiedad de la traslación en la variable $s$. Hazlo tú y pulsa en 'Ver'.
Ver
$$g(t)={\cal L}^{-1}[\frac{s}{s^2+4s+10}]=e^{-2t}(\cos \sqrt{6}t-\frac{\sqrt{6}}{3}\mbox{sen}\, \sqrt{6}t)$$
con lo cual
$$f(t)=3g(t-\frac{4}{3})U(t-\frac{4}{3})=e^{-2(t-4/3)}\left[3\cos \sqrt{6}(t-\frac{4}{3})-\sqrt{6}\mbox{sen}\, \sqrt{6}(t-\frac{4}{3})\right]U(t-\frac{4}{3})$$
Paso 3
Comprobación del resultado con el ordenador y representación de las funciones. Escribe en un fichero las líneas de código con las que- declaras 's' como variable simbólica
- defines 'F' para que guarde la expresión de $F(s)$
- activas la figura 1 ('figure(1)')
- dibujas con 'ezplot' la función 'F' entre $-2$ y 4
- activas la figura 2
- defines 'f' como la transformada inversa de 'F' (con 'ilaplace')
- dibujas con 'ezplot' la función 'F' entre 1 y 2
Ver
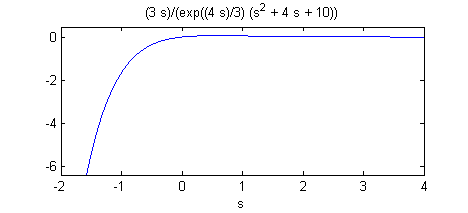
syms s F=3*s*exp(-4*s/3)/(s^2+4*s+10); figure(1) ezplot(F,[-2,4]) figure(2) f=ilaplace(F) ezplot(f,[1,2])Cuando ejecutemos este fichero, obtendremos en la ventana de comandos la transformada inversa:
f = 3*heaviside(t - 4/3)*exp(8/3 - 2*t)*(cos(6^(1/2)*(t - 4/3)) - (6^(1/2)*sin(6^(1/2)*(t - 4/3)))/3)en la ventana 'Figure 1':
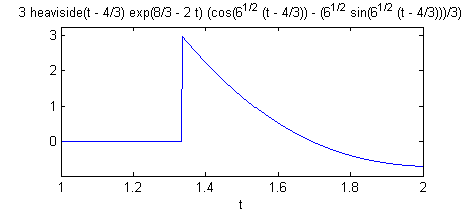
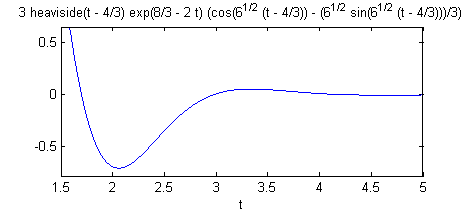
Puede ser interesante ver la gráfica de la función $f(t)$ para valores más alejados. Por ejemplo con
ezplot(f,[1.5,5])obtendremos