Enunciado
Situamos una placa delgada en el plano XY, ocupando la región $4x^2+y^2\leq 4$. La temperatura, $T$ medida en grados centígrados, es en todos los puntos mayor o igual a $1^o$C; en cada punto está relacionada con las coordenadas $(x,y)$ del punto, medidas en cm., por la ecuación $$4x^2+y^2+4(T-1)^2=4$$
- Determina las razones de cambio de la temperatura respecto de $x$ y respecto de $y$ en cada punto $(x,y)$ de la placa. ¿Cómo cambia la temperatura si desde el punto $(\frac{1}{2},-\sqrt{2})$ nos movemos medio cm. a la izquierda? ¿Y si nos movemos la misma distancia hacia arriba?
- ¿Cuál es la velocidad de variación de la temperatura si vamos desde $(\frac{1}{2},-\sqrt{2})$ hacia el punto $(0,0)$?
- ¿Existe alguna dirección desde $(\frac{1}{2},-\sqrt{2})$ en la que la temperatura aumente $1^o$C si nos desplazamos medio centímetro?
- ¿Existe alguna dirección desde $(\frac{1}{2},-\sqrt{2})$ en la que la temperatura aumente medio $^o$C si nos desplazamos medio cm.?
Resolución del primer apartado
Paso 1
Por la definición de derivada parcial , sabemos que la derivada parcial respecto de $x$ es la razón de cambio de la temperatura respecto de $x$. Lo mismo ocurre con la variable $y$. Así pues, lo primero que hemos de hacer es encontrar esas derivadas parciales. Puesto que estamos ante una ecuación implícita $$4x^2+y^2+4(T-1)^2=4$$ derivaremos implícitamente. El resultado es:
Respecto de $x$ será $8x+2yy'_x+8(T-1)T'_x=0$ y respecto de $y$ será $8xx'_y+2y+8(T-1)T'_y=0$
Respecto de $x$ será $8x+8(T-1)T'_x=0$ y respecto de $y$ será $2y+8(T-1)T'_y=0$
No es correcto; las variables $x$ y $y$ son libres entre sí, no están ligadas. La variable $x$ no depende de $y$ y la variable $y$ no depende de la $x$.
Estas sí son correctas. Lo que significa que la razón de cambio de $T(x,y)$ respecto de $x$ es $$\frac{-x}{T(x,y)-1}$$ y la razón de cambio de $T(x,y)$ respecto de $y$ es $$\frac{-y}{4(T(x,y)-1)}$$
luego en cualquier $(x,y)$, el gradiente de la temperatura es
$$\nabla T(x,y)=\left(\frac{-x}{T(x,y)-1},\frac{-y}{4(T(x,y)-1)}\right)$$
Ahora debemos determinar cuánto cambia $T(x,y)$ si nos movemos de $(\frac{1}{2},-\sqrt{2})$.
Paso 2
Hallamos $\nabla T(\frac{1}{2},-\sqrt{2})$. Este vector es
$$\nabla T(\frac{1}{2},-\sqrt{2})=\left(\frac{-1}{2(T(x,y)-1)},\frac{\sqrt{2}}{4(T(x,y)-1)}\right)$$
$$\nabla T(\frac{1}{2},-\sqrt{2})=\left(\frac{-1}{2(0-1)},\frac{\sqrt{2}}{4(0-1)}\right)=\left(\frac{1}{2},\frac{-\sqrt{2}}{4}\right)$$
Ninguna de las dos opciones presentadas es correcta.
$\nabla T(\frac{1}{2},-\sqrt{2})$ es un vector de números; no puede depender de $x$ e $y$;
¿Por qué $T(x,y)=0$?
En efecto, ninguna es correcta. Para hallar este gradiente necesitamos conocer el valor de $T(\frac{1}{2},-\sqrt{2})$. Inténtalo y pulsa en 'Continuar' cuando lo tengas.
Sustituyendo $x=\frac{1}{2}$ e $y=-\sqrt{2}$ en la expresión $4x^2+y^2+4(T-1)^2=4$,
$$4\frac{1}{4}+2+4(T-1)^2=4\ \ \Rightarrow \ \ T=1\pm \frac{1}{2}$$
Puesto que $T>1$, $$T(\frac{1}{2},-\sqrt{2})=\frac{3}{2}$$
Ahora ya puedes calcular el gradiente en ese punto; pulsa en 'Ver' cuando lo tengas.
Ver
$$\nabla T(\frac{1}{2},-\sqrt{2})=(-1,\frac{\sqrt{2}}{2})$$
A continuación puedes ver un dibujo de la placa coloreada según la temperatura (el color más cálido indica mayor temperatura) y el vector gradiente de la temperatura en el punto $(\frac{1}{2},-\sqrt{2})$:
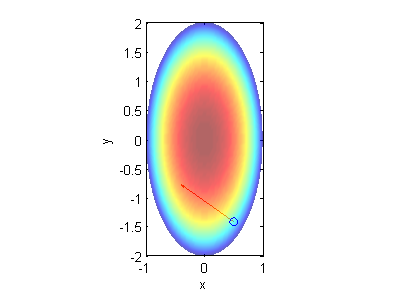

Paso 3
Utilizamos ese gradiente para saber- ¿Cuánto varía aproximadamente $T(x,y)$ cuando nos movemos $\frac{1}{4}$ cm. a la izquierda de $(\frac{1}{2},-\sqrt{2})$? Puesto que en ese movimiento la coordenada $y$ permanece constante, utilizaremos la razón de cambio respecto de $x$, $$T'_x(\frac{1}{2},-\sqrt{2})=-1 \hspace{.3cm} (^o\mbox{C}/\mbox{cm})$$ Para producir un desplazamiento hacia la izquierda y de $1/4$ cm, el incremento de $x$ es $$\Delta x=\frac{-1}{4}\hspace{.3cm} (\mbox{cm})$$ por tanto la variación de temperatura, $\Delta T$, se aproxima así $$\Delta T\approx T'_x(\frac{1}{2},-\sqrt{2})\Delta x=\frac{1}{4} \hspace{.3cm} (^o\mbox{C})$$ Luego la temperatura pasará de $\frac{3}{2}=1.5 ^o$C a $1.75 ^o$C. Puedes pensar que esto lo calcularías más rápido y con más precisión utilizando la fórmula $4x^2+y^2+4(T-1)^2=4$ con los valores adecuados de $x$ e $y$; es cierto en este caso; pero procedemos así para mostrar cómo se estima la variación de temperatura disponiendo únicamente del gradiente y del valor de la función en un sólo punto, sin conocer la expresión de la función en los demás puntos.
- ¿Cuánto varía aproximadamente $T(x,y)$ cuando nos movemos $\frac{1}{4}$ cm. hacia arriba desde $(\frac{1}{2},-\sqrt{2})$? Hazlo tú y pulsa en 'Ver'.
Ver
Puesto que en ese movimiento la $x$ permanece constante, haremos
$$\Delta T\approx T'_y(\frac{1}{2},-\sqrt{2})\Delta y=\frac{\sqrt{2}}{2}\frac{1}{4}=\frac{\sqrt{2}}{8} \hspace{.3cm} (^o\mbox{C})$$
y ésta será la variación aproximada de la temperatura en ese supuesto.
Resolución del segundo apartado
Paso 1
Cálculo de la dirección correspondiente a ese movimiento: si vamos hacia el punto $(0,0)$ desde el punto $(\frac{1}{2},-\sqrt{2})$, la dirección es
$${\bf u}=(\frac{1}{2},-\sqrt{2})$$
$${\bf u}=(-\frac{1}{2},\sqrt{2})$$
$${\bf u}=\frac{2}{3}(\frac{1}{2},-\sqrt{2})$$
Ninguna de las anteriores
Ese vector no es una dirección, pues su módulo no es 1.
Ese vector no es una dirección, pues su módulo no es 1.
Es una dirección, pues su módulo es 1, pero tiene sentido opuesto al que se precisa aquí.
En efecto, ninguna de las propuestas es correcta. Hacemos el vector restando las coordenadas del punto de salida del de llegada y después dividimos este vector por su norma:
$${\bf v}=\overline{(\frac{1}{2},-\sqrt{2})(0,0)}=(-\frac{1}{2},\sqrt{2}) \ \ \Rightarrow \ \ {\bf u}=\frac{2}{3}(-\frac{1}{2},\sqrt{2})$$
En la figura vemos este vector sobre la placa.
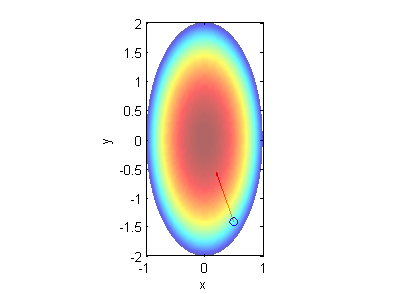

Paso 2
Una vez que sabemos la dirección del movimiento podemos calcular la velocidad de variación de la temperatura, pues ése valor es la derivada direccional. Hazlo tú y pulsa en 'Ver'.
Ver
Puesto que disponemos del gradiente, la derivada direccional es fácil de calcular:
$$D_{\bf u} T(\frac{1}{2},-\sqrt{2})= \nabla T (\frac{1}{2},-\sqrt{2})\cdot {\bf u} =1 \hspace{.3cm} (^o\mbox{C}/\mbox{cm})$$
Resolución del tercer apartado
Hemos de averiguar si existe alguna dirección desde $(\frac{1}{2},-\sqrt{2})$ en la que la temperatura aumente $1^o$C si nos desplazamos medio centímetro. Esto es equivalente a que exista alguna dirección desde ese punto según la cual la derivada direccional, $D_{\bf u} T(\frac{1}{2},-\sqrt{2})$, cumpla $$\Delta T= D_{\bf u} T(\frac{1}{2},-\sqrt{2}) \Delta x =D_{\bf u} T(\frac{1}{2},-\sqrt{2}) \frac{1}{2}=1$$ es decir, valga 2. Por las propiedades del gradiente sabemos que las derivadas direccionales de $T$ en $(\frac{1}{2},-\sqrt{2})$ no pueden sobrepasar $|T(\frac{1}{2},-\sqrt{2})|$. Así que la respuesta a la pregunta del apartado es $\ldots$ hazlo tú y pulsa en 'Ver'.
Ver
$$|T(\frac{1}{2},-\sqrt{2})|=|(-1,\frac{\sqrt{2}}{2})|=\sqrt{\frac{3}{2}}< 2$$
Luego no existe tal dirección.
Resolución del cuarto apartado
Debemos analizar ahora si existe alguna dirección desde $(\frac{1}{2},-\sqrt{2})$ en la que la temperatura aumente medio $^o$C si nos desplazamos medio cm. ¿Cuánto debería valer la derivada direccional? Calcúlala, analiza si es posible que exista y pulsa en 'Ver'.
Ver
$$\Delta T=1 \hspace{.3cm} \Rightarrow \hspace{.3cm} D_{\bf u} T(\frac{1}{2},-\sqrt{2}) \frac{1}{2}=\frac{1}{2} \hspace{.3cm} \Rightarrow \hspace{.3cm} D_{\bf u} T(\frac{1}{2},-\sqrt{2})=1$$
Puesto que esta derivada es menor que el módulo del gradiente en ese punto, podemos buscar la dirección ${\bf u}=(a,b)$ tal que
$${\bf u}\cdot \nabla T(\frac{1}{2},-\sqrt{2})=1$$
De esta igualdad resulta la ecuación $$-a+\frac{\sqrt{2}}{2}b=1$$
y por ser ${\bf u}=(a,b)$ una dirección, $$a^2+b^2=1$$
Con lo cual
$$a=\frac{\sqrt{2}}{2}b-1 \hspace{.3cm} \Rightarrow \hspace{.3cm} \frac{3}{2}b^2-\sqrt{2}b=0$$
de donde obtenemos dos posibles direcciones
$${\bf u_1}=(-1,0) \hspace{.3cm} \mbox{y} \hspace{.3cm} {\bf u_2}=(-\frac{1}{3},\frac{2\sqrt{2}}{3})$$
En la figura vemos estas dos direcciones sobre la placa:
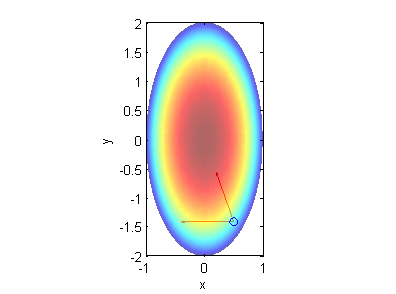

Resumen
- Primer apartado
- calcular el gradiente en todos los puntos
- hallarlo en el punto dado
- utilizarlo para estimar variaciones de la temperatura
- Segundo apartado
- hallar la dirección que corresponde al movimiento descrito
- calcular la derivada direccional respecto a esa dirección
- Tercer apartado
- hallar cuál sería el valor de la derivada direccional
- tener en cuenta que hay un valor máximo conocido para las derivadas direccionales en un punto
- Cuarto apartado
- hallar cuál sería el valor de la derivada direccional
- buscar la dirección que corresponde a ese valor de la derivada direccional