La integral definida puede utilizarse para calcular el volumen de sólidos que respondan a ciertas reglas de generación. Es el caso de los sólidos que tienen una sección transversal conocida.

 

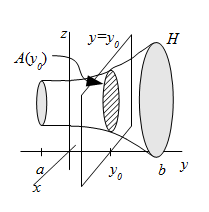
Supongamos por ejemplo que el sólido $H$ cumple que la sección transversal perpendicular al eje $0Y$ tiene área conocida: para cada $y_0\in[a,b]$, sea $A(y_0)$ el área de la sección de $H$ para el plano $y=y_0$. Entonces el volumen de $H$ viene dado por

\begin{equation}\mbox{Volumen}=\int_a^b A(y)\, dy\end{equation}

Obtención de esta fórmula.

 

Empezamos tomando una partición del intervalo $$[a,b]=\bigcup_{i=1}^n[y_{i-1},y_i]\ \ \ ,\ \ \ \Delta y_i=y_i-y_{i-1}$$ y llamando $\Delta V_i$ al volumen de la parte (podríamos decir ``rebanada'') de $H$ correspondiente al subintervalo $[y_{i-1},y_i]$, de forma que $$\mbox{volumen total}=\sum_{i=1}^n \Delta V_i$$ Ahora es preciso aproximar cada $\Delta V_i$. Para ello se utilizará el volumen de un cilindro. ¿Qué dimensiones va a tener este cilindro? Una claramente es $\Delta y_i=y_i-y_{i-1}$, pero ¿cuál es la base? La base del cilindro es la sección de $H$ correspondiente a $y=c_i$, siendo $c_i$ un punto intermedio a $y_{i-1}$ e $y_i$.

        

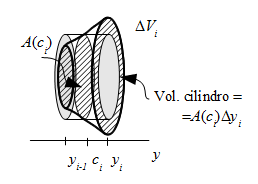
Así $$\mbox{volumen total}=\sum_{i=1}^n \Delta V_i \simeq \sum_{i=1}^n A(c_i)\Delta y_i$$ El segundo sumatorio es la suma de Riemann de la función $A(y)$ en $[a,b]$. Si converge para $n\longrightarrow \infty$, lo hace a la integral \begin{equation}\mbox{Volumen}=\int_a^b A(y)\, dy\end{equation}

 

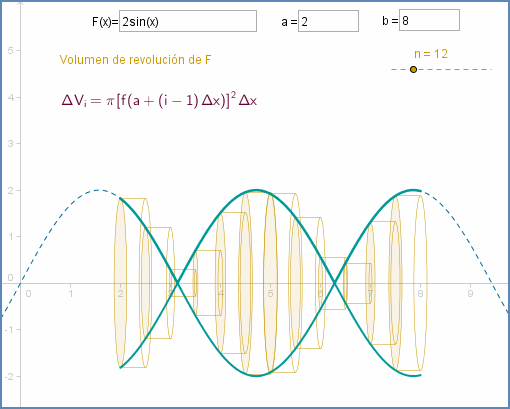
Ejemplo: Volumen de un sólido de revolución

 

Si consideramos que el sólido se genera al girar la curva $y=f(x)$ alrededor del eje X estando limitado por $x=a$ y $x=b$ el volumen del sólido será: $V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} $

 

Laboratorio: Volúmenes de revolución

 

 

Ejercicios interactivos:

• Volumen de sección conocida. Ejemplo 1
• Volumen de sección conocida. Ejemplo 2