Enunciado
Considera el cubo $$H=\{(x,y,z)/ \, 0\leq x\leq 1, \ 0\leq y\leq 1,\ 0\leq z\leq 1\}$$ la función
$$f(x,y,z)=x^3y^2z-xy\sqrt{z}$$ y el número $$I=\int\!\!\int\!\! \int_H f(x,y,z)\, dV$$
- Sin hallar $I$, encuentra $m$ y $M$ tales que $m\leq I\leq M$.
- Dibuja varias secciones de la caja $H$ coloreadas según la función $f(x,y,z)$.
- Comprueba el resultado del primer apartado hallando $I$, a mano y en el ordenador.
Resolución del primer apartado
Debemos recurrir a las propiedades de la integral triple, en particular a la propiedad de acotación. Puesto que el volumen de $H$ es 1, en este caso tendremos que $$m\leq I\leq M$$ si tomamos $m$ y $M$ cotas inferior y superior de $f$ en $H$, respectivamente. Para hallar esas cotas buscaremos el máximo y el mínimo de la función en $H$. Para encontrar el máximo, basta observar que la función nunca es positiva en $H$, pues $x^3y^2z$ es en todos los puntos de $H$ menor o igual que $xy\sqrt{z}$; esto lo sabemos porque al estar $x$, $y$ y $z$ entre 0 y 1,
$$x^3\leq x,\hspace{.3cm} y^2\leq y, \hspace{.3cm} z\leq \sqrt{z}$$
En el origen, por ejemplo, la función se anula, de donde deducimos que el máximo de $f$ en $H$ vale 0. Para hallar el mínimo tenemos que recurrir al cálculo diferencial, buscando los posibles extremos en el conjunto abierto y luego en la frontera.
- Analizamos si el gradiente de $f$ se anula en el interior de $H$. Hazlo tú y pulsa en 'Ver'.
Ver
Es fácil ver que $f'_x=3x^2y^2z-y\sqrt{z}$ y $f'_y=2x^3yz-x\sqrt{z}$ no se anulan simultáneamente en el interior de $H$, pues allí $x\neq 0$ e $y\neq 0$. Así pues no hay ningún punto crítico en el interior de $H$.
- En las caras $x=0$, $y=0$ y $z=0$, la función vale siempre 0.
- En la cara $z=1$, la función vale $$f(x,y,1)=x^3y^2-xy$$ Rápidamente se observa que las derivadas parciales de esta función no se anulan simultáneamente (en $0<x<1$, $0<y<1$)
- En la cara $y=1$, la función vale $$f(x,1,z)=x^3z-x\sqrt{z}$$ También podemos ver que para $0<x<1$, $0<z<1$, las derivadas parciales de esta función no se anulan simultáneamente
- En la cara $x=1$, la función es $$f(1,y,z)=y^2z-y\sqrt{z}=g(y,z)$$ cuyo gradiente $\ldots$
No se anula en $0<y<1$, $0<z<1$
Se anula en todos los puntos $0<y<1$, $0<z<1$
Se anula en los puntos de la curva $y=1/(2\sqrt{z})$
No es cierto, sí se anula en algún punto.
No se anula en todos.
En efecto, $(g'_y,g'_z)=(2yz-\sqrt{z},y^2-y/(2\sqrt{z}))$ se anula en esos puntos. En ellos la función vale $$f(1,\frac{1}{2\sqrt{z}},z)=-\frac{1}{4}$$
- En la arista $x=1$, $y=1$ la función vale $$f(1,1,z)=z-\sqrt{z}$$ que tiene un mínimo en $z=1/4$, donde la función vale $-1/4$.
- En la arista $x=1$, $z=1$ la función vale $$f(1,y,1)=y^2-y$$ que tiene un mínimo en $y=1/2$, donde la función vale también $-1/4$.
- En la arista $y=1$, $z=1$ la función vale $$f(x,1,1)=x^3-x$$ que tiene un mínimo en $x=1/\sqrt{3}$ de valor $$f(\frac{1}{\sqrt{3}},1,1)=-\frac{2}{9}\sqrt{3}$$
- En todos los vértices la función vale 0
Resolución del segundo apartado
Para dibujar unas secciones de la caja $H=[0,1]\times[0,1]\times[0,1]$ coloreadas según la función $f$, seguiremos los siguientes pasos (pulsa en continuar cuando hayas completado cada uno)- genera una malla de puntos en la caja $H$, llámala $[X,Y,Z]$
[X,Y,Z]=meshgrid(0:.05:1);
- genera una matriz, $F$, con los valores de f sobre los puntos de la malla $[X,Y,Z]$
F=X.^3.*Y.^2.*Z-X.*Y.*Z.^(1/2);
- ahora debemos elegir qué secciones queremos dibujar; por ejemplo si seleccionamos las secciones $x=.2$, $x=.4$, $x=.6$, $x=.8$, $y=.2$, $y=.4$, $y=.6$, $y=.8$, $z=.2$, $z=.4$, $z=.6$, y $z=.8$, debemos definir un vector con los valores $.2$, $.4$, $.6$ y $.8$. Llámalo $secc$.
secc = .2:.2:.8;
- utiliza el comando slice para dibujar esas secciones coloreadas
slice(X,Y,Z,TM,secc,secc,secc)
- por último, podemos etiquetar los ejes,
xlabel('x');ylabel('y');zlabel('z')
Ejecutando estas líneas obtendremos la siguiente figura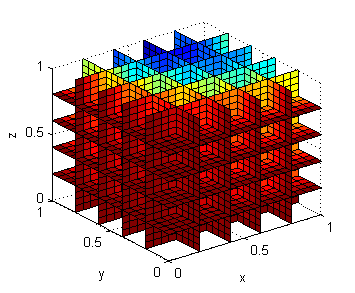
donde se adivina la situación de valores menores en las caras $x=0$ e $y=0$. Podemos girarla para ver la cara $y=1$, y las proximidades del punto donde se alcanza el mínimo, con
view([140,30])veremos
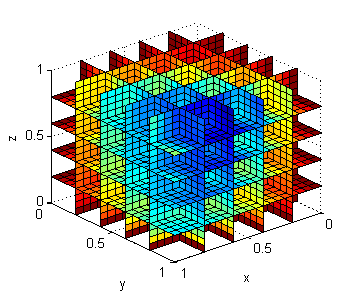
Resolución del tercer apartado
En este caso, esta integral es fácil de hallar a mano, haciendo las correspondientes integrales iteradas. Calcula $I$ y pulsa en 'Ver'.
Ver
$$I=\int_0^1\int_0^1\int_0^1 (x^3y^2z-xy\sqrt{z})\, dx\, dy\, dz=
\int_0^1 \int_0^1\left[\frac{1}{4}x^4y^2z-\frac{1}{2}x^2y\sqrt{z}\right]_0^1\, dy\, dz=$$
$$=\int_0^1 \int_0^1\left[\frac{1}{4}y^2z-\frac{1}{2}y\sqrt{z}\right]_0^1\, dy\, dz=
\int_0^1 \left[ \frac{1}{12}y^3z-\frac{1}{4}y^2\sqrt{z}\right]_0^1\, dz=$$
$$=\int_0^1 \left[ \frac{1}{12}z-\frac{1}{4}\sqrt{z}\right]_0^1\, dz=
\left.\frac{1}{24}z^2-\frac{1}{6}z\sqrt{z}\right]_0^1=-\frac{1}{8}$$
Podemos comprobar este resultado en el ordenador, poniendo
syms x y z I= int(int(int(x^3*y^2*z-x*y*sqrt(z),z,0,1),y,0,1),x,0,1)Observamos que las cotas encontradas en el primer apartado son correctas, pues $$-\frac{2}{9}\sqrt{3}< -\frac{1}{8}< 0$$