Enunciado
Un alambre se sitúa tomando la forma y ecuaciones de la curva espacial
$$C: \hspace{.3cm} x(t)=t\cos t \hspace{.2cm} , \hspace{.2cm} y(t)=t\, \mbox{sen}\, t\hspace{.2cm} , \hspace{.2cm} z(t)=\frac{t}{2} \hspace{.2cm} , \hspace{.3cm} t\in[\frac{\pi}{2},\frac{13\pi}{2}]$$
- Dibuja el alambre en el ordenador.
- Halla su longitud.
- Calcula la temperatura media, $T_m$, de los puntos del alambre si en cada punto la temperatura viene dada por $$T(x,y,z)=\frac{1}{\sqrt{\frac{5}{4}+x^2+y^2}}$$
- Encuentra el o los puntos del alambre donde se alcanza esa temperatura media y márcalos en tu dibujo.
- Se modifica el alambre, cortando una de sus vueltas, de manera que toma la forma de la curva $C^*=C_1\cup L\cup C_2$ donde:
- $C_1$: arco de $C$ para $t\in[\frac{\pi}{2},\frac{5\pi}{2}]$
- $L$: segmento recto en el plano $x=0$ entre los puntos $P_2(0, \frac{5\pi}{2},\frac{5\pi}{4})$ y $P_3(0, \frac{9\pi}{2},\frac{9\pi}{4})$
- $C_2$: arco de $C$ para $t\in[\frac{9\pi}{2},\frac{13\pi}{2}]$
Repite los apartados anteriores para este nuevo alambre.
- El campo vectorial del flujo de calor es ${\bf T}=\nabla T$. ¿Cuánto vale la integral de ${\bf T}$ a la largo de $C$? ¿y a lo largo de $C^*$?
- $C_1$: arco de $C$ para $t\in[\frac{\pi}{2},\frac{5\pi}{2}]$
- $L$: segmento recto en el plano $x=0$ entre los puntos $P_2(0, \frac{5\pi}{2},\frac{5\pi}{4})$ y $P_3(0, \frac{9\pi}{2},\frac{9\pi}{4})$
- $C_2$: arco de $C$ para $t\in[\frac{9\pi}{2},\frac{13\pi}{2}]$
Resolución del primer apartado
Para dibujar esta curva en el ordenador, definiremos un vector de parámetros sobre el que definir las coordenadas $x$, $y$ y $z$ para trazar la curva. Inténtalo y pulsa en 'Ver' cuando lo tengas.
Ver
t=pi/2:pi/20:13*pi/2; % vector de parámetros plot3(t.*cos(t),t.*sin(t),t/2) % trazado de la curva grid on
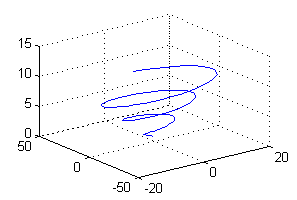
Se trata de una curva en forma de hélice, en la que los puntos se alejan del eje $0Z$ a medida que crece el valor de $t$; de hecho, todos los puntos de la curva están en el cono $z=\frac{1}{2}\sqrt{x^2+y^2}$.
Resolución del segundo apartado
Recordamos cómo se calcula la longitud de una curva. El elemento diferencial de arco de $C$ es
$(dx,dy,dz)=((\cos t-t\, \mbox{sen}\, t)\, dt, (\cos t+t\, \mbox{sen}\, t)\, dt,dt/2)$
$ds=\sqrt{\frac{5}{4}+t^2}$
Ninguna de las propuestas es correcta
No, eso es lo que solemos denotar por $d{\bf r}$ y se utiliza para encontrar la integral de línea de un campo vectorial a lo largo de una curva.
Cuidado, falta algo importante.
En efecto, ya que el elemento diferencial de arco de $C$ es $$ds=\sqrt{\frac{5}{4}+t^2}\, dt$$
Ahora puedes plantear la integral que da el valor de la longitud de $C$.
Pulsa en 'Continuar' cuando la hayas planteado.
$$\mbox{longitud}(C)=\int_C ds=\int_{\pi/2}^{13\pi/2} \sqrt{\frac{5}{4} +t^2}\, dt$$
Para calcular a mano esta integral podemos hacer el cambio de variable $$t=\frac{\sqrt{5}}{2}\,\mbox{Sh}\, u$$ que la convierte en $$\frac{5}{8}\int_{u_1}^{u_2} \mbox{Ch}^2u \, du=\frac{5}{8}\int_{u_1}^{u_2} (1+\mbox{Ch}\, 2u)\, du$$
siendo $u_1=\mbox{ArgSh}\, \frac{\pi}{\sqrt{5}}$ y $u_2=\mbox{ArgSh}\, \frac{13\pi}{\sqrt{5}}$,
de donde
$$\mbox{longitud}(C)=\frac{5}{8}\left[u+\frac{1}{2}\mbox{Sh}\, 2u\right]_{u_1}^{u_2}$$
Para terminar este cálculo y tener una expresión decimal para la longitud utilizamos el ordenador o la calculadora,
$$\mbox{longitud}(C)=208.8296$$
Otra opción es hacer uso del ordenador desde el principio del cálculo de la integral, poniendo
syms u longitud=double(int(sqrt(5/4+u^2),u,pi/2,13*pi/2))
Resolución del tercer apartado
Una de las aplicaciones de la integral de línea de un campo escalar es el cálculo de la temperatura media de un alambre. La longitud ya la tenemos calculada en el apartado anterior, así que falta hallar la integral de la temperatura a lo largo de $C$: $$I=\int_C T(x,y,z)\, ds=\int_{\pi/2}^{13\pi/2} T(x(t),y(t),z(t))\, \sqrt{\frac{5}{4} +t^2}\, dt $$ Encuentra $T(x(t),y(t),z(t))$ y realiza la integral simple (en este caso es inmediata). Pulsa en 'Ver' cuando lo tengas.
Ver
$$T(x(t),y(t),z(t))=\frac{t}{2\sqrt{\frac{5}{4}+t^2}}\hspace{.5cm}\Rightarrow\hspace{.5cm} I=\frac{1}{2}\int_{\pi/2}^{13\pi/2} t\, dt=\frac{21}{2}\pi^2$$
Por tanto, la temperatura media del alambre es
$$T_m=\frac{21\pi^2/2}{\mbox{longitud}(C)}=0.4962$$
Resolución del cuarto apartado
Se trata ahora de localizar el punto, o los puntos, del alambre que están a temperatura media. Esos puntos deben cumplir que $$T(x(t),y(t),z(t))=\frac{t}{2\sqrt{\frac{5}{4}+t^2}}=T_m$$ Las soluciones posibles de esta ecuación son
dos valores de $t$, que son: $t_m=\pm \frac{\sqrt{5} T_m}{\sqrt{1-4T_m^2}}$
Ninguna de las propuestas es correcta
sólo un valor de $t$: $t_m=\frac{\sqrt{5} T_m}{\sqrt{1-4T_m^2}}$
No, $t$ no toma valores negativos
Sí hay una correcta
Claro, puesto que $t$ no toma valores negativos
Luego sólo hay un punto a temperatura media, que es
$$P(x(t_m),y(t_m),z(t_m))$$
podemos añadirle al dibujo de la curva, poniendo
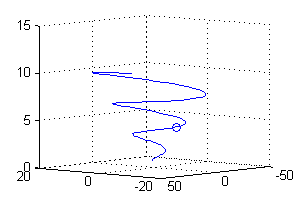
syms u longitud=double(int(sqrt(5/4+u^2),u,pi/2,13*pi/2)); Tm=21*pi^2/2/longitud; tm=sqrt(5)*Tm/sqrt(1-4*Tm^2); hold on plot3(tm*cos(tm),tm*sin(tm),tm/2,'o') % para dibujar el punto donde se alcanza la temp. media hold off

Resolución del quinto apartado
-
Dibujamos la curva $C^*=C_1\cup L\cup C_2$ donde:
- $C_1$: arco de $C$ para $t\in[\frac{\pi}{2},\frac{5\pi}{2}]$
- $L$: segmento recto en el plano $x=0$ entre los puntos $P_2(0, \frac{5\pi}{2},\frac{5\pi}{4})$ y $P_3(0, \frac{9\pi}{2},\frac{9\pi}{4})$
- $C_2$: arco de $C$ para $t\in[\frac{9\pi}{2},\frac{13\pi}{2}]$
t=[pi/2:pi/10:5*pi/2 9*pi/2:pi/10:13*pi/2]; % vector de parámetros plot3(t.*cos(t),t.*sin(t),t/2) % trazado de la curva grid on
En realidad le estamos dando para dibujar únicamente los puntos de los arcos $C_1$ y $C_2$; el tramo $L$, al ser un segmento recto queda dibujado al unir el último punto de $C_1$ con el primero de $C_2$: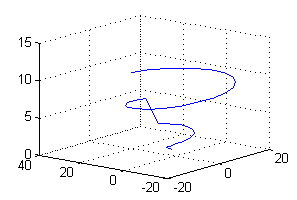
- Calculamos la longitud de $C^*$: utilizaremos el ordenador para hallar las longitudes de los arcos $C_1$ y $C_2$ y luego le sumaremos la longitud del segmento $L$. Inténtalo tú y pulsa en 'Ver'.
Ver
La longitud del segmento $L$ es $$|P_2P_3|=|(0,2\pi,\pi)|=\sqrt{5}\pi$$ y las de $C_1$ y $C_2$ las calculamos buscando la primitiva y evaluando en los extremos; por supuesto también sería válido hacer las dos integrales definidas correspondientes:
syms u fl=int(sqrt(1+a^2+u^2),u); longitud=double(subs(fl,u,5*pi/2)-subs(fl,u,pi/2)+sqrt(5)*pi+subs(fl,u,13*pi/2)-subs(fl,u,9*pi/2))Tras ejecutar estas líneas sabemos que la longitud es $${\bf longitud}(C^*)=146.4009$$
- La integral a lo largo de $C^*$ de la temperatura es
$\int_{\pi/2}^{13\pi/2} \frac{t}{2}\, dt$
la propuesta no es correcta
No, porque sobre el segmento $L$ la función $T(x(t),y(t),z(t))$ no es $t/2$
En efecto, sobre el segmento $L$ la función temperatura no es $t/2$; para hallar la forma correcta debemos parametrizar $L$ y luego ya sustituir en la expresión de $T(x,y,z)$. Hazlo tú y pulsa en 'Continuar'.
Una parametrización sencilla es tomar
$$L: \hspace{.4cm} x=0 ,\hspace{.3cm} y=\frac{5\pi}{2}+2\pi t,\hspace{.3cm} z=\frac{5\pi}{4}+\pi t,\hspace{.4cm} t\in[0,1]$$
La función temperatura sobre los puntos de $L$ es
$$T(x(t),y(t),z(t))=\pi\frac{5+4t}{4\sqrt{\frac{5}{4}+(\frac{5\pi}{2}+2\pi t)^2}}$$
La utilizamos para calcular la integral de la temperatura sobre la curva:
int1=double(int(u/2,u,pi/2,5*pi/2)); int2=double(int(u/2,u,9*pi/2,13*pi/2)); int3=double(sqrt(5)*pi^2*int((5/4+u)/sqrt(5/4+(5*pi/2+2*pi*u)^2),u,0,1)); integral=int1+int2+int3
-
La temperatura media puede ser calculada ahora fácilmente con
Tm=integral/longitud
Tm= 0.4958y el punto $P(x,y,z)$ que está a la temperatura $T_m$ debe cumplir que $$z=T_m\sqrt{\frac{5}{4}+x^2+y^2}$$ Si fuera un punto del arco $C_1$ o del $C_2$, el valor $t_m$ del parámetro tendría que cumplir que $$t_m=\frac{\sqrt{5} T_m}{\sqrt{1-4T_m^2}}$$
Eso puede darse así
Eso no puede darse así
No, pues $\frac{\sqrt{5} T_m}{\sqrt{1-4T_m^2}}=8.5327$, que no está ni en $[\pi/2,5\pi/2]$ ni en $[9\pi/2,13\pi/2]$
En efecto, pues $\frac{\sqrt{5} T_m}{\sqrt{1-4T_m^2}}=8.5327$, que no está ni en $[\pi/2,5\pi/2]$ ni en $[9\pi/2,13\pi/2]$. Eso significa que el punto donde se alcanza la temperatura media está en el segmento $L$, búscalo y pulsa en 'Continuar'.
Debemos igualar $T_m$ a la expresión de la función temperatura sobre el segmento $L$:
$$\pi\frac{5+4t}{4\sqrt{\frac{5}{4}+(\frac{5\pi}{2}+2\pi t)^2}}=T_m$$
Elevando al cuadrado, tendremos que
$$(5+4t)^2=\frac{16}{\pi^2}T_m^2\left(\frac{5}{4}+(\frac{5\pi}{2}+2\pi t)^2\right)$$
Esta ecuación se puede resolver a mano (es una ecuación polinómica de grado 2), pero si queremos ahorrarnos cuentas utilizaremos el ordenador. Ejecutando (se supone que $u$ ya está declarada antes como simbólica)

r=double(solve((5+4*u)^2-16*Tm^2*(5/4+(5*pi/2+2*pi*u)^2)/pi^2)) % vector con las dos solucionesobtendremos dos raíces, pero sólo una es positiva: $$r= 0.1080$$ El punto del segmento $L$ correspondiente a ese valor del parámetro está a temperatura $T_m$. Podemos calcular sus coordenadas y marcar su situación sobre la curva $C^*$, añadiendo las siguientes líneas:
coordy=5*pi/2+2*pi*r(2); % la solución válida de la ecuación anterior es r(2) p=[0, coordy ,coordy/2] hold on plot3(0, coordy ,coordy/2,'o') hold offobtendremos que el punto es $P(0,8.5327,4.2663)$ y la figura resultante es

Resolución del sexto apartado
El campo vectorial flujo de calor es el gradiente de la temperatura: ${\bf T}=\nabla T$. En la siguiente figura puedes ver una muestra de este campo vectorial sobre puntos de la curva $C$; en ella se aprecia que la dirección de estos vectores es muy diferente a la dirección tangente a la curva, lo que hace preveer que la integral debe darnos un valor cercano al cero: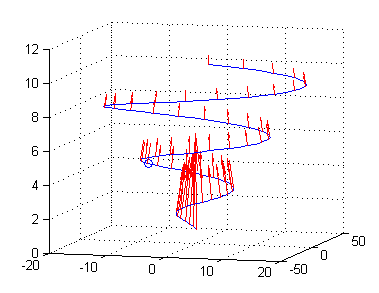
En este apartado debemos hallar la integral de ${\bf T}$ a la largo de las curvas $C$ y $C^*$. Para ello
Hallaremos el gradiente de $T$, lo evaluaremos sobre las curvas, lo multiplicaremos por los $d{\bf r}$ y calcularemos las integrales
Ninguna de las propuestas es adecuada
Utilizaremos el teorema fundamental de integrales de línea
Eso es correcto y viable, pero es mucho menos trabajoso utilizar otro método
Sí hay una propuesta adecuada
En efecto, lo mejor en este caso, puesto que se trata de un campo vectorial gradiente, es utilizar el teorema fundamental de integrales de línea. Comprueba que se cumplen las condiciones y utilízalo; pulsa en 'Continuar' cuando lo tengas.
El punto inicial de $C$ es $P_1(0,\frac{\pi}{2},\frac{\pi}{4})$ y el final es $P_4(0,13\frac{\pi}{2},13\frac{\pi}{4})$, luego
$$\int_C {\bf T}\cdot d{\bf r}= T(P_4)-T(P_1)=\frac{13\pi}{4\sqrt{\frac{5}{4}+169\frac{\pi^2}{4}}}-\frac{\pi}{4\sqrt{\frac{5}{4}+\frac{\pi^2}{4}}}=0.0919$$
Puesto que los puntos inicial y final de $C^*$ son los mismos, sabemos que
$$\int_{C^*} {\bf T}\cdot d{\bf r}=\int_C {\bf T}\cdot d{\bf r}$$