Enunciado
- Halla la transformada inversa de Laplace de la función $$F(s)=\frac{e^{-3s}}{s^2+8s+20}$$
- Idem para la función $$G(s)=\frac{s}{s^2+8s+20}$$
- Sabiendo que ${\cal L}[\delta(t)]=1$, encuentra la solución del siguiente problema de valor inicial
$$x''(t)+8x'(t)+20x(t)=\delta(t-3)\ \ , \ \ x(0)=1\ , \ \ x'(0)=-8$$
¿Cuánto vale $x(\pi/2)$? ¿Cuánto vale $x(\pi)$?
- Representa la función $x(t)$ del apartado anterior para $t\in[0,4]$ y marca sobre su gráfica los puntos correspondientes a $t=\pi/2$ y a $t=\pi$.
Resolución primer apartado
Paso 1
Observar que la función $F(s)$ contiene un factor de la forma $e^{-cs}$ y recordar la propiedad de traslación en la variable $t$. Para aplicar esta propiedad debemos encontrar previamente la transformada inversa de $$\frac{1}{s^2+8s+20}$$ Completaremos cuadrados en el polinomio $s^2+8s+20$ y utilizaremos una de las transformadas de la tabla básica junto con la propiedad de traslación en la variable $s$... hazlo tú y pulsa en 'Ver'.
Ver
$$s^2+8s+20=(s+4)^2+4 \hspace{.4cm} \Rightarrow \hspace{.4cm} \frac{1}{s^2+8s+20}=\frac{1}{(s+4)^2+2^2}$$
Puesto que
$${\cal L}[\frac{1}{2}\mbox{sen} 2t]=\frac{1}{s^2+2^2}$$
en base a la propiedad de traslación en la variable $s$,
$$\frac{1}{(s+4)^2+2^2}={\cal L}[\frac{e^{-4t}}{2}\mbox{sen} 2t]$$
Paso 2
Utilizar la transformada inversa de $\frac{1}{(s+4)^2+2^2}$ para hallar la de $F(s)=\frac{e^{-3s}}{s^2+8s+20}$. Aquí es donde interviene la propiedad de traslación en el tiempo; en base a esa propiedad,
$${\cal L}^{-1}[\frac{e^{-3s}}{s^2+8s+20}]=\frac{1}{2}U(t-3)e^{-4t}\mbox{sen} 2t$$
$${\cal L}^{-1}[\frac{e^{-3s}}{s^2+8s+20}]=\frac{1}{2}U(t+3)e^{-4(t+3)}\mbox{sen} 2(t+3)$$
$${\cal L}^{-1}[\frac{e^{-3s}}{s^2+8s+20}]=\frac{1}{2}e^{-4(t-3)}\mbox{sen} 2t$$
$${\cal L}^{-1}[\frac{e^{-3s}}{s^2+8s+20}]=\frac{1}{2}e^{-4(t-3)}\mbox{sen} 2(t-3)$$
Ninguna de las opciones presentadas es correcta.
Debes trasladar la función, no sólo añadirle el factor en $U(t)$.
Cuidado con el signo.
No es correcto, vuelve a mirar la propiedad.
Debes anular la función a la izquierda de $t=c$, en este caso $t=3$.
En efecto, ninguna de las propuestas es correcta, ya que
$$f(t)={\cal L}^{-1}[\frac{e^{-3s}}{s^2+8s+20}]=\frac{1}{2}U(t-3)e^{-4(t-3)}\cos 2(t-3)$$
Resolución del segundo apartado
El objetivo de este apartado es encontrar $$g(t)={\cal L}^{-1}[G(s)]={\cal L}^{-1}[\frac{s}{s^2+8s+20}]$$ Del apartado anterior sabemos que $s^2+8s+20=(s+4)^2+4$, y puesto que ${\cal L}[\cos 2t]=\frac{s}{s^2+4}$, en base a la propiedad de traslación en la variable s
${\cal L}^{-1}[\frac{s}{s^2+8s+20}]=e^{-4t}\cos 2t$
${\cal L}^{-1}[\frac{s}{s^2+8s+20}]=U(t-4)e^{-4(t-4)}\cos 2(t-4)$
Ninguna de las opciones presentadas es correcta.
No es correcto, pues no estás teniendo en cuenta que aunque el denominador se escriba en función de $s+4$ (pues es $(s+4)^2+4$) el numerador todavía no está puesto en función de $s+4$.
Parece que estás mezclando varias propiedades.
En efecto, ninguna es correcta. Antes de aplicar la propiedad de traslación hemos de escribir TODA la función en términos de $s+4$. Hazlo tú y aplica después correctamente la propiedad; pulsa en 'Continuar' cuando tengas de inversa de $G(s)$.
$$\frac{s}{s^2+8s+20}=\frac{s}{(s+4)^2+4}=\frac{s+4}{(s+4)^2+4}-\frac{4}{(s+4)^2+4}$$
El primer factor de esta resta es la traslación de 4 unidades en $s$ de la función $\frac{s}{s^2+4}$ y el segundo es la misma traslación pero de
$\frac{4}{s^2+4}$, luego
$$\frac{s}{s^2+8s+20}={\cal L}[e^{-4t}(\cos 2t-2\mbox{sen}\, 2t)]$$
o lo que es lo mismo,
$$g(t)={\cal L}^{-1}[G(s)]={\cal L}^{-1}[\frac{s}{s^2+8s+20}]=e^{-4t}(\cos 2t-2\mbox{sen}\, 2t)$$
Resolución del tercer apartado
En este apartado se halla la solución $x(t)$ del problema $$x''(t)+8x'(t)+20x(t)=\delta(t-3)\ \ , \ \ x(0)=1\ , \ \ x'(0)=-8$$ y en particular se calculan los valores $x(\pi/2)$ y $x(\pi)$.Paso 1
Transformar la ecuación diferencial en una ecuación algebraica en la incógnita $X(s)={\cal L}[x]$. Para ello utilizamos, además de la transformada de $\delta(t)$, las propiedades de linealidad de la transformada, traslación en la variable $t$ y transformada de la derivada. Comenzamos encontrando la transformada del segundo término, $\delta(t-3)$:
$${\cal L}[\delta(t-3)]=e^{-3t}$$
$${\cal L}[\delta(t-3)]=3s$$
Ninguna de las propuestas es correcta.
$${\cal L}[\delta(t-3)]=e^{-3s}$$
¡Cuidado con el nombre de la variable!
¿De dónde sale eso?
Sí hay una propuesta correcta.
En efecto, esa es la función correcta.
Transforma ahora el primer término de la ecuación, $$x''(t)+8x'(t)+20x(t)=\delta(t-3)$$ teniendo en cuenta que $x(0)=1$ y $x'(0)=-8$:
$$s^2X(s)+8s-1+8sX(s)-1+20X(s)=e^{-3s} \hspace{.4cm} \Rightarrow \hspace{.4cm} X(s)(s^2+8s+20)+8s-1=e^{-3s}$$
$$s^2X(s)+8s-1+8sX(s)-1+20X(s)=e^{-3s} \hspace{.4cm} \Rightarrow \hspace{.4cm} X(s)(s^2+8s+20)+8s-2=e^{-3s}$$
$$s^2X(s)-s+8+8sX(s)-8+20X(s)=e^{-3s} \hspace{.4cm} \Rightarrow \hspace{.4cm} X(s)(s^2+8s+20)-s=e^{-3s}$$
No es correcto, revísalo.
No es correcto, revísalo.
En efecto, con lo cual
$$X(s)=\frac{s+e^{-3s}}{s^2+8s+20}$$
Paso 2
Hallar la función $x(t)={\cal L}^{-1}[X(s)]$. Este paso ya está resuelto, pues debido a la linealidad, $$x(t)={\cal L}^{-1}[\frac{s}{s^2+8s+20}]+{\cal L}^{-1}[\frac{e^{-3s}}{s^2+8s+20}]$$ que son las transformadas inversas calculadas en los dos apartados anteriores de este ejercicio: $$x(t)=e^{-4t}(\cos 2t-2\mbox{sen}\, 2t)+\frac{1}{2}U(t-3)e^{-4(t-3)}\mbox{sen}\, 2(t-3)$$Paso 3
¿Cuánto vale $x(t)$ para $t=\pi/2$ y para $t=\pi$? Únicamente hemos de sustituir en la expresión de la función y tener en cuenta cómo se define la función $U(t)$. Encuentra esos dos valores y pulsa en 'Ver'.
Ver
- Puesto que $U(\pi/2-3)=0$ (por ser $\pi/2-3<0$) $$x(\frac{\pi}{2})=-e^{-2\pi}\approx -0.0019$$
- Puesto que $U(\pi-3)=1$ (por ser $\pi-3>0$) $$x(\pi)=e^{-4\pi}+\frac{1}{2}e^{-4(\pi-3)}\mbox{sen}\, 2(\pi-3)=e^{-4\pi}(1-\frac{e^{12}}{2}\mbox{sen}\, 6)\approx 0.0793$$
Resolución del cuarto apartado
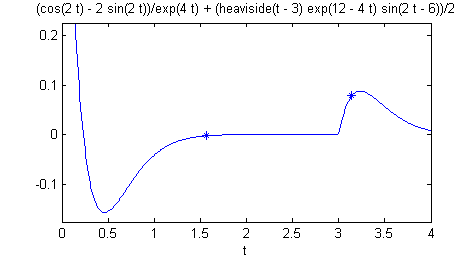
Para representar la función $$x(t)=e^{-4t}(\cos 2t-2\mbox{sen}\, 2t)+\frac{1}{2}U(t-3)e^{-4(t-3)}\mbox{sen}\, 2(t-3)$$ podemos recurrir a la función predefinida 'heaviside(t)', de manera quesyms t x=exp(-4*t)*(cos(2*t)-2*sin(2*t))+heaviside(t-3)*exp(-4*(t-3))*sin(2*(t-3))/2; ezplot(x,[0,4])nos dará la representación de la solución. Para representar sobre ella los dos puntos requeridos, a las líneas anteriores añadiremos
hold on v=subs(x,t,[pi/2 pi]) plot([pi/2 pi],v,'*') hold offLa figura que resulta es