Enunciado
- Encuentra la transformada de Laplace de la función $$f(t)=\left\{\begin{array}{rrr} 1 & , & 0 <t<3 \\ -2 & , & 3<t<4 \\ 0 & , & \mbox{si no} \end{array}
\right.$$
utilizando la transformada de $U(t)$ y la propiedad de traslación.
- Aplica transformadas de Laplace para resolver el siguiente sistema diferencial:
$$\left\{\begin{array}{lll} x'(t)=y(t)-f(t) & , & x(0)=0 \\ y'(t)=-x(t)+f(t) & , & y(0)=0 \end{array}
\right.$$
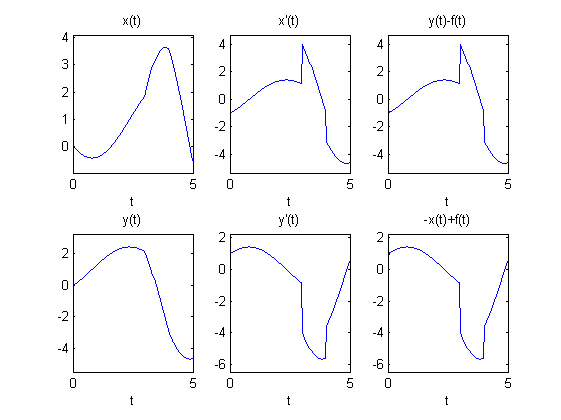
- Representa en el ordenador, disponiéndolas en una matriz de 2x3, las gráficas de $x(t)$, $x'(t)$, $y(t)-f(t)$, $y(t)$, $y'(t)$ y $-x(t)+f(t)$.
Resolución del primer apartado
Paso 1
Debemos escribir la función $f(t)$ como una única expresión. Para ello nos valdremos de la función escalón unitario: $$U(t)=\left\{\begin{array}{lll} 0 & \mbox{si} & t<0 \\ 1 & \mbox{si} & t>0 \end{array} \right.$$ Puede ayudarnos hacer la representación de la función $f(t)$:
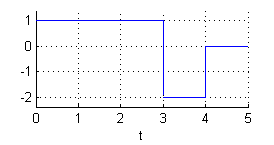
$f(t)=U(t)+U(t-3)+U(t-4)$
$f(t)=U(t)-3U(t+3)+2U(t+4)$
Ninguna de las presentadas es correcta.
$f(t)=U(t)-3U(t-3)+2U(t-4)$
Esa función vale 1 entre $t=0$ y $t=3$, vale 2 entre $t=3$ y $t=4$ y vale 3 a partir de $t=4$.
Esa funcion tendrá los saltos en $t=-3$ y $t=-4$.
Sí hay una correcta.
En efecto, en $t=0$ hay un salto de una unidad hacia arriba, en $t=3$ hay un salto de 3 unidades hacia abajo y en $t=4$ hay un salto de 2 unidades hacia arriba.
Paso 2
Ahora ya podemos aplicar la propiedad de traslación en la variable $t$ para hallar fácilmente la transformada de $f(t)$; utilizaremos únicamente la primera transformada de la tabla básica de transformadas. Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
$$f(t)=U(t)-3U(t-3)+2U(t-4) \hspace{.3cm} \Rightarrow \hspace{.3cm} F(s)={\cal L}[f(t)]=\frac{1}{s}(1-3e^{-3s}+2e^{-4s})$$
Resolución del segundo apartado
Paso 1
Aplicamos transformadas a ambos lados de cada una de las ecuaciones y utilizamos las propiedades de linealidad de la transformada y de la transformada de la derivada. Las dos ecuaciones se convierten en ... Hazlo tú y pulsa en 'Ver'.
Ver
La primera ecuación se convierte en $$sX(s)=Y(s)-F(s)$$ y la segunda en $$sY(s)=-X(s)+F(s)$$ formando el sistema
$$\left\{\begin{array}{l} sX(s)-Y(s)=-F(s) \\ X(s)+sY(s)=F(s)\end{array}\right.$$
Paso 2
Debemos resolver el sistema anterior en las funciones $X(s)$ e $Y(s)$: si por ejemplo multiplicamos la primera por $s$ y la sumamos con la segunda podremos fácilmente despejar $X(s)$; de la primera obtendremos después $Y(s)$. Pulsa en 'Ver' cuando la tengas.
Ver
Las funciones $X(s)$ e $Y(s)$ resultan
$$X(s)=\frac{1-s}{s^2+1}F(s) \hspace{.3cm} , \hspace{.3cm} Y(s)=\frac{s+1}{s^2+1}F(s)$$
o bien, teniendo en cuenta el resultado del primer apartado,
$$X(s)=\frac{1-s}{(s^2+1)s}(1-3e^{-3s}+2e^{-4s}) \hspace{.3cm} , \hspace{.3cm} Y(s)=\frac{s+1}{(s^2+1)s}(1-3e^{-3s}+2e^{-4s})$$
Paso 3
Por último han de encontrarse las funciones transformadas inversas de éstas, $$x(t)={\cal L}^{-1}[X(s)] \hspace{.6cm} \mbox{e} \hspace{.6cm} y(t)={\cal L}^{-1}[Y(s)]$$ Puesto que $$\frac{1-s}{(s^2+1)s}=\frac{1}{(s^2+1)s}-\frac{s}{(s^2+1)s}=\frac{1}{(s^2+1)s}-\frac{1}{s^2+1}$$ y $$\frac{s+1}{(s^2+1)s}=\frac{s}{(s^2+1)s}+\frac{1}{(s^2+1)s}=\frac{1}{s^2+1}+\frac{1}{(s^2+1)s}$$ y la transformada inversa de $\frac{1}{s^2+1}$ es conocida, debemos ocuparnos únicamente de calcular la del término $\frac{1}{(s^2+1)s}$. Para ello recurriremos a descomponerlo en fracciones simples:
$$\frac{1}{(s^2+1)s}=\frac{A}{s}+\frac{B}{s^2+1}$$
$$\frac{1}{(s^2+1)s}=\frac{A}{s}+\frac{B}{s+1}+\frac{C}{s-1}$$
Ninguna de las dos propuestas es correcta.
No es correcto, pues $s^2+1$ tiene grado 2, necesita un numerador de grado 1.
No, $s=-1$ y $s=1$ no son raíces de $s^2+1$.
En efecto, ninguna de las dos es correcta. Tendremos que escribir
$$\frac{1}{(s^2+1)s}=\frac{A}{s}+\frac{Bs+C}{s^2+1}$$
Halla los valores $A$, $B$ y $C$, encuentra $$g(t)={\cal L}^{-1}[\frac{1-s}{(s^2+1)s}]$$ y
$$h(t)={\cal L}^{-1}[\frac{s+1}{(s^2+1)s}]$$ y pulsa en 'Continuar'.
Puesto que
$$\frac{1}{(s^2+1)s}=\frac{1}{s}-\frac{s}{s^2+1}$$
y sabiendo que ${\cal L}^{-1}[\frac{1}{s}]=1$, ${\cal L}^{-1}[\frac{s}{s^2+1}]=\cos t$ y ${\cal L}^{-1}[\frac{1}{s^2+1}]=\mbox{sen}\, t$
tendremos
$$g(t)={\cal L}^{-1}[\frac{1-s}{(s^2+1)s}]=1-\cos t-\mbox{sen}\, t$$ y
$$h(t)={\cal L}^{-1}[\frac{s+1}{(s^2+1)s}]=1-\cos t+\mbox{sen}\, t$$
¿Cómo utilizamos ahora estas transformadas inversas para encontrar las de $X(s)$ e $Y(s)$? Recuerda que
$$X(s)=\frac{1-s}{(s^2+1)s}(1-3e^{-3s}+2e^{-4s}) \hspace{.3cm} , \hspace{.3cm} Y(s)=\frac{s+1}{(s^2+1)s}(1-3e^{-3s}+2e^{-4s})$$
Recurriendo a la propiedad de traslación en la variable $s$.
Ninguna de las dos propuestas es apropiada.
Recurriendo a la propiedad de traslación en la variable $t$.
Estas funciones de $s$ no presentan traslación en esa variable.
Sí hay una apropiada.
En efecto, ésa es la forma en que encontraremos las inversas de $X(s)$ e $Y(s)$.
Empezamos con la transformada inversa de $X(s)$,
$$x(t)={\cal L}^{-1}[X(s)]=g(t)U(t)-3g(t)U(t-3)+2g(t)U(t-4)$$
$$x(t)={\cal L}^{-1}[X(s)]=g(t)U(t)-3g(t)U(t+3)+2g(t)U(t+4)$$
Ninguna de las dos propuestas es apropiada.
No estás aplicando bien la propiedad, fíjate mejor.
No estás aplicando bien la propiedad, fíjate mejor en el signo.
En efecto, las dos tienen fallos. Lo correcto es
$$x(t)={\cal L}^{-1}[X(s)]=g(t)U(t)-3g(t-3)U(t-3)+2g(t-4)U(t-4)$$
y similarmente, para $Y(s)$,
$$y(t)={\cal L}^{-1}[Y(s)]=h(t)U(t)-3h(t-3)U(t-3)+2h(t-4)U(t-4)$$
Resumen primeros apartados
- Hallar la transformada de Laplace de la función $f(t)$ que aparece en los segundos términos de las ecuaciones del sistema diferencial (primer apartado)
- Aplicar transformadas a ambos lados de las dos ecuaciones.
- Utilizar las propiedades de linealidad y de la transformada de la derivada para encontrar el sistema de ecuaciones algebraico en las funciones transformadas.
- Resolver ese sistema.
- Hallar las transformadas inversas, utilizando descomposición en fracciones simples y la propiedad de traslación en la variable $t$.
Resolución del tercer apartado
Generaremos una matriz 2x3 con las gráficas de $x(t)$, $x'(t)$ e $y(t)-f(t)$ en la primera fila y las de $y(t)$, $y'(t)$ y $-x(t)+f(t)$ en la segunda. El intervalo elegido para la variable $t$ es $[0,5]$. Para ello, escribiremos en un fichero... (Vete introduciendo en el fichero las líneas correspondientes a cada tarea que se indica y luego pulsas en 'Continuar')- Declara la variable $t$ como simbólica y define las funciones $f(t)$, $g(t)$ y $h(t)$; para definir $f(t)$ has de utilizar la función 'heaviside(t)':
syms t f=heaviside(t)-3*heaviside(t-3)+2*heaviside(t-4); g=1-cos(t)-sin(t); h=1-cos(t)+sin(t);
- para representar la función $x(t)$, debemos definirla usando la función 'heaviside(t)' y también las funciones $g(t-3)$ y $g(t-4)$ que habremos de definir previamente sustituyendo (con el comando 'subs') $t$ por $t-3$ o por $t-4$ en la $g$ definida antes; después de definirla, represéntala en la primera celda de la primera fila, utilizando el comando 'ezplot':
%%% representación de x(t)
g3=subs(g,t,t-3); g4=subs(g,t,t-4);
x=g*heaviside(t)-3*g3*heaviside(t-3)+2*g4*heaviside(t-4);
subplot(2,3,1)
ezplot(x,[0,5])
title('x(t)')
- de igual forma genera la función $y(t)$ y represéntala en la primera celda de la segunda fila:
%%% representación de y(t)
h3=subs(h,t,t-3); h4=subs(h,t,t-4);
y=h*heaviside(t)-3*h3*heaviside(t-3)+2*h4*heaviside(t-4);
subplot(2,3,4)
ezplot(y,[0,5])
title('y(t)')
- utiliza el comando 'diff' para generar $x'(t)$ y represéntala en la segunda celda de la primera fila:
%%% representación de x'(t)
dx=diff(x);
subplot(2,3,2)
ezplot(dx,[0,5])
title('x''(t)')
- ahora haremos lo propio con $y'(t)$, posicionándola en la segunda celda de la segunda fila:
%%% representación de y'(t)
dy=diff(y);
subplot(2,3,5)
ezplot(dy,[0,5])
title('y''(t)')
- representa ahora, en la última celda de la primera fila de gráficas, la función $y(t)-f(t)$
%%% representación de y(t)-f(t)
subplot(2,3,3)
ezplot(y-f,[0,5])
title('y(t)-f(t)')
- y por último representa, en la última celda de la segunda fila de gráficas, la función $-x(t)+f(t)$
%%% representación de -x(t)+f(t)
subplot(2,3,6)
ezplot(-x+f,[0,5])
title('-x(t)+f(t)')
El resultado de ejecutar todas estas líneas es la figura