Enunciado
La función $f(x,y)$ es diferenciable en el punto $(3,1)$ del plano. Además, sabemos que $f(3,1)=2$ y que las derivadas direccionales de $f$ en $(3,1)$ respecto de las direcciones ${\bf u}=\frac{1}{\sqrt{2}}(1,-1)$ y ${\bf v}=\frac{1}{\sqrt{5}}(2,1)$ son $$D_{\bf u}f(3,1)=\sqrt{2} \ \ \ \mbox{y}\ \ \ D_{\bf v}f(3,1)=-1$$
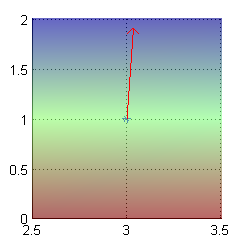
- Dibuja a mano y en el ordenador los vectores ${\bf u}=\frac{1}{\sqrt{2}}(1,-1)$ y ${\bf v}=\frac{1}{\sqrt{5}}(2,1)$ situados en el punto $(3,1)$. Halla y representa el vector gradiente de $f$ en $(3,1)$.
- Encuentra la ecuación del plano tangente a la superficie $z=f(x,y)$ en el punto $(3,1)$.
- Colocamos una bola en la superficie $z=f(x,y)$, en el punto correspondiente a las coordenadas $(3,1)$. ¿Hacia qué dirección cae la bola si la soltamos en ese punto? ¿Cuál será el vector tangente a su trayectoria? Dibuja ese vector y una porción de plano tangente que contenga al punto donde se suelta la bola.
- Ahora colocamos la bola no en la superficie sino en el plano tangente calculado antes. ¿Cuánta altura perdería la bola si avanzase 3 unidades de longitud desde el punto correspondiente a $(3,1)$ hacia el punto correspondiente a $(0,2)$? Dibuja el plano tangente y la trayectoria de la bola.
Resolución del primer apartado
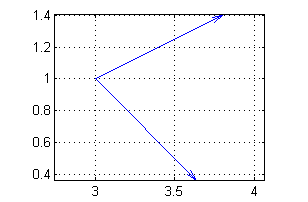
Para dibujar las direcciones ${\bf u}=\frac{1}{\sqrt{2}}(1,-1)$ y ${\bf v}=\frac{1}{\sqrt{5}}(2,1)$ situadas en el punto $(3,1)$ pondremos
Ahora hemos de calcular el vector gradiente.
quiver([3 3], [1 1], [1/sqrt(2) 2/sqrt(5)], [-1/sqrt(2) 1/sqrt(5)]) axis equal grid on

Ahora hemos de calcular el vector gradiente.
Paso 1
Para simplificar la escritura llamamos $$a=f'_x(3,1)\hspace{.2cm} , \hspace{.2cm} b=f'_y(3,1)$$ Sabemos cómo se escribe la derivada direccional de una función diferenciable utilizando el gradiente. Aplicando este resultado aquí, obtendremos un sistema de dos ecuaciones en las incógnitas $a$ y $b$. Encuentra ese sistema y pulsa en 'Ver' cuando lo tengas.
Ver
En efecto, con la derivada respecto de ${\bf u}=\frac{1}{\sqrt{2}}(1,-1)$, tenemos
$$D_{\bf u}f(3,1)=(a,b)\cdot {\bf u}=\frac{1}{\sqrt{2}}(a-b)=\sqrt{2}$$
y con la derivada respecto de ${\bf v}=\frac{1}{\sqrt{5}}(2,1)$,
$$D_{\bf v}f(3,1)=(a,b)\cdot {\bf v}=\frac{1}{\sqrt{5}}(2a+b)=-1$$
con lo cual
$$a-b=2\ \ \ \mbox{y}\ \ \ 2a+b=-\sqrt{5}$$
Paso 2
Resuelve este sistema y pulsa en 'Continuar'
La solución de este sistema es
$$a=\frac{2-\sqrt{5}}{3}\ \ ,\ \ b=-\frac{4+\sqrt{5}}{3}$$
Para dibujar el vector gradiente de $f$ en la misma figura que los anteriores, añadiremos las líneas
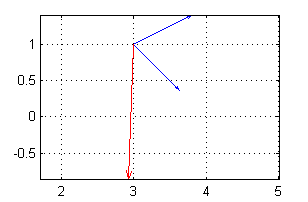
hold on quiver(3,1,(2-sqrt(5))/3,-(4+sqrt(5))/3,'r') hold off

Resolución del segundo apartado
El plano tangente contiene a todos los puntos $(x,y,z)$ que cumplan que el vector $(x-3,y-1,z-2)$ sea perpendicular al vector $(f'_x(3,1),f'_y(3,1),-1)$. Por tanto, en este caso es
$$3z=6+(\sqrt{5}-2)(x-3)+(4+\sqrt{5})(y-1)$$
$$\frac{2-\sqrt{5}}{3}(x-3)-\frac{4+\sqrt{5}}{3}(y-1)-z+2=0$$
No es correcto; comprueba los signos.
En efecto, esa es una expresión para el plano tangente, en la que podemos operar, obteniendo
$$3z=(2-\sqrt{5})x-(4+\sqrt{5})y+4(1+\sqrt{5})$$
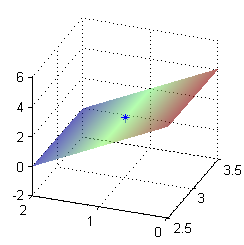

Resolución del tercer apartado
Una bola soltada en $(3,1,2)$ caerá en la dirección en la que la derivada direccional sea mínima. Por tanto, la dirección que toma la bola es la de $$-\nabla f=\left(\frac{\sqrt{5}-2}{3},\frac{4+\sqrt{5}}{3}\right)$$ En el punto $(3,1,2)$ el vector tangente a la trayectoria seguida por la bola es
$$\left(\frac{\sqrt{5}-2}{3},\frac{4+\sqrt{5}}{3},1\right)$$
$$\left(\frac{\sqrt{5}-2}{3},\frac{4+\sqrt{5}}{3},\frac{30+4\sqrt{5}}{9}\right)$$
$$\left(\frac{\sqrt{5}-2}{3},\frac{4+\sqrt{5}}{3},-\frac{\sqrt{30+4\sqrt{5}}}{3}\right)$$
Ninguna de las opciones presentadas es correcta
¿Por qué la tercera componente va a ser un $1$?
Revisa la tercera componente.
Cuidado con las dos primeras componentes. No son una dirección.
En efecto, no hay ninguna correcta. Si en la tercera componente ponemos el valor de la derivada direccional, en las dos primeras componentes debemos poner la dirección. El vector $-\nabla f$ nos marca la dirección, pero para que sea una dirección falta dividir cada componente por el módulo del vector. El vector tangente a la trayectoria es por tanto... hazlo tú y pulsa en 'Continuar'.
El vector tangente es
$$\left(\frac{\sqrt{5}-2}{3|\nabla f|},\frac{4+\sqrt{5}}{3|\nabla f|},-\nabla f\right)=\left(\frac{\sqrt{5}-2}{\sqrt{30+4\sqrt{5}}},\frac{4+\sqrt{5}}{\sqrt{30+4\sqrt{5}}},-\frac{\sqrt{30+4\sqrt{5}}}{3}\right)$$
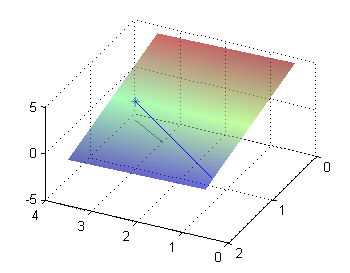
Para hacer la siguiente figura con una porción del plano tangente y el vector tangente a la trayectoria de la bola
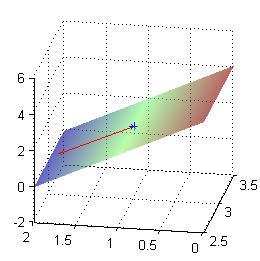
hemos utilizado el código

hemos utilizado el código
plot3(3,1,2,'*') % punto donde se suelta la bola [X,Y]=meshgrid(2.5:3.5,0:2); % malla para dibujar porción de plano hold on surf(X,Y,2+(2-sqrt(5))*(X-3)/3-(4+sqrt(5))*(Y-1)/3) % plano shading interp alpha(.6) view([-80,22]) grid on n=norm([(-2+sqrt(5))/3,(4+sqrt(5))/3]); % módulo del vector gradiente quiver3(3,1,2,(-2+sqrt(5))/(3*n),(4+sqrt(5))/(3*n),-n,'r') % vector tangente hold offTambién puede ser ilustrativo verlo desde arriba:

Resolución del cuarto apartado
Paso 1
En primer lugar hemos de encontrar la dirección (vector del plano de módulo $1$) que el enunciado marca para la bola: si se mueve desde el punto correspondiente a $(3,1)$ hacia el correspondiente a $(0,2)$, la dirección es $\ldots$ pulsa en 'Ver' cuando la tengas.
Ver
Restando las componentes del segundo punto de las del primero y dividiendo por el módulo, tendremos
$${\bf w}=\frac{1}{\sqrt{10}}(-3,1)$$
Paso 2
Ahora debemos hallar la derivada direccional de $f$ respecto de ${\bf w}$ en $(3,1)$. Puesto que $f$ es diferenciable en $(3,1)$, $$D_{\bf w}f=\nabla f\cdot {\bf w}$$ o bien, $$D_{\bf w}f=\frac{2-\sqrt{5}}{3}\frac{-3}{\sqrt{10}}-\frac{4+\sqrt{5}}{3}\frac{1}{\sqrt{10}}=\frac{-10+2\sqrt{5}}{3\sqrt{10}}$$Paso 3
Una vez conocida la pendiente de la trayectoria, debemos calcular su arcotangente, que nos dará el ángulo, $\alpha$, que forma con la horizontal. La variación en la altura de la bola es $$3\,\mbox{sen}\, \alpha$$ Para hacer estos cálculos recurrimos a una calculadora o al ordenador. Inténtalo y pulsa en 'Ver' cuando lo tengas.
Ver
escribiendo
w=[-3/sqrt(10),1/sqrt(10)]; % dirección en el plano m=sum([(2-sqrt(5))/3 -(4+sqrt(5))/3].*w); % derivada dirección según w 3*sin(atan(m)) % incremento verticalconcluimos que el incremento vertical es -1.5104.
Una alternativa para el cálculo del cambio de altura es utilizar el vector tangente a la trayectoria
$${\bf U}=\frac{1}{\sqrt{10}}\left(-3,1,\frac{-10+2\sqrt{5}}{3}\right)$$
y normalizarlo a $1$;
la tercera componente de $3\frac{{\bf U}}{|{\bf U}|}$ es la variación pedida. Lo podemos calcular en el ordenador con las siguientes líneas
Para ello añadimos las siguientes a las líneas anteriores:
w=[-3/sqrt(10),1/sqrt(10)]; % dirección en el plano m=sum([(2-sqrt(5))/3 -(4+sqrt(5))/3].*w); % derivada dirección según w v=[w m]; % vector tangente a la trayectoria pf=[3 1 2]+3*v/norm(v); % coordenadas del punto final del recorrido pf(3)-2 % variación de la altura de la bola desde el pto inicial hasta el finalPor último dibujamos la trayectoria (en azul) seguida por la bola sobre el plano tangente; en verde se dibuja la dirección en el plano $z=0$.

Para ello añadimos las siguientes a las líneas anteriores:
plot3(3, 1 ,2,'*') % dibujo del punto hold on quiver(3,1,w(1), w(2)) % dirección en el plano z=0 plot3([3 pf(1)],[1 pf(2)],[2 pf(3)]) % trayectoria de la bola [X,Y]=meshgrid(.5:3.5,0:2); % malla para dibujar el plano surf(X,Y,2+(2-sqrt(5))*(X-3)/3-(4+sqrt(5))*(Y-1)/3) % porción del plano tangente shading interp alpha(.6) view([206,46]) grid on hold off