Índice de tema

 

Enunciado

Determina el desarrollo de $f(x)=(x^2+1)e^{-x}$ en serie de potencias centrado en $a=2$, indicando el campo de convergencia de la serie resultante,
  1. utilizando el desarrollo de $e^{-x}$;
  2. mediante el cálculo de la derivada $n$-ésima por la fórmula de Leibniz.
Una vez obtenido el desarrollo compara su suma parcial correspondiente a $n=4$ con el polinomio de Taylor grado 4 que se obtiene en el ordenador (comando 'taylor' del paquete simbólico)

Resolución con el primer método

Escribiremos los desarrollos de $x^2+1$ y de $e^{-x}$ y haremos su producto. Esto es factible porque el desarrollo de $x^2+1$ es finito.

Paso 1

Encontrar el desarrollo de $x^2+1$ en potencias de $x-2$: podemos hacerlo de muchas maneras, por ejemplo, utilizando el desarrollo de Taylor o dividiendo entre $x-2$ o simplemente escribiendo $$x^2+1=a_2(x-2)^2+a_1(x-2)+a_0$$ y calculando los coeficientes $a_0$, $a_1$ y $a_2$ para que esta última igualdad sea cierta. Hazlo y pulsa en 'Ver'.
Ver
De $$x^2+1=a_2x^2+(-4a_2+a_1)x+a_0-2a_1+4a_2$$ tendremos que $$a_2=1 \ \ ,\ \ -4a_2+a_1=0\ \ ,\ \ a_0-2a_1+4a_2=1$$ de donde $$a_2=1 \ \ ,\ \ a_1=4\ \ ,\ \ a_0=5$$ Así que el desarrollo de potencias de $x^2+1$ centrado en $a=2$ es $$x^2+1=5+4(x-2)+(x-2)^2$$

Paso 2

Encontrar el desarrollo de $e^{-x}$ en potencias de $x-2$. Podemos
utilizar la fórmula de Taylor
utilizar el desarrollo de $e^{-x}$ en potencias de $x$
cualquiera de las otras dos opciones
esta es una buena opción, pero también lo es la otra. Elige la opción de las dos para poder ver cómo se hace de las dos formas.
esta es una buena opción, pero también lo es la otra. Elige la opción de las dos para poder ver cómo se hace de las dos formas.
En efecto podemos hacerlo de las dos maneras:
  • Para hacer el desarrollo de Taylor, debemos encontrar la derivada $n$-ésima de $g(x)=e^{-x}$ y evaluarla en $a=2$: $$g(x)=e^{-x}\ \ \Rightarrow \ \ g^{(n}(x)=(-1)^ne^{-x}\ \ \Rightarrow \ \ g^{(n}(2)=(-1)^ne^{-2}$$ Por tanto $$g(x)=e^{-x}=\sum_{n=0}^\infty \frac{(-1)^n e^{-2}}{n!}(x-2)^n=e^{-2}\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^n \ \ \ ,\ \ \ x\in{\bf R}$$
  • Si quisiéramos hacerlo utilizando el desarrollo de $g(x)=e^{-x}$ en potencias de $x$, que es $$g(x)=e^{-x}=\sum_{n=0}^\infty \frac{(-1)^n}{n!}x^n \ \ \ ,\ \ \ x\in{\bf R}$$ tendríamos que hacer el desarrollo de $g(x-2)$: $$h(x)=g(x-2)=e^{-(x-2)}=\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^n \ \ \ ,\ \ \ x\in{\bf R}$$ pero puesto que $$e^{-(x-2)}=e^{2}e^{-x}\ \ \Rightarrow \ \ g(x)=e^{-x}=e^{-2}h(x)$$ deducimos que $$g(x)=e^{-x}=e^{-2}\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^n \ \ \ ,\ \ \ x\in{\bf R}$$

Paso 3

Ahora debemos multiplicar los desarrollos de $x^2+1$ y de $e^{-x}$: $$(x^2+1)e^{-x}=[5+4(x-2)+(x-2)^2]e^{-2}\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^n=$$ $$=e^{-2}\left[ 5\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^n+4\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^{n+1}+\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^{n+2}\right]$$ y escribir esta expresión como una única suma:
$$(x^2+1)e^{-x}= e^{-2}\sum_{n=0}^\infty (5+4+1) \frac{(-1)^n}{n!}(x-2)^n$$
La otra opción no es correcta.
No es correcto. No podemos reunir así los tres sumatorios en uno solo, pues no empiezan en la misma potencia de $x$.
En efecto, no podemos reunir así los tres sumatorios en uno solo, pues no empiezan en la misma potencia de $x$. Debemos sacar de los sumatorios los términos que no tengan grados comunes a los tres y escribirlos todos comenzando en $n=2$. Inténtalo y pulsa en 'Continuar'.
  • el primero: $$\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^n=1-(x-2)+\sum_{n=2}^\infty \frac{(-1)^n}{n!}(x-2)^n$$
  • el segundo: $$\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^{n+1}=(x-2)+\sum_{n=1}^\infty \frac{(-1)^n}{n!}(x-2)^{n+1}=(x-2)+\sum_{n=2}^\infty \frac{(-1)^{n-1}}{(n-1)!}(x-2)^{n}$$
  • y el tercero: $$\sum_{n=0}^\infty \frac{(-1)^n}{n!}(x-2)^{n+2}=\sum_{n=2}^\infty \frac{(-1)^n}{(n-2)!}(x-2)^{n}$$
Ahora los combinamos, $$(x^2+1)e^{-x}=e^{-2}\left[ 5+(-5+4)(x-2) +5 \sum_{n=2}^\infty \frac{(-1)^n}{n!}(x-2)^n+4\sum_{n=2}^\infty \frac{(-1)^{n-1}}{(n-1)!}(x-2)^{n}+\sum_{n=2}^\infty \frac{(-1)^n}{(n-2)!}(x-2)^{n}\right]=$$ $$=e^{-2}\left[ 5-(x-2)+ \sum_{n=2}^\infty (-1)^n \left(\frac{5}{n!}-\frac{4}{(n-1)!}+\frac{1}{(n-2)!}\right)(x-2)^n\right]=$$ $$= e^{-2}\left[5-(x-2)+ \sum_{n=2}^\infty (-1)^n \frac{n^2-5n+5}{n!}(x-2)^n\right]$$ Observamos que esta serie puede escribirse englobando todos los términos en el sumatorio: $$(x^2+1)e^{-x}=e^{-2} \sum_{n=0}^\infty (-1)^n \frac{n^2-5n+5}{n!}(x-2)^n \ \ \ ,\ \ \ x\in{\bf R}$$

Resumen primer método

  1. encontrar el desarrollo de $x^2+1$ en potencias de $x-2$,
  2. encontrar el desarrollo de $e^{-x}$ en potencias de $x-2$,
  3. multiplicar esos desarrollos, lo que implica sacar algunos términos de los sumatorios y mover el índice.

Resolución utilizando la fórmula de Leibniz

Se trata aquí de encontrar el mismo desarrollo del apartado anterior pero utilizando la fórmula de Taylor y recurriendo a la fórmula de Leibniz para la derivada de un producto para hallar la derivada $n$-ésima de la función.

Paso 1

Encontrar la derivada $n$-ésima de $f(x)=(x^2+1)e^{-x}$. Inténtalo con la fórmula de Leibniz; ten en cuenta que las derivadas de $x^2+1$ son nulas a partir de la tercera incluida, lo que significa que el sumatorio tendrá sólo tres términos: para $k=0$, $k=1$ y $k=2$. Pulsa en 'Ver' después.
Ver
Aplicando la fórmula de Leibniz; $$\frac{d^n}{dx^n} (x^2+1)= \left(\begin{array}{c}n \\ 0\end{array}\right)(x^2+1)\frac{d^n}{dx^n} (e^{-x})+ \left(\begin{array}{c}n \\ 1\end{array}\right)2x\frac{d^{n-1}}{dx^{n-1}} (e^{-x})+ \left(\begin{array}{c}n \\ 2\end{array}\right)2\frac{d^{n-2}}{dx^{n-2}} (e^{-x})$$ Los coeficientes son $$\left(\begin{array}{c}n \\ 0\end{array}\right)=1 \ \ ,\ \ \left(\begin{array}{c}n \\ 1\end{array}\right)=n\ \ ,\ \ \left(\begin{array}{c}n \\ 2\end{array}\right)=\frac{n!}{2(n-2)!}=\frac{1}{2}n(n-1)$$ y la derivada de orden $k$ de $e^{-x}$ es $(-1)^k e^{-x}$. Por tanto $$f^{(n} (x)=\frac{d^n}{dx^n} (x^2+1)=(-1)^n(x^2+1)e^{-x}+2nx(-1)^{n-1}e^{-x}+n(n-1)(-1)^ne^{-x}=$$ $$=(-1)^ne^{-x}[x^2+1-2nx+n(n-1)]$$

Paso 2

Escribir la serie de Taylor de $f$ centrada en $a=2$: elige la correcta
$$f(x)=(x^2+1)e^{-x}=\sum_{n=0}^\infty \frac{f^{(n} (x)}{n!}(x-2)^n$$
$$f(x)=(x^2+1)e^{-x}=\sum_{n=0}^\infty \frac{f^{(n} (2)}{n!}x^n$$
$$f(x)=(x^2+1)e^{-x}=\sum_{n=1}^\infty \frac{f^{(n} (2)}{n!}(x-2)^n$$
$$f(x)=(x^2+1)e^{-x}=\sum_{n=0}^\infty \frac{f^{(n} (2)}{n!}(x-2)^n$$
Esa no es la correcta. Las derivadas deben ir evaluadas en $a=2$. ¡No podemos meter ahí funciones! La variable va únicamente en el término $(x-2)^n$ que para eso es una serie de potencias.
Esa no es la correcta. La serie debería estar centrada en $a=2$; la que has elegido no lo está.
¿Por qué desde $n=1$?
En efecto, esa es la correcta. Evaluamos $f^{(n} (2)$ y sustituimos. Termina tú y pulsa en 'Continuar'
$$f^{(n} (2)=(-1)^n e^{-2}(5-5n+n^2) \ \ \Rightarrow \ \ (x^2+1)e^{-x}=e^{-2}\sum_{n=0}^\infty \frac{(-1)^n (5-5n+n^2)}{n!}(x-2)^n$$

Paso 3

Encontramos el campo de convergencia de esta serie aplicando el criterio del cociente a la serie de términos absolutos:
La otra opción no es correcta.
$$\lim_{n\rightarrow \infty} \left|\frac{5-5(n+1)+(n+1)^2}{(n+1)!}\frac{n!}{5-5n+n^2}\right||x-2|=$$ $$=\lim_{n\rightarrow \infty}\frac{1-3n+n^2}{5-5n+n^2}\frac{1}{n+1}|x-2|=0\ \ ,\ \ \forall x$$ radio de convergencia $\infty$
¿Cuál piensas que es el error? No hay error, la propuesta es correcta.
En efecto, la serie converge en todos los reales. Así que $$(x^2+1)e^{-x}=e^{-2} \sum_{n=0}^\infty (-1)^n \frac{n^2-5n+5}{n!}(x-2)^n \ \ \ ,\ \ \ x\in{\bf R}$$

Paso 4

Aunque el enunciado no lo indique, podemos trazar las gráficas de unas cuantas sumas parciales junto con la función suma $$S_1(x)=e^{-2}\sum_{n=0}^1(-1)^n \frac{n^2-5n+5}{n!}(x-2)^n\ \ ,\ \ S_2(x)=e^{-2}\sum_{n=0}^2(-1)^n \frac{n^2-5n+5}{n!}(x-2)^n $$ $$ S_3(x)=e^{-2}\sum_{n=0}^3(-1)^n \frac{n^2-5n+5}{n!}(x-2)^n \ \ ,\ \ S_4(x)=e^{-2}\sum_{n=0}^4(-1)^n \frac{n^2-5n+5}{n!}(x-2)^n$$ $$S_5(x)=e^{-2}\sum_{n=0}^5(-1)^n \frac{n^2-5n+5}{n!}(x-2)^n \ \ ,\ \ S(x)=(x^2+1)e^{-x}$$ en el intervalo $(0,4)$. Podemos tomar cualquier intervalo, pues el desarrollo es válido en todos los reales. Aquí se ha elegido un intervalo centrado en $a=2$, que es el punto de contacto de todas las gráficas. Escribe las líneas con las que dibujas esas seis gráficas y pruébalas en el ordenador. Pulsa después en 'Ver'.
Ver
Una opción es escribir, 
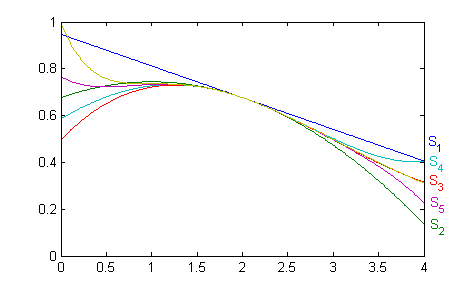
f=@(x,n) exp(-2)*(-1)^n*(5-5*n+n^2)*(x-2).^n/(factorial(n));
x=0:.01:4;
s(1,:)=f(x,1)+5*exp(-2);
for k=2:5
s(k,:)=s(k-1,:)+f(x,k);
end
s(6,:)=(x.^2+1).*exp(-x);
plot(x,s)
clear
Con estas líneas obtenemos la siguiente figura, donde la gráfica amarilla es la de la función $S(x)$.
Gráfica

Resumen

  1. hallar la derivada $n$-ésima de la función que se va a desarrollar en serie,
  2. hacer la serie de Taylor de centro $a=2$,
  3. estudiar campo de convergencia de la serie obtenida,
  4. dibujar unas sumas parciales y la función suma.
Hemos de comparar la suma parcial $$S_4(x)=e^{-2}\sum_{n=0}^4(-1)^n \frac{n^2-5n+5}{n!}(x-2)^n$$ que es el polinomio de Taylor de $f(x)=(x^2+1)e^{-x}$ de grado 4 y centro $a=2$, con el que se obtiene en el ordenador. Para calcular cómodamente los coeficientes de $S_4(x)$ es escribimos 
n=0:4;    %se define un vector de índices
sym((-1).^n.*(n.^2-5*n+5)./factorial(n)) % se calculan los coeficientes (salvo el e^{-2})
donde se ha utilizado el comando 'sym' para que presente los números en forma de fracción. Ahora pedimos el polinomio de Taylor de grado 4 y centro $a=2$ con 
syms x  % se declara x como simbólica
pretty(taylor((x^2+1)*exp(-x),5,2)) % se calcula el polinomio de Taylor de grado 4 en a=2
Puedes comprobar que efectivamente los coeficientes son iguales.