Suma y aplicación de una serie de potencias

Enunciado

Dada la serie de potencias $$S(x)=\sum_{n=1}^\infty \frac{x^{4n-3}}{4n-3}$$

Determina su campo de convergencia
Encuentra la expresión de la suma $S(x)$ para los valores de $x$ del campo de convergencia, utilizando derivación.
Como caso particular, calcula el valor de la suma numérica siguiente $$\sum_{n=1}^\infty \frac{1}{(4n-3)2^{4n-3}}$$
Dibuja en el ordenador las primeras cuatro sumas parciales de la serie de potencias en el intervalo $(-.9,.9)$, así como la función suma $S(x)$.

Resolución del primer apartado

Sabemos que el intervalo de convergencia de una serie de potencias como ésta es siempre un intervalo centrado en el punto $x=0$.

Paso 1

Hemos de empezar encontrando el radio de convergencia de esta serie. Estudiando la convergencia absoluta de la serie mediante el criterio del cociente $\ldots$ hazlo tú y pulsa en 'Ver' cuando lo tengas.

Ver

En efecto, haciendo $$\lim_{n\rightarrow \infty} \left| \frac{x^{4n+1}}{4n+1}\frac{4n-3}{x^{4n-3}}\right| =\lim_{n\rightarrow \infty}\frac{4n-3}{4n-1}x^4=x^4$$ sabemos que el intervalo de convergencia contendrá aquellos valores $x$ para los cuales $x^4<1$, es decir, $-1< x<1$. El radio de convergencia es $R=1$.

Sabiendo que el radio es 1, podemos concluir que

El campo de convergencia es el intervalo $(-1,1)$

La serie converge al menos en el intervalo $(-1,1)$

No es correcto, la serie podría ser también covergente en $x=-1$ y $x=1$. El campo de convergencia puede ser mayor que el intervalo de convergencia.

En efecto, para hallar el campo de convergencia conocido el intervalo, hay que estudiar la convergencia en los extremos, en este caso $x=-1$ y $x=1$.

Paso 2

Veamos qué ocurre en $x=-1$: en la expresión de la serie de potencias, sustituye $x$ por $-1$ y analiza la serie numérica resultante; pulsa en 'Ver' cuando lo tengas.

Ver

$$S(-1)=\sum_{n=1}^\infty \frac{(-1)^{4n-3}}{4n-3}=-\sum_{n=1}^\infty \frac{1}{4n-3}$$ es una serie que podemos comparar con la armónica, concluyendo que es divergente.

Paso 3

De manera anóloga estudiamos la convergencia en $x=1$: pulsa en 'Ver' cuando lo tengas.

Ver

$$S(1)=\sum_{n=1}^\infty \frac{1}{4n-3}$$ es una serie divergente. Ahora sí podemos concluir que el campo de convergencia de esta serie de potencias es $(-1,1)$.

Resolución del segundo apartado

Para realizar la suma de esta serie haremos previamente la suma de la serie de sus derivadas y después integraremos la función resultante:

Paso 1

Derivar la serie: puesto que se trata de una serie de potencias, podemos aplicar que la derivada de la suma $S(x)$ es la suma de la serie de las derivadas de cada término. Encuentra la serie de las derivadas y pulsa en 'Ver'.

Ver

$$S'(x)=\frac{d}{dx}S(x)=\sum_{n=1}^\infty \frac{4n-3}{4n-3}\, x^{4n-4}=\sum_{n=1}^\infty x^{4(n-1)}= \sum_{n=0}^\infty x^{4n}$$ donde la última expresión se ha obtenido desplazando el índice en una unidad.

Paso 2

Utilizando la suma de la serie geométrica , llegamos a que la suma de la serie $S'(x)$ es

$$\left(\frac{1}{1-x}\right)^4 $$

$$\frac{1}{1+x}$$

$$\frac{1}{1+x^4}$$

$$\frac{1}{1-x^4}$$

Descabellado. Eso se podría hacer si una suma elevada a la cuatro fuera igual a la suma de los sumandos elevados a la cuatro.

$S'(x)$ sí es una serie geométrica, pero la razón no es $-x$

$S'(x)$ sí es una serie geométrica de razón $x^4$, pero está mal la suma

Correcto, $S'(x)$ es una serie geométrica de razón $x^4$, luego ésa es su suma.

Paso 3

Una vez sumada $S'(x)$, encontramos $S(x)$ mediante integración: $$S(x)=\int S'(x)\, dx=\int \frac{dx}{1-x^4}$$ Intenta hacer esta primitiva; puedes ver después el proceso. El resultado es $$S(x)=\int \frac{dx}{1-x^4}=\frac{1}{2}\mbox{arctg}\, x+\frac{1}{4} \log\frac{1+x}{1-x}+C$$ donde queda por determinar el valor de la constante $C$. Para ello debemos conocer el valor de $S(x)$ en algún punto; obviamente ese valor es $S(0)=0$: $$S(0)=\frac{1}{2}\mbox{arctg}\, 0+\frac{1}{4} \log 1+C=0 \ \ \Rightarrow \ \ C=0$$ así que se concluye que $$S(x)=\frac{1}{2}\mbox{arctg}\, x+\frac{1}{4} \log\frac{1+x}{1-x}\ \ ,\ \ x\in (-1,1)$$

Resolución del tercer apartado

La serie numérica $$S=\sum_{n=1}^\infty \frac{1}{(4n-3)2^{4n-3}}$$ que ha de sumarse, es $S\left(\frac{1}{2}\right)$, por tanto $$S=S\left(\frac{1}{2}\right)=\frac{1}{2}\mbox{arctg}\,\frac{1}{2}+\frac{1}{4} \log 3$$

Resolución del cuarto apartado

Hemos de dibujar en $(-.9,.9)$ la gráfica de las funciones $$S_1(x)=\sum_{n=1}^1\frac{x^{4n-3}}{4n-3}=x\ \ ,\ \ S_2(x)=\sum_{n=1}^2 \frac{x^{4n-3}}{4n-3} \ \ ,\ \ S_3(x)=\sum_{n=1}^3\frac{x^{4n-3}}{4n-3} $$ $$S_4(x)=\sum_{n=1}^4 \frac{x^{4n-3}}{4n-3} \ \ ,\ \ S(x)=\frac{1}{2}\mbox{arctg}\, x+\frac{1}{4} \log\frac{1+x}{1-x}$$ Hay muchas maneras de generar esas gráficas, la que se presenta aquí es sólo una opción.

Por comodidad, definir el término general como una función de x y n:
```
f=@(x,n) x.^(4*n-3)/(4*n-3);
```
Generar el vector de abscisas sobre los que se trazarán las gráficas:
```
x=-.9:.1:.9;
```
Guardar en la primera fila de una matriz, s, los valores que toma la primera suma parcial:
```
s(1,:)=f(x,1);
```
En la fila k de la matriz s, se guardan los valores que toma la suma parcial k-ésima $S_k(x)$; eso lo hacemos con un ciclo for:
```
for k=2:4
	s(k,:)=s(k-1,:)+f(x,k);
end
```
La última fila de la matriz s serán los valores que toma la función $S(x)$:
```
s(5,:)=.5*atan(x)+.25*log((1+x)./(1-x));
```
Finalmente se traza la gráfica de cada fila de s respecto de las abscisas x:
```
plot(x,s)
```
Limpiamos, por si queremos repetir el proceso con otra dimensión para x:
```
clear
```

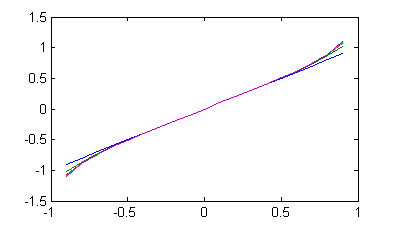
En la figura resultante la primera gráfica es la de color azul y la última la de color violeta:

f=@(x,n) x.^(4*n-3)/(4*n-3);
x=-.9:.1:.9;
s(1,:)=f(x,1);
for k=2:4
	s(k,:)=s(k-1,:)+f(x,k);
end
s(5,:)=.5*atan(x)+.25*log((1+x)./(1-x));
plot(x,s)

Resumen

Primer apartado: encontrar campo de convergencia
1. encontrar el intervalo de convergencia,
2. estudiar la convergencia en los extremos.
Segundo apartado: sumar la serie
1. derivar la serie término a término,
2. sumar la serie de las derivadas,
3. integrar el resultado anterior.
Tercer apartado: aplicación a una serie numérica
1. reconocer la serie a sumar como la serie de potencias evaluada en cierto $x$,
2. evaluar la función suma en ese valor $x$.

Índice de tema