Enunciado
Se considera la función $f(x)=\mbox{sen}\, x$ en el intervalo $[0,\frac{\pi}{4}]$.
- Extiende la función $f(x)$ como función $\frac{\pi}{2}$-periódica que presente simetría par, mediante un desarrollo de Fourier de cosenos.
- Extiende la función $f(x)$ como función $\frac{\pi}{2}$-periódica que presente simetría impar, mediante un desarrollo de Fourier de senos.
- Escribe el desarrollo anterior en forma armónica.
- Escribe el código Matlab de una función que represente el espectro de amplitudes de la serie anterior para $m+1$ múltiplos de la frecuencia fundamental, siendo $m$ la variable de entrada de la función.
Resolución del primer apartado
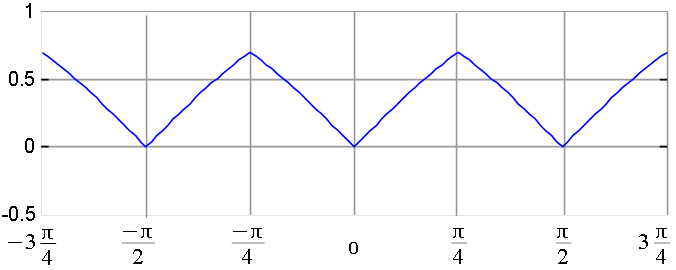
Dibujamos una muestra de la extensión $\frac{\pi}{2}$-periódica par, por ejemplo en un intervalo que abarca tres periodos:
Incorrecto
Correcto
No; míralo bien.
En efecto, esas expresiones son correctas. La función $f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos 4nx$ es la extensión simétrica par en un periodo y $\frac{\pi}{2}$-periódica. Calcumos las integrales que conducen a $a_n$. Para hallar las correspondientes a $n\neq 0$ debes utilizar que
$$\mbox{sen}\, a\, \cos b=\frac{1}{2}[\mbox{sen}\,(a+b)+\mbox{sen}\,(a-b)]$$ Encuentra los coeficientes $a_n$ y pulsa después en 'Continuar'.
$$a_0=\frac{8}{\pi}\int_0^{\pi/4} \mbox{sen}\, x \, dx=\left[-\frac{8}{\pi}\cos x\right]_0^{\pi/4}=\frac{4}{\pi}(2-\sqrt{2})$$
$$a_n=\frac{8}{\pi}\int_{0}^{\pi/4} \mbox{sen}\, x\, \cos 4nx\, dx=\frac{4}{\pi}\int_{0}^{\pi/4}[\mbox{sen}(4n+1)x-\mbox{sen}(4n-1)x]\, dx=$$
$$=\frac{4}{\pi}\left[\frac{-\cos (4n+1)x}{4n+1}+\frac{\cos (4n-1)x}{4n-1}\right]_0^{\pi/4}=$$
$$=\frac{4}{\pi}\left[\frac{-1}{4n+1}\cos \left(n\pi+\frac{\pi}{4}\right)+\frac{1}{4n-1}\cos \left(n\pi-\frac{\pi}{4}\right)+\frac{1}{4n+1}-\frac{1}{4n-1}\right]=$$$$=\frac{4}{\pi}\left[\frac{-1}{4n+1}(-1)^n\frac{\sqrt{2}}{2}+\frac{1}{4n-1}(-1)^n\frac{\sqrt{2}}{2}+\frac{1}{4n+1}-\frac{1}{4n-1}\right]=$$
$$=\frac{4}{\pi}\left(\frac{-1}{4n+1}+\frac{1}{4n-1}\right)\left[(-1)^n\frac{\sqrt{2}}{2}-1\right]=\frac{4}{\pi(16n^2-1)}[\sqrt{2}(-1)^n-2]$$
con lo cual la serie buscada es
$$f(x)=\frac{4}{\pi}\left[1-\frac{\sqrt{2}}{2}+\sum_{n=1}^\infty \frac{\sqrt{2}(-1)^n-2}{16n^2-1} \cos 4nx\right]$$
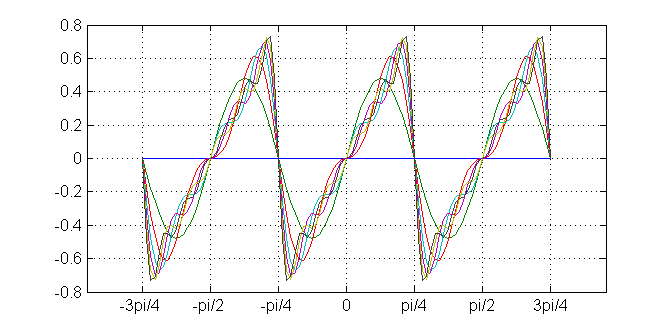
La siguiente figura muestra las gráficas de las siete primeras sumas parciales de esta serie:
Resolución del segundo apartado
Dibujamos una muestra de la extensión $\frac{\pi}{2}$-periódica impar en un periodo, por ejemplo en un intervalo que abarca tres periodos: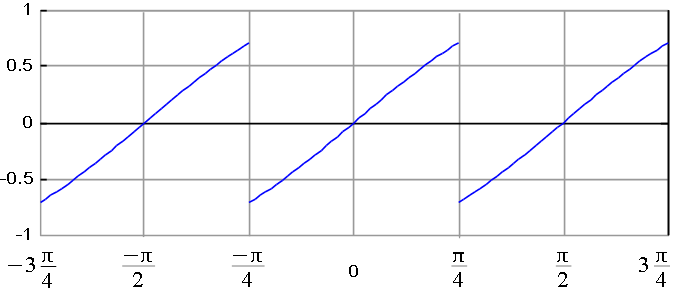
Incorrecto
Correcto
No; míralo bien.
En efecto, esas expresiones son correctas. La función $f(x)=\sum_{n=1}^\infty b_n\mbox{sen}\, 4nx$ es la extensión simétrica impar en un periodo y $\frac{\pi}{2}$-periódica. Calcumos las integrales que conducen a $b_n$. Para hallarlas puedes utilizar que
$$\mbox{sen}\, a\, \mbox{sen}\, b=\frac{1}{2}[\cos(a-b)-\cos\,(a+b)]$$ Encuentra los coeficientes $b_n$ y pulsa después en 'Continuar'.
$$b_n=\frac{8}{\pi}\int_{0}^{\pi/4} \mbox{sen}\, x\,\mbox{sen}\, 4nx\, dx=\frac{4}{\pi}\int_{0}^{\pi/4}[\cos(4n-1)x-\cos(4n+1)x]\, dx=$$
$$=\frac{4}{\pi}\left[\frac{\mbox{sen} (4n-1)x}{4n-1}-\frac{\mbox{sen}(4n+1)x}{4n+1}\right]_0^{\pi/4}=$$
$$=\frac{4}{\pi}\left[\frac{1}{4n-1}\mbox{sen}\, \left(n\pi-\frac{\pi}{4}\right)-\frac{1}{4n+1}\mbox{sen}\, \left(n\pi-\frac{\pi}{4}\right)\right]=$$$$=\frac{4}{\pi}\left[\frac{1}{4n-1}(-1)^{n+1}\frac{\sqrt{2}}{2}-\frac{1}{4n+1}(-1)^{n}\frac{\sqrt{2}}{2}\right]=$$
$$=\frac{4}{\pi}(-1)^{n+1}\frac{\sqrt{2}}{2}\left[\frac{1}{4n-1}+\frac{1}{4n+1}\right]=\frac{16\sqrt{2}}{\pi}\frac{(-1)^{n+1}n}{(16n^2-1)}$$
con lo cual la serie buscada es
$$f(x)=\frac{16\sqrt{2}}{\pi}\sum_{n=1}^\infty \frac{(-1)^{n+1}n}{(16n^2-1)} \mbox{sen}\, 4nx$$
La siguiente figura muestra las gráficas de las seis primeras sumas parciales de esta serie:
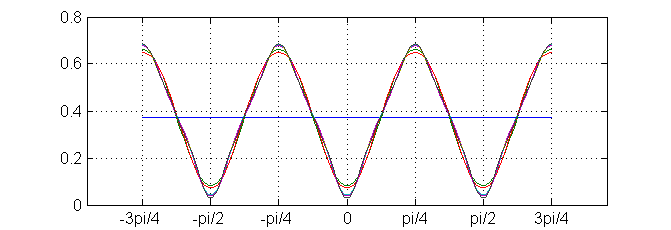
Resolución del tercer apartado
La serie de Fourier en forma armónica puede escribirse en términos de senos o de cosenos. Puesto que en el caso que nos ocupa la serie es sólo de senos, parece más apropiado escribir su forma armónica con armónicos tipo seno. Siguiendo las fórmulas genéricas, tendremos que $$A_n=|b_n|=\frac{16\sqrt{2}}{\pi}\frac{n}{(16n^2-1)}\ ,\ \phi_n=\mbox{arctg}\frac{a_n}{b_n}=0\ \ \Rightarrow\ \ f(x)=\frac{16\sqrt{2}}{\pi}\sum_{n=1}^\infty \frac{n}{(16n^2-1)} \mbox{sen}\, 4nx$$
Correcto
Incorrecto
No; algo debe de estar mal porque si no tendríamos la misma expresión que en la serie trigonométrica pero sin el factor $(-1)^{n+1}$.
En efecto, es incorrecto, algo debe de estar mal en esas expresiones porque si no tendríamos la misma expresión que en la serie trigonométrica pero sin el factor $(-1)^{n+1}$. El error está en la construcción de las fases $\phi_n=\mbox{arctg}\frac{a_n}{b_n}$. Es cierto que $a_n=0$, pero debes tener en cuenta el signo de $b_n$:
- el signo de $b_n$ para $n$ impar es positivo, luego $\phi_n=0$
- el signo de $b_n$ para $n$ par es negativo, luego $\phi_n=\pi$
$$f(x)=\frac{16\sqrt{2}}{\pi}\sum_{n=1}^\infty \frac{n}{(16n^2-1)} \mbox{sen}(4nx+(n+1)\pi)$$
Observa que esa es la expresión que obtendríamos de la serie trigonométrica si el signo de cada sumando la determinara el seno, de esta forma, cuando el coeficiente $b_n$ es negativo, hemos de sumar $\pi$ al argumento del seno (o lo que es lo mismo, un múltiplo impar de $\pi$), pero cuando el coeficiente $b_n$ es positivo, hemos de dejar el seno igual o lo que es lo mismo, sumarle un múltiplo par de $\pi$.
Resolución del cuarto apartado
Hemos de generar una función que dibuje el espectro de amplitudes, podemos seguir los siguientes pasos:- Declaración de la función, con su nombre y argumento de entrada
- definir un vector con las frecuencias sobre las que se considerarán las amplitudes
- guardar por separado la amplitud $A_0$
- definir el vector de amplitudes
- trazar la gráfica de los puntos con el comando plot
- para dar mayor claridad, pueden fijarse que las marcas del eje horizontal sean las frecuencias utilizadas
- también para mayor claridad puede añadirse una rejilla y poner etiquetas a los ejes
- cerrar la función
Ver
Podríamos escribir
function espectroamplitudes(m)
w=4; n=1:m; % frecuencia fundamental y vector con naturales
mw=w*n; % vector con multiplos de la frecuencia fundamental
A0=2*(2-sqrt(2))/pi; % amplitud inicial
A=16*sqrt(2)*n./(pi*(16*n.^2-1)); % vector de amplitudes
plot([0 mw],[A0 A], 'o') % dibujo de los puntos
set(gca,'XTick',[0 mw]) % fijamos que las marcas del eje horizontal sean las frecuencias tomadas
grid on
xlabel('frecuencias nw');ylabel('amplitudes') % etiquetas para los ejes
end
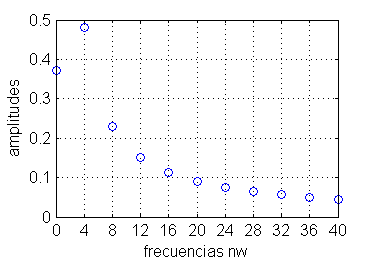
Si ahora en la ventana de comandos ejecutamos por ejemplo
espectroamplitudes(10)se obtiene la siguiente figura