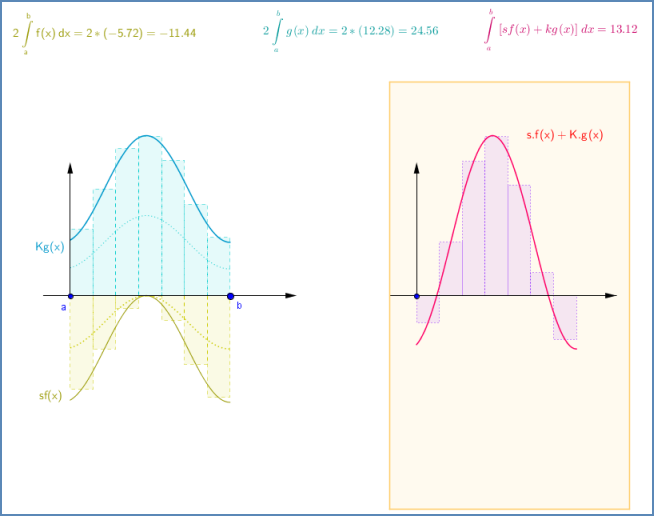
PROPIEDAD 1 (Carácter lineal de la integral definida).- Si $f(x)$ y $g(x)$ son dos funciones integrables en $\left[ {a,b} \right]$ también son integrables las funciones $f(x) \pm g(x)$ y $kf(x)$ con $k \in R$, cumpliéndose:
(i) $\int\limits_a^b {(f(x) \pm g(x))dx = \int\limits_a^b {f(x)dx} } \pm \int\limits_a^b {g(x)dx} $
(ii) $\int\limits_a^b {kf(x)dx = k\int\limits_a^b {f(x)dx} } $

 

Laboratorio: Combinación lineal de funciones

 

 

PROPIEDAD 2 (Inversión de los límites de integración).- Si se invierten los límites de una integral ésta cambia de signo, $$\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} $$

 

PROPIEDAD 3.- Para todo número real $a$ se tiene $\int\limits_a^a {f(x)dx} = 0$

 

PROPIEDAD 4 (Propiedad aditiva del intervalo de integración).- Si $f(x)$ es integrable en los intervalos $\left[ {a,b} \right]$ y $\left[ {b,c} \right]$ con $a < b < c$ entonces $f$ es integrable en $\left[ {a,c} \right]$ siendo, $$\int\limits_a^c {f(x)dx} = \int\limits_a^b {f(x)dx} + \int\limits_b^c {f(x)dx} $$

 

PROPIEDAD 5 (Positividad).- Si $f$ es integrable y no negativa en $\left[ {a,b} \right]$, entonces $$\int\limits_a^b {f(x)dx} \ge 0$$

 

PROPIEDAD 6 (Propiedad de monotonía).- Si $f$ y $g$ son integrables en $\left[ {a,b} \right]$ y además $f(x) \le g(x)$, entonces $$\int\limits_a^b {f\left( x \right)dx} \le \int\limits_a^b {g\left( x \right)dx} $$

 

 

PROPIEDAD 7 (Acotación modular).- Se verifica $$\left| {\int\limits_a^b {f(x)dx} } \right| \le \int\limits_a^b {\left| {f(x)} \right|dx} $$

 

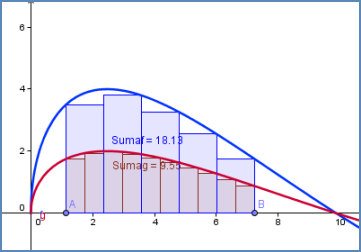
Ejercicios interactivos:

• Integrabilidad y propiedades