Enunciado
Consideramos de nuevo la lámina \(S\) dada por \(z=9-x^2-y^2\) en \(z>0\), cuya temperatura en cada punto es proporcional (\(k\)) al cuadrado de la distancia al origen de coordenadas. Teniendo en cuenta que el flujo de calor en cada punto es proporcional (\(c\)) al gradiente de la temperatura, calcula el flujo total de calor hacia fuera de \(S\) (puesto que aquí \(S\) no es una superficie cerrada, 'hacia fuera' significa desde la cara cóncava hacia la convexa). Puedes utilizar el teorema de la divergencia de Gauss para comprobar el resultado.
Paso 1
En primer lugar encontramos la expresión del campo vectorial flujo de calor. Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
$${\bf F}=c\nabla T =ck\nabla (x^2+y^2+z^2)=2ck(x,y,z)$$
Paso 2
Ahora, teniendo en cuenta cómo se realiza la integral de un campo vectorial sobre una superficie dada en cartesianas, necesitamos determinar el vector normal a la superficie en cada punto, correspondiente al sentido fijado en el enunciado. Éste será:
Ninguna de las opciones propuestas
$${\bf N}=2x+2y+1$$
$${\bf N}=(2x,2y,0)$$
$${\bf N}=(-2x,-2y,1)$$
$${\bf N}=(2x,2y,1)$$
Sí hay una propuesta correcta.
¡Eso no es un vector!
¿Por qué un cero en la tercera componente?
¡Cuidado con los signos! Fíjate bien.
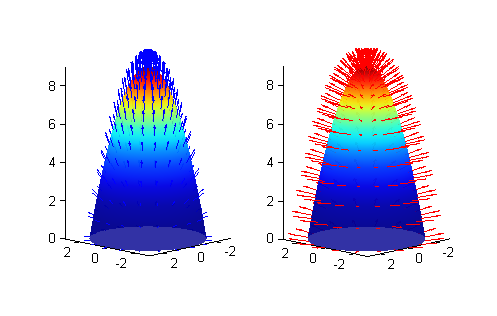
Ese es el vector normal en cada punto dado por \((-z'_x,-z'_y,1)\). En la figura puedes ver una muestra de los vectores del campo flujo de calor sobre la placa (izquierda) y una muestra de los vectores normales (derecha):
Paso 3
Multiplicamos escalarmente el campo flujo de calor por estos vectores normales y evaluamos el resultado en la superficie. Hazlo tú y pulsa en 'Ver'.
Ver
$${\bf F}\cdot{\bf N}=2ck(x,y,z)\cdot(2x,2y,1)=2ck(2x^2+2y^2+z)$$
Sobre la superficie \(z=9-x^2-y^2\),
$${\bf F}\cdot{\bf N}=2ck(x^2+y^2+9)$$
Paso 4
La región del plano proyección de la lámina ya está localizada en el ejercicio anterior. Así que planteamos ya la integral: $$\mbox{Flujo}=\int\!\!\int_{R_{xy}} 2ck (x^2+y^2+9)\, dA\ \ ,\ \ R_{xy}=\{(x,y)/x^2+y^2\leq 9\}$$ que se calculará pasando a polares. Termina el cálculo y pulsa en 'Ver'.
'Ver'
$$\mbox{Flujo}=2ck\int_0^{2\pi}\int_0^3 r(r^2+9)\, dr\, d\theta=4\pi ck\int_0^3 (r^3+9r)\, dr=$$
$$=4\pi ck \left[\frac{r^4}{4}+\frac{9}{2}r^2\right]_0^3=3^5\pi ck$$
Paso 5
Comprobamos ahora el resultado para el flujo utilizando el teorema de Gauss. La superfic¡e \(S\) no es cerrada, así que debemos 'cerrarla' uniéndola con el círculo de radio 3 y centro \((0,0)\) del plano XY. El flujo a través de esta superficie es
Igual al calculado para la superficie parabólica.
Nulo
No hay razón para ello.
Efectivamente es nulo porque el producto escalar del campo vectorial por el vector normal a ese disco (vector \({\bf k}\)), es nulo por ser \(z=0\). Por tanto, el flujo a través de la superficie \(S\) es la integral triple de la divergencia del campo en
$$H=\{(x,y,z) /\, (x,y)\in R_{xy},\, 0\leq z\leq 9-x^2-y^2\}$$
Halla esa integral y pulsa en 'Continuar' cuando la tengas.
$$\mbox{Flujo}= \int_0^{2\pi}\int_0^3\int_0^{9-r^2}6ck r \, dz\, dr\, d\theta=12 c k \pi \int_0^3(9r-r^3)\, dr= 3^5\pi ck$$
que es el mismo resultado obtenido haciendo la integral de flujo.
Resumen
- Encontrar el campo vectorial flujo de calor
- Hallar el vector normal a la superficie
- Encontrar la expresión del integrando: producto escalar del campo vectorial por la normal a la superficie
- Calcular la integral
- Aplicar el teorema de Gauss, teniendo en cuenta que debe cerrarse la superficie, para comprobar el resultado obtenido antes con la integral de flujo.