Índice de tema

 

Enunciado

El sólido $H$ ocupa la parte del primer octante limitada inferiormente por la superficie $z^2=x^2+y^2$ y superiormente por $x^2+y^2+z^2=8$.
  1. Utiliza coordenadas esféricas para calcular el volumen de $H$.
  2. Calcula el mismo volumen utilizando coordenadas cilíndricas.
  3. Dibuja en el ordenador las porciones de cono $z^2=x^2+y^2$ y de esfera $x^2+y^2+z^2=8$ que limitan $H$, utilizando coordenadas polares para el dominio.

Resolución del primer apartado

Paso 1

Escribir las ecuaciones de las superficies limitantes en coodenadas esféricas. Para hacer esto debemos conocer las ecuaciones que relacionan las coordenadas rectangulares cartesianas $(x,y,z)$ con las coordenadas esféricas $(\rho,\theta,\phi)$; si no te acuerdas puedes consultar la teoría sobre estas coordenadas.
  • Teniendo en cuenta que $$z^2=x^2+y^2\hspace{.6cm}\Rightarrow \hspace{.6cm} \rho^2\cos^2\phi=\rho^2\mbox{sen}^2\phi\,\cos^2\theta+\rho^2\mbox{sen}^2\phi\,\mbox{sen}^2\theta=\rho^2\mbox{sen}^2\phi$$ la ecuación en esféricas para la parte del cono $z^2=x^2+y^2$ en $z>0$ es
$\phi=\frac{\pi}{4}$ o $\phi=\frac{3\pi}{4}$
$\phi=\frac{\pi}{4}$ o $\phi=\frac{-\pi}{4}$
$\phi=\frac{\pi}{4}$
No es correcto; tienes que tener en cuenta que sólo debes tomar la parte del cono en $z\geq 0$, es decir, $\phi$ debe estar en $[0,\pi/2]$
No es correcto; la variable esférica $\phi$ se toma entre $0$ y $\pi$.
En efecto, $\phi=\frac{\pi}{4}$ en esféricas es equivalente a $z=\sqrt{x^2+y^2}$ en cartesianes rectangulares.
  • La esfera $x^2+y^2+z^2=8$ en esféricas es también una ecuación muy sencilla, no en vano está formada por todos los puntos que están a distancia $\sqrt{8}=2\sqrt{2}$ del origen: $$x^2+y^2+z^2=8\hspace{.6cm}\Rightarrow \hspace{.6cm} \rho=2\sqrt{2}$$

Paso 2

Escribimos ahora la región de integración utilizando estas coordenadas; el conjunto genérico $$S=\{(\rho,\theta,\phi)/\, \phi_1\leq \phi\leq\phi_2,\, \rho_1(\phi)\leq \rho\leq \rho_2(\phi),\, \theta_1(\phi,\rho) \leq \theta \leq \theta_2(\phi,\rho)\}$$ es en este caso $\ldots$ piénsalo y pulsa en 'Ver'.
Ver
$$S=\{(\rho,\theta,\phi)/\, 0\leq \phi\leq\frac{\pi}{4},\ 0\leq \rho\leq 2\sqrt{2},\ 0 \leq \theta \leq \frac{\pi}{2}\}$$ ya que
  • $\phi_1=0$, ya que el eje $0Z$ positivo, origen de la variable $\phi$, está en el sólido
  • $\phi_2=\frac{\pi}{4}$, ya que lo más 'lejos' que podemos 'bajar' desde el eje $0Z$ positivo, es el cono $\phi=\frac{\pi}{4}$
  • $\rho_1=0$, pues el origen está en el sólido
  • $\rho_2=2\sqrt{2}$, ya que la distancia mayor al origen es la esfera $\rho=2\sqrt{2}$
  • $\theta_1=0$, porque el semiplano $x>0$, origen de la variable $\theta$, está en el sólido
  • $\theta_2=\frac{\pi}{2}$, ya que éste es el semiplano $y>0$.
Observa que en esféricas, esta región es una caja pues los límites en las tres variables esféricas son constantes. Puedes dibujarla utilizando el ejecutable llamado 'Cajas cilíndricas y esféricas', que está en 
http://www.giematic.unican.es/DemosMatlab/IndiceMaterial.html

Paso 3

Plantear la integral triple. El volumen es el resultado de hacer la integral:
$$V=\int_0^{\pi/2}\int_0^{2\sqrt{2}}\int_0^{\pi/4} \ d\phi\ d\rho \ d\theta$$
$$V=\int_0^{\pi/2}\int_0^{2\sqrt{2}}\int_0^{\pi/4} \rho^2 \mbox{sen}\theta\ d\phi\ d\rho \ d\theta$$
$$V=\int_0^{\pi/2}\int_0^{2\sqrt{2}}\int_0^{\pi/4} \rho^2 \mbox{sen}^2\phi\ d\phi\ d\rho \ d\theta$$
$$V=\int_0^{\pi/2}\int_0^{2\sqrt{2}}\int_0^{\pi/4} \rho^2 \mbox{sen}\phi\ d\rho \ d\theta \ d\phi$$
Ninguna de las opciones propuestas es correcta.
Cuidado, falta el jacobiano. Fíjate que $d\phi\,d\rho \,d\theta$ tendría sólo dimensión 1 y no dimensión 3 como corresponde a un volumen.
El integrando no es correcto, repasa el jacobiano del cambio a esféricas.
El integrando no es correcto, repasa el jacobiano del cambio a esféricas.
El orden de los diferenciales no es el que corresponde a los extremos de integración.
En efecto, ninguna de las propuestas es correcta. La correcta es $$V=\int_0^{\pi/2}\int_0^{2\sqrt{2}}\int_0^{\pi/4} \rho^2 \mbox{sen}\phi\ d\phi\ d\rho \ d\theta$$ Calcúlala y pulsa en 'Continuar'.
Haciendo las tres integrales resulta $$V=\frac{\pi}{2}\frac{16}{3}\sqrt{2}\left(-\frac{\sqrt{2}}{2}+1\right)=\frac{8}{3}(\sqrt{2}-1)\pi$$

Resolución del segundo apartado

Paso 1

Puesto que una de las superficies limitantes es una esfera (simétrica respecto del eje $0Z$) y la otra un cono (simétrico respecto al eje $0Z$) es apropiado el uso de coordenadas cilíndricas. Debemos por tanto escribir en estas coordenadas las ecuaciones de la semiesfera y el semicono. Hazlo tú y pulsa en 'Ver'.
Ver
  • $$z^2=8-x^2-y^2\ , \ z>0 \hspace{.2cm} \Rightarrow \hspace{.2cm} z^2=8-r^2 \ , \ z>0 \hspace{.2cm} \Rightarrow \hspace{.2cm} z=\sqrt{8-r^2}$$
  • $$z^2=x^2+y^2\ , \ z>0 \hspace{.2cm} \Rightarrow \hspace{.2cm} z^2=r^2 \ , \ z>0 \hspace{.2cm} \Rightarrow \hspace{.2cm} z=r$$

Paso 2

Escribir los límites de la región de integración en coordenadas cilíndricas: $$S=\{(r,\theta,z)/\, \theta_1\leq \theta \leq \theta_2 ,\, r_1(\theta)\leq r\leq r_2(\theta),\, z_1(\theta,r)\leq z\leq z_2(\theta,r) \}$$ Estas variaciones son
$$0\leq \theta \leq \frac{\pi}{2},\ 0\leq r\leq 2\sqrt{2},\ r\leq z\leq \sqrt{8-r^2}$$
$$0\leq \theta \leq \frac{\pi}{2},\ 0\leq r\leq 2,\ 0\leq z\leq \sqrt{8-r^2}$$
$$0\leq \theta \leq \frac{\pi}{2},\ 0\leq r\leq 2,\ 0\leq z\leq r$$
$$0\leq \theta \leq \frac{\pi}{2},\ 0\leq r\leq 2,\ r\leq z\leq \sqrt{8-r^2}$$
No. El valor máximo que puede tomar $r$ es 2, pues la intersección entre $z=r$ y $z=\sqrt{8-r^2}$ es $r=2$.
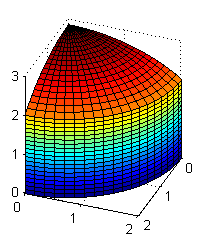
No. La coordenada $z$ debe ir desde su valor en el cono $z=r$ hasta su valor en la esfera $z=\sqrt{8-r^2}$. Si ponemos $0\leq z\leq \sqrt{8-r^2}$ estaríamos tomando el sólido limitado entre el plano $z=0$ y el casquete esférico, dentro del cilindro $r=2$:
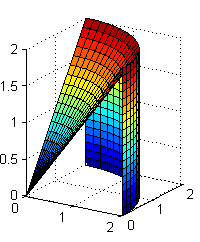
Gráfica
No. La coordenada $z$ debe ir desde su valor en el cono $z=r$ hasta su valor en la esfera $z=\sqrt{8-r^2}$. Si ponemos $0\leq z\leq r$ estaríamos tomando el sólido limitado entre el plano $z=0$ y el cono, dentro del cilindro $r=2$:
Gráfica
Esto es lo correcto. La coordenada $z$ va desde su valor en el cono $z=r$ hasta su valor en la esfera $z=\sqrt{8-r^2}$, para cada elección de $r$. Por tanto, la región es $$S=\{(r,\theta,z)/\, 0\leq \theta \leq \frac{\pi}{2},\ 0\leq r\leq 2,\ r\leq z\leq \sqrt{8-r^2} \}$$

Paso 3

Calcular la integral correspondiente a esta región y con la que se calcula el volumen. Plantéala y pulsa en 'Ver'.
Ver
El volumen es $$V=\int_0^{\pi/2}\int_0^2\int_r^{\sqrt{8-r^2}}\, r\ dz\ dr d\theta$$ haciendo las integrales resulta $$V=\frac{8}{3}(\sqrt{2}-1)\pi$$

Resolución del tercer apartado

Para dibujar las superficies limitantes del sólido correspondientes al cono y a la esfera hemos de tener en cuenta que se cortan en el arco de circunferencia $r=2$ correspondiente al primer cuadrante del plano $XY$ (en el plano $z=2$, aunque éste dato no se utiliza aquí). Para dibujarlas, hemos de construir una malla de puntos en el dominio $$\{(x,y)/ x^2+y^2\leq 4\}$$ utilizando coordenadas polares. Seguiremos por tanto los siguientes pasos, en cada uno pulsa en 'Continuar' cuando lo hayas hecho:
  • definir un vector r de 20 componentes con los valores del radio y otro, t, con los valores del ángulo 
r=linspace(0,2,20);
t=linspace(0,pi/2,20);
  • generar una malla con estos vectores r y t 
[R,T]=meshgrid(r,t);
  • definir las matrices X e Y a partir de la malla anterior 
X=R.*cos(T);
Y=R.*sin(T);
  • dibujar el cono y la esfera 
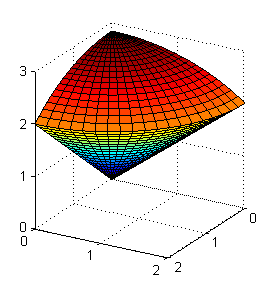
surf(X,Y,R)  % porción de cono
hold on
surf(X,Y,sqrt(8-R.^2)) % porción de esfera
hold off
Si además le añadimos 
view([120,20])
nos mostrará la figura siguiente
Gráfica