Coordenadas cilíndricas
Un punto $(x,y,z)$ del sistema cartesiano rectangular se escribe como $(r,\theta,z)$ en coordenadas cilíndricas si
- $r$: distancia del punto $(x,y,z)$ al eje $0Z$;
- $\theta$: ángulo en $[0,2\pi]$ que forma la proyección del radio vector de $(x,y,z)$ en el plano $XY$ con el semieje $0X$ positivo.
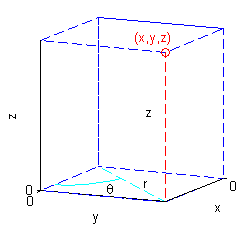
Por tanto, la relación entre las coordenadas cartesianas y las cilíndricas es
$$\left\{\begin{array}{lll} x=r\cos \theta \\
y=r\,\mbox{sen}\, \theta \\ z
\end{array}\right.$$
El jacobiano del cambio es
$$\frac{\partial(x,y,z)}{\partial(r,\theta,z)}=r$$
Las coordenadas cilíndricas están especialmente indicadas para expresar regiones del espacio que posean un eje de simetría, por ejemplo, sólidos limitados por cilindros o sólidos limitados por planos perpendiculares a un eje.
