Enunciado
Un sólido ocupa la región $H$ del espacio limitada por el cilindro parabólico de ecuación $z=1-y^2$ y por los planos $x+z=1$, $x=0$ y $z=0$. Halla la masa de este sólido sabiendo que en cada punto la densidad es $\rho(x,y,z)=z$.
Realizaremos el ejercicio siguiendo los siguientes pasos:
- Plantear la integral triple que conduce a la masa del sólido $H$.
- Hacer un bosquejo del sólido en los ejes coordenados.
- Encontrar los límites de integración en cada variable.
- Calcular las integrales iteradas.
Paso 1
¿Qué integral hay que hacer? Recordando las interpretaciones de la integral triple, vemos que hemos de hacer la integral triple de la función de densidad sobre el sólido. El integrando es conocido por el enunciado, así que sólo hay que ocuparse de la región de integración. Como ejercicio puede ser recomendable plantear y resolver esta integral en distintos órdenes de integración. Aquí hemos seleccionado tres: $$\mbox{Masa}=\int\!\!\int\!\!\int_H z\, dy\, dx\, dz$$ $$\mbox{Masa}=\int\!\!\int\!\!\int_H z\, dy\, dz\, dx$$ $$\mbox{Masa}=\int\!\!\int\!\!\int_H z\, dx\, dz\, dy$$ En las dos primeras se proyecta sobre el plano $XZ$ y en la tercera sobre el plano $YZ$.Paso 2
Aunque el enunciado no lo pide y no es imprescindible hacerlo, podemos incluir una representación gráfica del cilindro parabólico y del plano $x+z=1$, para que nos resulte más sencillo escribir después las integrales iteradas.- $z=1-y^2$ repite la misma curva (parábola) en todos los planos $x=$cte; esta curva, en el plano $YZ$ es una parábola de vértice $(0,1)$, que corta al eje $0Y$ en los puntos $(-1,0)$ y $(1,0)$
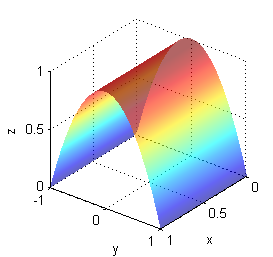
- el plano $x+z=1$ corta al plano $XZ$ en la recta $x+z=1$ y así se repite para todos los valores de $y$:
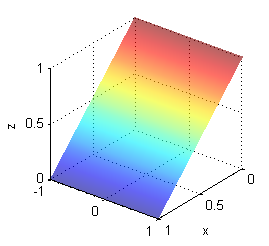
Ver
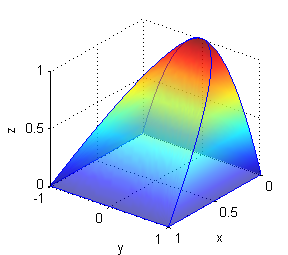
Paso 3 para el primer orden de integración
Proyectamos $H$ en el plano $XZ$ y luego sobre el eje $0Z$, es decir, escribimos el conjunto como $$H=\{(x,y,z) /\, z_1\leq z\leq z_2,\, x_1(z)\leq x\leq x_2(z),\, y_1(x,z)\leq y \leq y_2(x,z)\}$$ Los límites $z_1$ y $z_2$ son
$z_1=0$ y $z_2=1-x$
Ninguna de las dos propuestas es correcta
$z_1=0$ y $z_2=1$
¡No! $z_1$ y $z_2$ deben ser constantes. Son el menor y el mayor valor que puede tomar la variable $z$ en $H$.
Hay una correcta.
En efecto, $z_1$ es el menor valor que toma la variable $z$ en $H$ y $z_2$ el mayor.
Para cada valor de $z$ entre $z_1=0$ y $z_2=1$, la variable $x$ puede tomar valores entre $x_1(z)$ y
$x_2(z)$, que son
$x_1(z)=0$ y $x_2(z)=1$
Ninguna de las propuestas es correcta
$x_1(z)=0$ y $x_2(z)=1-z$
¡No! Con $x_2(z)=1$ estaríamos poniendo la cara frontal perpendicular al eje $0X$.
Debes tener en cuenta que en nuestro sólido, el valor máximo de la $x$ para cada $z$ depende de ésta última
Hay una correcta.
En efecto, para cada $z$, el valor mínimo de $x$ es 0 y el valor máximo es $1-z$, ya que el sólido está encajado entre los planos $x=0$ y $x+z=1$. La proyeción de $H$ sobre el plano $XZ$ es
$$R_{xz}=\{(x,z)/\, 0\leq z\leq 1,\, 0\leq x\leq 1-z\}$$
Dibujada en el espacio es
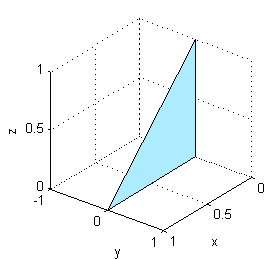

Por último nos encargamos de los límites para la variable $y$. Piensa cuáles serían $y_1(x,z)$ e $y_2(x,z)$ y pulsa en 'Continuar'.
Para cada par $(x,z)$ en la proyección, los valores que puede tomar la $y$ van desde
$$y_1(x,z)=-\sqrt{1-z}$$ a $$y_2(x,z)=\sqrt{1-z}$$
Con todo esto,
$$H=\{(x,y,z)/\, 0\leq z\leq 1,\, 0\leq x\leq 1-z,\, -\sqrt{1-z}\leq y \leq \sqrt{1-z}\}$$
Ahora que tenemos así expresado el conjunto, debemos escribir la integral triple que da la masa de $H$ utilizando las integrales iteradas; ten en cuenta que aquí el orden de integración utilizado no es $dz\, dy\, dx$. Hazlo tú y pulsa en 'Ver'.
Ver
$$\mbox{Masa}(S)=\int_0^1\int_0^{1-z}\int_{-\sqrt{1-z}}^{\sqrt{1-z}} z\, dy\, dx\, dz$$
Paso 4 para el primer orden de integración
Calculamos las integrales iteradas anteriores. Haz las dos primeras tú y pulsa en 'Ver'.
Ver
$$\int_0^1\int_0^{1-z}\int_{-\sqrt{1-z}}^{\sqrt{1-z}} z\, dy\, dx\, dz=2\int_0^1\int_0^{1-z}\int_0^{\sqrt{1-z}} z\, dy\, dx\, dz=$$$$=2\int_0^1\int_0^{1-z} z\sqrt{1-z}\, dx\, dz =2\int_0^1 z(1-z)^{3/2}\, dz$$
Ahora debemos encontar la primitiva de $z(1-z)^{3/2}$. Se trata de una integral irracional que racionalizamos con el cambio de variable $u=(1-z)^{1/2}$. Sigue tú y pulsa en 'Continuar' cuando termines.
$$u=(1-z)^{1/2}\ \ \Rightarrow \ \ z=1-u^2\ \ \Rightarrow \ \ dz=-2u\, du\ \ \Rightarrow \ \ $$
$$\Rightarrow \ \ \int z(1-z)^{3/2}\, dz=-2\int (u^4-u^6)\, du=-2\left(\frac{u^5}{5}-\frac{u^7}{7}\right)+C$$
Deshaciendo el cambio de variable
$$\int z(1-z)^{3/2}\, dz=-\frac{2}{7}(1-z)^{5/2}\left(z+\frac{2}{5}\right)+C$$
Podemos saber ya el valor de la masa:
$$\mbox{Masa}(S)=-2\left.\frac{2}{7}(1-z)^{5/2}\left(z+\frac{2}{5}\right)\right]_0^1=\frac{8}{35}$$
Paso 3 para el segundo orden de integración
Se trata de plantear la integral en el orden $$\mbox{Masa}=\int\!\!\int\!\!\int_H z\, dy\, dz\, dx$$ es decir, proyectando como antes en el plano $XZ$; recuerda que la proyección en ese plano es $$R_{xz}=\{(x,z)/ \, 0\leq z\leq 1,\, 0\leq x\leq 1-z\}$$
Por tanto, sólo tenemos que escribir este conjunto con el otro orden. Pondremos la $x$ entre límites constantes y la $z$ entre dos funciones de $x$. Hazlo tú y pulsa en 'Ver'.
Ver
Es sencillo ver que
$$R_{xz}=\{(x,z)/ \, 0\leq x\leq 1,\, 0\leq z\leq 1-x\}$$
La integral resulta ahora
$$\mbox{Masa}(S)=\int_0^1\int_0^{1-x}\int_{-\sqrt{1-z}}^{\sqrt{1-z}} z\, dy\, dz\, dx$$
Paso 4 para el segundo orden de integración
Cálculo de la integral: haciendo la primera iterada, resulta $$\mbox{Masa}(S)=2\int_0^1\int_0^{1-x} z\sqrt{1-z}\, dz\, dx$$ Encuentra la primitiva de $z\sqrt{1-z}$ utilizando el cambio de variable $u^2=1-z$ y termina la integral.
Ver
$$I=\int z\sqrt{1-z}\, dz=-2\int(u^2-u^4)\, du=-2\left(\frac{u^3}{3}-\frac{u^5}{5}\right)+C=$$
$$=-\frac{2}{5}(1-z)^{3/2}\left(z+\frac{2}{3}\right)$$
y por tanto
$$\mbox{Masa}(S)=2\int_0^1\int_0^{1-x} z\sqrt{1-z}\, dz\, dx=\frac{4}{15}\int_0^1(3x^{5/2}-5x^{3/2}+2)\, dx=\frac{8}{35}$$
Paso 3 para el tercer orden de integración
Debemos encontrar los límites de integración para hacer la integral en el orden $$\mbox{Masa}=\int\!\!\int\!\!\int_H z\, dx\, dz\, dy$$ esto es, proyectando sobre el plano $YZ$ y después sobre el eje $0Y$: $$H=\{(x,y,z)/\, y_1\leq y\leq y_2,\, z_1(y)\leq z\leq z_2(y),\, x_1(y,z)\leq x\leq x_2(y,z)\}$$ Encuentra los límites de integración $y_1$, $y_2$, $z_1(y)$ y $z_2(y)$ y pulsa en 'Ver'.
Ver
La proyección de $H$ sobre el plano $YZ$ es
$$R_{xz}=\{(x,z)/ \, -1\leq y\leq 1,\, 0\leq z\leq 1-y^2\}$$
Dibujada en el espacio resulta
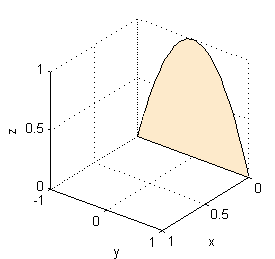

Para cada $(y,z)$ de esa proyección la variable $x$ varía entre $x_1(y,z)$ y $x_2(y,z)$, ¿cuáles son estas funciones?
Ver
En efecto, $x_1(y,z)=0$ y $x_2(y,z)=1-z$. Por tanto,
la región es
$$H=\{(x,y,z)/\, -1\leq y\leq 1,\, 0\leq z\leq 1-y^2,\, 0\leq x\leq 1-z\}$$
y la masa expresada con las integrales iteradas es
$$\mbox{Masa}(S)=\int_{-1}^1\int_0^{1-y^2}\int_0^{1-z} z\, dx\, dz\, dy$$
Paso 4 para el tercer orden de integración
Cálculo de la integral: haciendo la primera iterada, resulta $$\mbox{Masa}(S)=\int_{-1}^1\int_0^{1-y^2} z(1-z)\, dz\, dy$$ Como puedes apreciar, con este orden de integración el cálculo de las primitivas es más sencillo, pues el integrando no resulta irracional. Termina la integral y pulsa en 'Ver'.
Ver
$$\mbox{Masa}(S)=\int_{-1}^1\int_0^{1-y^2} z(1-z)\, dz\, dy= \frac{1}{6}\int_{-1}^1(1-3y^4+2y^6)\, dy=$$
$$=\frac{1}{3}\int_0^1 (1-3y^4+2y^6)\, dy=\frac{8}{35}$$