Enunciado
Considera el problema de valor inicial dado por
$$\frac{dy}{dx}=2-\frac{0.3 y^2}{1.5+x}\hspace{1cm}, \hspace{1cm} y(0)=0.4$$
- Escribe el código que calcula la aproximación mediante el método de Euler del valor de $y(0.5)$ tomando paso $h=0.1$
- Modifica el código anterior para que dé también las aproximaciones en los puntos $x_1=0.1$, $x_2=0.2$, $x_3=0.3$ y $x_4=0.4$ y dibuje la poligonal que aproxima a la solución $y(x)$ para $x$ entre $x=0$ y $x=0.5$
- Podemos intentar mejorar la aproximación tomando un paso menor. Escribe una función para el ordenador, con variable de entrada el valor del paso (éste debe ser divisor de $0.1$) y con salida el vector formado por las aproximaciones de los $y(x_k)$; la función debe también representar la poligonal aproximante.
- Seguimos ganando generalidad: dejaremos ahora como variable el último valor de $x$ al que debemos llegar.
- Generaliza la función anterior para que nos sirva para otras condiciones iniciales: añade la condición inicial a las variables de entrada de la función anterior.
- Por último generaliza la función para que sea aplicable a cualquier problema de la forma
$$\frac{dy}{dx}=f(x,y)\hspace{1cm}, \hspace{1cm} y(x_0)=y_0$$
Resolución del primer apartado
En primer lugar debemos asegurarnos que el método de Euler es aplicable a este caso. Analiza si lo es y pulsa en 'Ver'.
Ver
Para asegurarnos que el problema propuesto tiene solución única debemos acudir al teorema de
existencia y unicidad de solución de un p.v.i de primer orden. En este caso $$f(x,y)=2-\frac{0.3 y^2}{1.5+x}$$
que es una función continua en todo el plano, siendo también continua la derivada parcial respecto de $y$.
Pasamos ya a escribir las líneas con las que este método aproxima $y(0.5)$. Puesto que en este primer apartado no se piden las aproximaciones en los valores intermedios, basta trabajar con dos variables: la $x$ irá guardando los sucesivos valores $0$,$0.1$, $0.2$, $0.3$, $0.4$, $0.5$ y la variable $y$ irá tomando los valores de las aproximaciones en estos puntos.
- Inicializa las variables ...
x=0; y=0.4;
- Utiliza un ciclo 'for' para ir modificando $x$ e $y$ según las ecuaciones recursivas $$\left\{\begin{array}{l}y_{n+1}=y_{n}+hf(x_n,y_n) \\ x_{n+1}=x_n+h\end{array}\right.\ ,\ \ n=0,\, 1,\, 2,\, \ldots$$
for n=1:5
y=y+0.1*(2-0.3*y^2/(1.5+x));
x=x+0.1;
end
- Utiliza 'disp' para mostrar el resultado en la ventana de comandos
disp(['aproximación de y(',num2str(x),')=',num2str(y)])
Ejecutando este código completo se mostrará en la ventana de comandos:
aproximación de y(0.5)=1.3418
Resolución del segundo apartado
En este apartado debemos adaptar el código anterior para que dé los valores de las aproximaciones en los puntos intermedios y represente la poligonal. Si sólo se tratara de ver por pantalla los valores sin dibujar la poligonal, bastaría retirar el punto y coma del final de la línea en la que se actualiza el valor de $y$. Ejecuta
x=0;
y=0.4;
for n=1:5
y=y+0.1*(2-0.3*y^2/(1.5+x))
x=x+0.1;
end
Para mejorar la presentación de los datos, podríamos dejar el punto y coma e introducir un 'disp' en el ciclo:
x=0;
y=0.4;
for n=1:5
y=y+0.1*(2-0.3*y^2/(1.5+x));
x=x+0.1;
disp(['aproximación de y(',num2str(x),')=',num2str(y)])
end
Podíamos representar los vértices de la poligonal, pero no parece la mejor forma de poder dibujarla. Lo que haremos entonces será ir guardando los sucesivos valores de $y$ en un vector según se van calculando. Los valores de $x$ se conocen de antemano, así que se puede generar al principio un vector con ellos.
- genera un vector, 'x', con los valores $0$, $0.1$, $0.2$, $0.3$, $0.4$ y $0.5$
x=0:0.1:0.5;
- define un vector,'y', de la misma longitud que x, cuya primera componente sea $0.4$ (no importa lo que valgan las demás componentes pues se irán actualizando)
y=0.4*ones(size(x));
- escribe un ciclo 'for' que calcule cada nueva aproximación y la guarde en la correspondiente componente de 'y'
for n=1:5
y(n+1)=y(n)+0.1*(2-0.3*y(n)^2/(1.5+x(n)));
end
- utiliza un 'disp' para mostrar en la ventana de comandos del vector 'y' las componentes entre la segunda (que es la aproximación de la solución en $x=0.1$) y la última (que es la aproximación de la solución en $x=0.5$)
disp(['los valores aproximados de y(x) son ',num2str(y(2:6))])
- dibuja la poligonal, marcando los vértices con un asterisco
plot(x,y,'-*')Introduciendo comentarios, todo seguido resulta:
x=0:0.1:0.5; % definición del vector x
y=0.4*ones(size(x)); % definición del vector y
for n=1:5 % ciclo para acutalizar el vector y
y(n+1)=y(n)+0.1*(2-0.3*y(n)^2/(1.5+x(n))); % fórmula y(n+1)=y(n)+h*f(x(n),y(n))
end
disp(['los valores aproximados de y(x) son ',num2str(y(2:6))])
plot(x,y,'-*') % dibujo de la poligonal
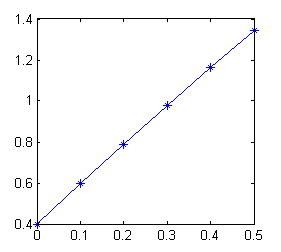
Si ejecutamos este código obtenemos en la ventana de comandos la línea
los valores aproximados de y(x) son 0.5968 0.79012 0.9791 1.1631 1.3418y la figura siguiente:
Resolución del tercer apartado
Tenemos ahora que adaptar el código anterior para que pueda elegirse como valor del paso un divisor de $0.1$ Eso requiere construir una función, cuya variable de entrada sea el valor del paso. ¿Cuál de éstas te parece correcta?
function yaprox=aproxEuler(h)
x=0:h:0.5;
y=0.4*ones(size(x));
for n=1:5
y(n+1)=y(n)+h*(2-0.3*y(n)^2/(1.5+x(n)));
end
yaprox=y(2:6);
plot(x,y,'-*')
end
function yaprox=aproxEuler(h)
nmax=round(0.5/h); % para asegurarnos que nmax es entero
x=0:h:0.5;
y=0.4*ones(size(x));
for n=1:nmax
y(n+1)=y(n)+0.1*(2-0.3*y(n)^2/(1.5+x(n)));
end
yaprox=y(2:end);
plot(x,y,'-*')
end
function aproxEuler(h)
nmax=round(0.5/h); % para asegurarnos que nmax es entero
x=0:h:0.5;
y=0.4*ones(size(x));
for n=1:nmax
y(n+1)=y(n)+h*(2-0.3*y(n)^2/(1.5+x(n)));
end
disp(['los valores aproximados de y(x) son ',num2str(y(2:6))])
plot(x,y,'-*')
end
function yaprox=aproxEuler(h)
nmax=round(0.5/h); % para asegurarnos que nmax es entero
x=0:h:0.5;
y=0.4*ones(size(x));
for n=1:nmax
y(n+1)=y(n)+h*(2-0.3*y(n)^2/(1.5+x(n)));
end
yaprox=y(2:end);
plot(x,y,'-*')
end
El ciclo 'for' no es correcto, ¿por qué 'n' sólo llega hasta 5?
Hay un error en la definición de 'y(n+1)', pues no se refleja que 'h' sea variable.
Esta función es correcta si lo que se quiere es mostrar las aproximaciones en la ventana de comandos. Pero no las guarda en una variable que luego pueda utilizarse, pues no se ha puesto variable de salida.
En efecto, esa función cumpliría con lo que se pide en este apartado. Podemos testarla con el paso trabajado en los apartados anteriores y comprobar que el resultado es el mismo. Para ello pondríamos en la ventana de comandos
>> yaprox=aproxEuler(.1)con el resultado
yaprox =
0.5968 0.7901 0.9791 1.1631 1.3418
Para reducir el paso a la mitad, ejecutamos
>> yaprox=aproxEuler(.05)obteniendo
yaprox =
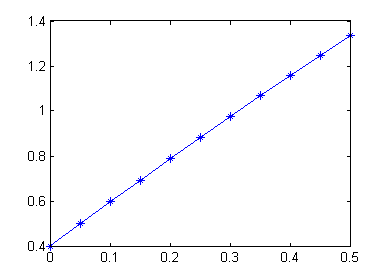
0.4984 0.5960 0.6927 0.7883 0.8828 0.9761 1.0682 1.1589 1.2483 1.3364
y la poligonal
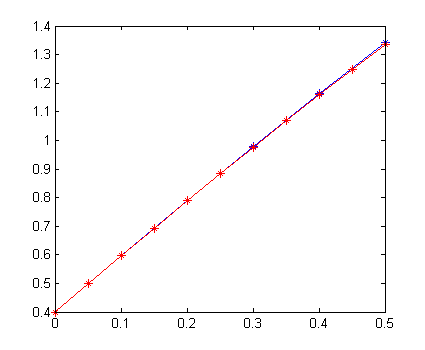
Resolución del cuarto apartado
Añadimos una variable de entrada a la función anterior, para que sirva en la aproximación de la solución en cualquier valor. Escribe la nueva función y pulsa en 'Ver' cuando la tengas.
Ver
Solamente hemos de modificar las tres primeras líneas de la función anterior: la declaración de la función, el cálculo del número de iteraciones ('nmax') y la definición del vector 'x'.
function yaprox=aproxEuler(h,xf)
nmax=round(xf/h);
x=0:h:xf;
y=0.4*ones(size(x));
for n=1:nmax
y(n+1)=y(n)+h*(2-0.3*y(n)^2/(1.5+x(n)));
end
yaprox=y(2:end);
plot(x,y,'-*')
end
Podemos testar esta función ejecutando
>> yaprox=aproxEuler(0.05,0.5)que debe reproducir la última ejecución realizada en el apartado anterior.
Resolución del quinto apartado
¿Si la condición inicial fuera otra? Con objeto de que nos sirva para resolver un problema de valor inicial de la forma $$\frac{dy}{dx}=2-\frac{0.3 y^2}{1.5+x}\hspace{1cm}, \hspace{1cm} y(x_0)=y_0$$ ¿cuántos cambios deben hacerse en la función del apartado anterior?
Habrá que cambiar cinco líneas
Habrá que cambiar tres líneas
Habrá que cambiar cuatro líneas
Creo que con menos bastaría.
Demasiado pocas.
Hemos de modificar las cuatro primeras líneas de la función anterior: la declaración de la función, el cálculo del número de iteraciones ('nmax') y las definiciones de los vectores 'x' e 'y'.
Actualízalas y pulsa en 'Continuar' cuando lo tengas.
function yaprox=aproxEuler(h,x0,y0,xf)
nmax=round((xf-x0)/h);
x=x0:h:xf;
y=y0*ones(size(x));
for n=1:nmax
y(n+1)=y(n)+h*(2-0.3*y(n)^2/(1.5+x(n)));
end
yaprox=y(2:end);
plot(x,y,'-*')
end
Para reproducir la última ejecución escribiremos
>> yaprox=aproxEuler(0.05,0,0.4,0.5)
Resolución del sexto apartado
Finalmente lo único que nos queda por generalizar es la ecuación diferencial de primer orden, de forma que en este apartado escribiremos una función que permita aproximar por el método de Euler la solución del problema de valor inicial $$\frac{dy}{dx}=f(x,y)\hspace{1cm}, \hspace{1cm} y(x_0)=y_0$$ Obviamente deberemos introducir una nueva variable, que llamaremos 'f', en la lista de variables de entrada, y utilizarla después en el ciclo 'for'. Incorpora estos cambios en la función y pulsa en 'Ver' cuando lo tengas.
Ver
function yaprox=aproxEuler(f,h,x0,y0,xf)
nmax=round((xf-x0)/h);
x=x0:h:xf;
y=y0*ones(size(x));
for n=1:nmax
y(n+1)=y(n)+h*f(x(n),y(n));
end
yaprox=y(2:end);
plot(x,y,'-*')
end
Hemos dado por supuesto que la función de dos variables, 'f', puede evaluarse directamente. Eso es así si se ha definido como una función utilizando el '@'; por ejemplo, las dos líneas
>> f=@(x,y) 2-0.3*y^2/(1.5+x); >> yaprox=aproxEuler(f,0.05,0,0.4,0.5)reproducirían el ya conocido resultado de los apartados anteriores.