Enunciado
Un gas circula alrededor de una curva $C_a$ según el campo de velocidades
$${\bf V}=(\mbox{sen}\, x^2-\cos y,x\,\mbox{sen}\,y+\frac{x^2y^2}{2a^4})$$
Cada curva $C_a$ es la unión de la circunferencia de centro $(1,0)$ y radio 1 y la circunferencia de centro $(\frac{a}{2},0)$ y radio $\frac{a}{2}$. La única condición para el valor de $a$ es que $a>2$.
Para $a=3$, una muestra de vectores de ${\bf V}$ sobre $C_3$ sería
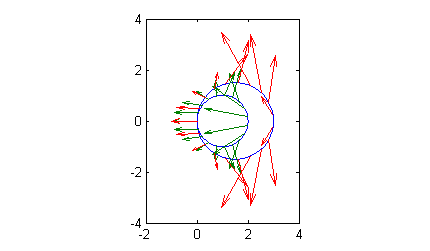
- A la vista de esa figura ¿puedes conjeturar el signo de la circulación del gas alrededor de una curva $C_a$? Halla el valor de la circulación alrededor de la curva $C_a$ y comprueba la veracidad de tu conjetura.
- Prepara una función para el ordenador que dibuje la curva $C_a$ y una muestra de $m$ vectores en cada circunferencia que la compone; las variables de entrada de esta función serán por tanto $a$ y $m$.
- ¿A qué tiende el valor de la velocidad media del gas en los puntos de $C_a$? Dibuja en el ordenador la gráfica de los valores de esa velocidad media frente a los valores de $a$ entre $2$ y $10$.
- ¿Qué valor de $a$ debe tomarse para que la velocidad media en los puntos de la curva $C_a$ sea $v=.0055$?
Resolución del primer apartado
Una de las interpretaciones de la integral de un campo vectorial sobre una curva es como circulación de un fluido alrededor de una curva: $$\mbox{circulación}=\oint_{C_a} {\bf V}\cdot d{\bf r}$$ Esta circulación es positiva si la tendencia del fluido es a girar en el sentido positivo de la curva (antihorario); en este caso observamos que los vectores velocidad ayudarían al movimiento en algunos puntos pero en otros actúan en contra de ese giro; por tanto no se puede conjeturar si la circulación es positiva o es negativa. Para hallarla $\ldots$
Utilizamos el teorema sobre campos conservativos
Parametrizamos $C_a$, hallamos $d{\bf r}$, $\ldots$
Utilizamos el teorema de Green
No sabes si el campo es conservativo, de hecho no lo es.
Puede ser que la integral simple que resulta te la haga el ordenador, pero en principio hay otra propuesta mejor.
En efecto, parece que utilizar el teorema de Green pueda simplificar el cálculo, ya que
$$N'_x-M'_y$$ es $\ldots$ (pulsa en 'Continuar' cuando lo calcules)
$$N'_x-M'_y=\frac{xy^2}{a^4}$$
esto es, una función mucho más simple que la $M$ y la $N$. Veamos que se cumplen las condiciones del teorema de Green. Compruébalas, escribe la región encerrada por $C_a$ utilizando coordenadas polares y pulsa en 'Ver'.
Ver
Para poder expresar la región encerrada por $C_A$ en coordenadas polares escribimos las ecuaciones de las circunferencias que la forman:
- $$(x-1)^2+y^2=1\hspace{.4cm}\Rightarrow \hspace{.4cm} r=2\cos \theta, \hspace{.3cm} \theta\in[-\frac{\pi}{2},\frac{\pi}{2}]$$
- $$(x-\frac{a}{2})^2+y^2=\frac{a^2}{4}\hspace{.4cm}\Rightarrow \hspace{.4cm} r=a\cos \theta, \hspace{.3cm} \theta\in[-\frac{\pi}{2},\frac{\pi}{2}]$$
Según la tesis del teorema de Green,
$$\mbox{circulación}=\oint_{C_a} {\bf V}\cdot d{\bf r}=\int\!\!\int _{S_a} (N'_x-M'_y)\, dA$$
así que escrita en polares, la integral anterior es
$$\mbox{circulación}=\frac{1}{a^4}\int_{-\pi/2}^{\pi/2}\int_{2\cos\theta}^{a\cos\theta}
r^3\cos\theta\, \mbox{sen}^2\,\theta\, dr\, d\theta$$
Ninguna de las propuestas es correcta.
$$\mbox{circulación}=\frac{2}{a^4}\int_0^{\pi/2}\int_{2\cos\theta}^{a\cos\theta}
r^4\cos\theta\, \mbox{sen}^2\,\theta\, dr\, d\theta$$
Creo que en el integrando se te olvida algo.
Hay una correcta.
En efecto, hemos utilizado que $dA=r\,d\theta\, dr$ y que la función $N'_x-M'_y$ es simétrica par respecto de la variable $y$, así como la región de integración $S_a$ es simétrica respecto del eje $y=0$. La integral en la variable $r$ es inmediata, al hacerla resulta $\ldots$ haz la integral iterada primera y pulsa en 'Continuar'.
$$\mbox{circulación}=\frac{2}{5a^4}(a^5-32)\int_0^{\pi/2}
\cos^6\theta\, \mbox{sen}^2\,\theta\, d\theta$$
La integral trigonométrica
$$\int \cos^6\theta\, \mbox{sen}^2\,\theta\, d\theta $$
se transforma en la racional $$\int \frac{t^2}{(1+t^2)^5}\, dt$$ con el cambio de variable $\mbox{tg}\, \theta=t$. La racional puede resolverse, por ejemplo con el método de Hermite. Si nos queremos ahorrar estas cuentas, podemos hacer la integral trigonométrica en el ordenador:
syms u int((cos(u))^6*(sin(u))^2,u,0,pi/2)que nos da $$\int_0^{\pi/2} \cos^6\theta\, \mbox{sen}^2\,\theta\, d\theta=\frac{5}{256}\pi$$ con lo cual $$\mbox{circulación}=\frac{2}{5a^4}(a^5-32)\frac{5}{256}\pi= \frac{\pi}{128}\frac{a^5-32}{a^4}$$ que es un número positivo para cualquier $a>2$.
Resolución del segundo apartado
Para dibujar la curva en el ordenador y una muestra de vectores, utilizaremos para $C_a$ las ecuaciones paramétricas $$x(t)=2\cos^2 t ,\hspace{.3cm} y(t)=2\cos t\,\mbox{sen}\, t ,\hspace{.3cm} t\in[-\frac{\pi}{2},\frac{\pi}{2}]$$ para la circunferencia interior y $$x(t)=a\cos^2 t ,\hspace{.3cm} y(t)=a\cos t\,\mbox{sen}\, t ,\hspace{.3cm} t\in[-\frac{\pi}{2},\frac{\pi}{2}]$$ para la exterior. En el fichero curvaycampo.m preparamos la función, siguiendo los pasos que se presentan a continuación; en cada uno, pulsa en 'Continuar' cuando lo hayas hecho.- Declara la función con sus variables de entrada.
function curvaycampo(a,m)
- define un vector de parámetros para dibujar cada circunferencia
t=-pi/2:pi/50:pi/2; % vector de parámetros
- define las coordenadas de la circunferencia interior; dibújala
R=2*cos(t); x=R.*cos(t); y=R.*sin(t); % circunferencia interior plot(x,y) % trazado de la circunferencia interior
- repite para la circunferencia exterior y fija igual escala en ambos ejes
hold on R=a*cos(t); x=R.*cos(t); y=R.*sin(t); % circunferencia exterior plot(x,y) axis equal
- Comenzamos con el trazado de vectores del campo; define un vector de parámetros de m componentes entre $\frac{-\pi}{2}$ y $\frac{\pi}{2}-\frac{\pi}{m}$ (esto lo hacemos así porque el punto de las curvas correspondiente a $\frac{-\pi}{2}$ y a $\frac{\pi}{2}$ es el mismo);
tv=linspace(-pi/2,pi/2-pi/m,m) ;
- define las coordenadas correspondientes a esos parámetros para la circunferencia interior y dibuja con quiver los correspondientes vectores
R=2*cos(tv);x=R.*cos(tv); y=R.*sin(tv); % circunferencia interior quiver(x,y,sin(x.^2)-cos(y),x.*sin(y)+x.^2.*y.^2/(2*a^4),0) % vectores del campo sobre la circ. interior
- repite para la circunferencia exterior; puedes fijar que los dibuje en rojo; cierra la función
R=a*cos(tv); x=R.*cos(tv); y=R.*sin(tv); % circunferencia interior quiver(x,y,sin(x.^2)-cos(y),x.*sin(y)+x.^2.*y.^2/(2*a^4),0,'r') hold off endCon esto, nuestro fichero tendrá las siguientes líneas, a las que habría que añadir, despues de la línea de definición de la función, unas líneas de comentario sobre lo que hace esta función:
function curvaycampo(a,m) % .... lineas explicativas de lo que hace la función % %%%%%%% trazado de la curva t=-pi/2:pi/50:pi/2; % vector de parámetros R=2*cos(t); x=R.*cos(t); y=R.*sin(t); % circunferencia interior plot(x,y) hold on R=a*cos(t); x=R.*cos(t); y=R.*sin(t); % circunferencia exterior plot(x,y) axis equal % %%%%%%% muestra del campo vectorial tv=linspace(-pi/2,pi/2-pi/m,m) ; % vector de valores del parámetro R=2*cos(tv);x=R.*cos(tv); y=R.*sin(tv); % circunferencia interior quiver(x,y,sin(x.^2)-cos(y),x.*sin(y)+x.^2.*y.^2/(2*a^4),0) % vectores del campo sobre la circ. interior R=a*cos(tv); x=R.*cos(tv); y=R.*sin(tv); % circunferencia interior quiver(x,y,sin(x.^2)-cos(y),x.*sin(y)+x.^2.*y.^2/(2*a^4),0,'r') hold off end
Resolución del tercer apartado
La velocidad media en los puntos de la curva se obtiene como el cociente entre la integral del campo de velocidades a lo largo de la curva (la circulación que acabas de calcular) y la longitud de la curva. La longitud de la curva $C_a$ la calculamos como suma de las longitudes de dos circunferencias: $$\mbox{longitud}(C_a)=(2+a)\pi$$ y por tanto la velocidad media es $$v_m(a)=\frac{a^5-32}{128a^4(2+a)}$$ que tiende a parecerse $\frac{1}{128}=0.0078$ cuando vamos tomando valores crecientes de $a$.Escribe las órdenes necesarias para dibujar la gráfica de $v_m(a)$ para $a$ entre 2 y 10. Pulsa en 'Ver' cuando lo tengas.
Ver
Con
a=linspace(2,10,50);
plot(a,(a.^5-32)./(128*a.^4.*(a+2)))
xlabel('a');ylabel('v_m(a)')
obtenemos
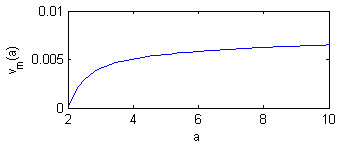
Resolución del cuarto apartado
Debemos hallar el valor de $a$ para el cual la velocidad media en los puntos de la curva $C_a$ sea $v=.0055$: $$\frac{a^5-32}{128a^4(2+a)}=v \hspace{.4cm}\Rightarrow \hspace{.4cm} (128v-1)a^5+256va^4+32=0$$ Piensa cómo utilizar el ordenador para resolver esa ecuación y luego pulsa en 'Ver'.
Ver
Una opción es utilizar el comando 'solve':
v=.0055; syms a solve((128*v-1)*a^5+256*v*a^4+32)que nos dará las cinco raíces de esa ecuación; observamos que sólo una es real: $a=4.9385$. Otra opción, puesto que la ecuación que hay que resolver es polinómica, es utilizar el comando 'roots':
v=.0055; p=[(128*v-1) 256*v 0 0 0 32]; roots(p)que obviamente aportará las mismas soluciones.