Índice de tema

 

Enunciado

Dado ${\bf F}(x,y,z)=n\rho^{n-2}{\bf r}$, con
  • $n\in {\bf N}$
  • ${\bf r}(x,y,z)$ el vector de posición del punto $P(x,y,z)$
  • $\rho=|{\bf r}|$
  1. Prueba que ${\bf F}$ es conservativo.
  2. Dibuja en el ordenador una muestra de ${\bf F}$, para $n=4$, en puntos del cubo $[1,2]\times[1,2]\times[1,2]$
  3. Si $f(x,y,z)$ es un campo escalar tal que $\nabla f={\bf F}$ y $f(0,1,0)=3$, encuentra el valor de $f(1,0,2)$ sin determinar el campo $f(x,y,z)$.
  4. Comprueba el resultado anterior determinando el campo $f(x,y,z)$.
  5. Dibuja varias secciones del cubo $[0,1]\times[0,1]\times[0,2]$ coloreadas según el campo $f(x,y,z)$ tomando $n=4$, calculado en el apartado anterior.

Resolución del primer apartado

Para probar que ${\bf F}$ es conservativo, comprobaremos que su rotacional es nulo, es decir $$\frac{\partial P}{\partial y}=\frac{\partial N}{\partial z} \ \ ,\ \ \frac{\partial M}{\partial z}=\frac{\partial P}{\partial x} \ \ ,\ \ \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}$$ siendo $M$, $N$ y $P$ las componentes del campo. Hemos por tanto de empezar encontrando esas componentes. Sustituye $\rho$ y ${\bf r}$ en la expresión de ${\bf F}$ para encontrarlas y pulsa en 'Ver' cuando lo tengas.
Ver
$${\bf F}(x,y,z)=n\rho^{n-2}{\bf r}=n(x^2+y^2+z^2)^{(n-2)/2}(x,y,z)=(M,N,P)\hspace{.3cm} \Rightarrow \hspace{.3cm} $$ $$ \left\{\begin{array}{l} M=n(x^2+y^2+z^2)^{(-1+n/2)}x \\ N=n(x^2+y^2+z^2)^{(-1+n/2)}y \\ P=n(x^2+y^2+z^2)^{(-1+n/2)}z \end{array}\right.$$
Comprueba ahora que $\frac{\partial P}{\partial y}=\frac{\partial N}{\partial z}$ y pulsa en 'Ver'.
Ver
Derivando, $$\frac{\partial P}{\partial y}=n(n-2)(x^2+y^2+z^2)^{(-2+n/2)}yz$$ $$\frac{\partial N}{\partial z}=n(n-2)(x^2+y^2+z^2)^{(-2+n/2)}yz$$ que efectivamente son iguales. Por simetría, o haciendo las correspondientes derivadas, comprobamos que se verifican las otras dos igualdades. Por tanto, el campo es conservativo.

Resolución del segundo apartado

Para dibujar una muestra de vectores escribiremos las líneas necesarias para
  • generar una malla de puntos en el cubo
  • generar las componentes del campo sobre los puntos de la malla
  • dibujar los vectores (con quiver3)
Intenta cumplimentar estos pasos y pulsa en 'Ver'
Ver 
[X,Y,Z]=meshgrid(1:.25:2); % malla de puntos en el cubo
R=4*(X.^2+Y.^2+Z.^2);      % parte común a las tres componentes
M=R.*X;					   % primera componente del campo
N=R.*Y;					   % segunda componente del campo
P=R.*Z;					   % tercera componente del campo
quiver3(X,Y,Z,M,N,P)	   % trazado de los vectores
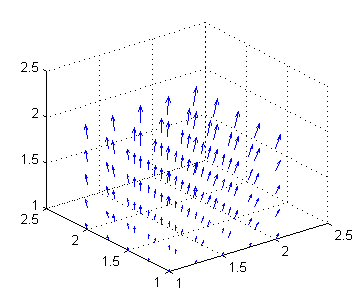
Gráfica

Resolución del tercer apartado

Para resolver este apartado haremos uso del teorema fundamental de integrales de línea. Llamamos $C$ a una curva que va desde el punto $(0,1,0)$ hasta el punto $(1,0,2)$; aplicando ese teorema sabemos que
$$\int_C \nabla f\cdot d{\bf r} =f(0,1,0)-f(1,0,2)$$
ninguna de las propuestas es correcta
$$\int_C \nabla f\cdot d{\bf r} =f(1,0,2)-f(0,1,0)$$
No, mira bien el teorema.
Sí hay una correcta.
En efecto, así es. De manera que $$f(1,0,2)=\int_C \nabla f\cdot d{\bf r} +f(0,1,0)$$ con lo cual, tendremos calculado $f(1,0,2)$ si conocemos $$W=\int_C \nabla f\cdot d{\bf r}$$ con la facilidad de poder elegir la curva $C$ que nos parezca más sencilla.
Podemos tomar por ejemplo el segmento recto que une esos dos puntos (otra opción razonable es ir por una poligonal). Una opción fácil para parametrizar el segmento es utilizar el vector director, que es
ninguno de los propuestos es correcto
$$(-1,1,-2)$$
$$(1,-1,2)$$
Sí hay uno correcto.
No es ése, míralo bien.
Ése es el vector director. Unas ecuaciones paramétricas para $C$ son $$C:\left\{\begin{array}{l}x=t \\ y=1-t \\ z=2t \end{array}\right.\hspace{.3cm}, \hspace{.3cm}t\in[0,1]$$ o escrita en notación vectorial $${\bf r}(t)=(t,1-t,2t)\hspace{.3cm}, \hspace{.3cm}t\in[0,1]$$
Escribe ahora la composición ${\bf F}({\bf r}(t))$, y pulsa en 'Ver'.
Ver
Puesto que $x^2+y^2+z^2=t^2+(1-t)^2+(2t)^2=6t^2-2t+1$, $${\bf F}({\bf r}(t))=n(6t^2-2t+1)^{(-1+n/2)}(t,1-t,2t)$$
Entonces,
$$W=\int_0^1 {\bf F}({\bf r}(t))\, ds=\int_0^1 {\bf F}({\bf r}(t)) \sqrt{6} \, dt$$
$$W=\int_0^1 {\bf F}({\bf r}(t))\cdot (dx,dy,dz)$$
¡Barbaridad! Míralo bien.
Correcto. Evalúa ese producto escalar del integrando y pulsa en 'Continuar'.
$${\bf F}({\bf r}(t))\cdot (dx,dy,dz)=n(6t^2-2t+1)^{(-1+n/2)}(t,1-t,2t)\cdot (1,-1,2)\, dt=$$ $$=n(6t^2-2t+1)^{(-1+n/2)}(6t-1)\, dt$$ Calcula ahora la integral y pulsa en 'Ver'.
Ver
$$W=n\int_0^1 (6t^2-2t+1)^{(-1+n/2)}(6t-1)\, dt=\left.\frac{n}{2}(\frac{n}{2}-1+1)^{-1}(6t^2-2t+1)^{n/2}\right]_0^1=$$ $$=\left.(6t^2-2t+1)^{n/2}\right]_0^1=5^{n/2}-1$$ Con este valor de $W$, determinamos $f(1,0,2)$: $$f(1,0,2)=5^{n/2}-1+3=5^{n/2}+2$$ En la siguiente figura puedes ver una muestra de vectores del campo (tomando $n=4$), sobre puntos de ese segmento; puedes observar que el campo trabaja siempre a favor del movimiento desde $(0,1,0)$ a $(1,0,2)$, luego la integral de línea debía necesariamente resultar un número positivo; debajo se incluye el código con el que se ha generado la figura.
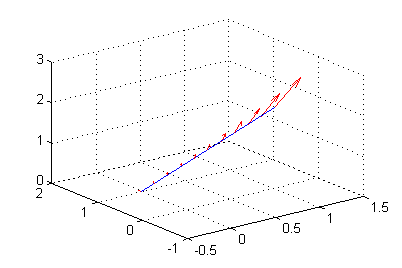
Gráfica
t=0:.1:1;  % vector de parámetros
X=t; Y=1-t;Z=2*t; % coordenadas de los puntos donde se colocarán los vectores
% se definen las componentes del campo sobre los puntos anteriores:
R=4*(X.^2+Y.^2+Z.^2);
M=R.*X;
N=R.*Y;
P=R.*Z;
quiver3(X,Y,Z,M,N,P,'r') % trazado de los vectores
hold on
plot3([0 1],[1 0],[0 2]) % trazado del segmento
hold off

Resolución del cuarto apartado

Tenemos que encontrar $f$, la función potencial de $${\bf F}=n(x^2+y^2+z^2)^{-1+n/2}(x,y,z)$$ para la cual $f(0,1,0)=3$. En primer lugar utilizamos que $$\frac{\partial f}{\partial x}=n(x^2+y^2+z^2)^{-1+n/2}x$$ Al integrar en $x$, tendremos que
$$f(x,y,z)=(x^2+y^2+z^2)^{n/2}$$
La propuesta no es correcta
Esa sería una $f$ que cumple la condición de la derivada parcial, pero no la única. De hecho, no cumple que $f(0,1,0)=3$.
En efecto, la propuesta no es correcta. Lo correcto es poner $$f(x,y,z)=(x^2+y^2+z^2)^{n/2}+K(y,z)$$ donde $K(y,z)$ es la constante de integración en $x$, pero función de $y$ y $z$.
Lo que ocurre en este caso es que el problema es simétrico en las tres variables, luego tendremos que $$f(x,y,z)=(x^2+y^2+z^2)^{n/2}+K$$ Sólo falta ya encontrar el valor de la constante $K$. Hállala y pulsa en 'Ver'.
Ver
Utilizando que $f(0,1,0)=3$ sabemos que $K=2$, luego la función potencial buscada es $$f(x,y,z)=(x^2+y^2+z^2)^{n/2}+2$$ que cumple el resultado del apartado anterior: $$f(1,0,2)=5^{n/2}+2$$

Resolución del cuarto apartado

Para dibujar varias secciones del cubo $[0,1]\times[0,1]\times[0,2]$ seguiremos los siguientes pasos
  • generar una malla de puntos en el cubo
  • definir un vector con los valores de x para las secciones x cte; idem para los otros ejes
  • dibujar las secciones (con slice)
Intenta cumplimentar estos pasos y pulsa en 'Ver'
Ver 
[X,Y,Z]=meshgrid(0:.05:1,0:.05:1,0:.1:2); % malla de puntos en el cubo
secx=.25:.25:1; 					%valores de x para secciones x=cte
secy=secx;  						%valores de y para secciones x=cte
secz=0:.5:1.5; 						%valores de z para secciones x=cte
slice(X,Y,Z,(X.^2+Y.^2+Z.^2).^2+2,secx,secy,secz) % dibujo de las secciones
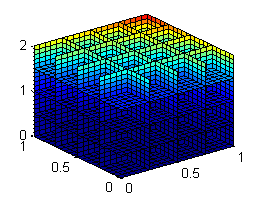
Gráfica

Resumen

  1. Comprobar la igualdad de las derivadas cruzadas de las componentes del campo
    • Utilizar el teorema fundamental de integrales de línea
    • Evaluar el trabajo realizado por el campo sobre una curva que una los dos puntos, se elige el segmento que los une
    • Encontrar todo el conjunto de funciones potenciales integrando las componentes del campo
    • Determinar la función potencial que se ajusta a la condición del ejercicio.