Longitud y masa de un alambre

Enunciado

Suponemos que un alambre se coloca en la curva $C_a$ intersección de la esfera $x^2+y^2+z^2=R^2$ con el plano $x+z=a$, siendo $R$ y $a$ constantes tales que $0\leq a< \sqrt{2}R$.

Encuentra una parametrización de $C_a$.

Escribe una función para el ordenador que dibuje varias curvas $C_a$ de estas características, correspondientes a tantos valores de $a$.

Encuentra la longitud de $C_a$.

Halla la masa del alambre si la función de densidad lineal es
$f(x,y,z)=x^2+y^2+z^2$

$f(x,y,z)=(x-R/\sqrt{2})^2+y^2+(z-R/\sqrt{2})^2$

$f(x,y,z)=(x+R/\sqrt{2})^2+y^2+(z+R/\sqrt{2})^2$

$f(x,y,z)=(x+R/\sqrt{2})^2+y^2+(z-R/\sqrt{2})^2$

y analiza en cada caso para qué valor de $a$ el valor medio de la densidad del alambre es mínimo y para qué valor es máximo.

Resolución del primer apartado

En primer lugar sustituimos $z=a-x$ en la ecuación de la esfera y buscamos, completando cuadrados, la ecuación de una elipse. Inténtalo y pulsa después en 'Ver'.

Ver

$$x^2+y^2+(a-x)^2=R^2 \hspace{.3cm}\Rightarrow \hspace{.3cm} x^2-ax+\frac{1}{2}y^2=\frac{1}{2}(R^2-a^2)$$ completando cuadrados y llamando $b=\sqrt{2R^2-a^2}/2$, esta expresión se escribe $$\left(\frac{x-\frac{a}{2}}{b}\right)^2+\left(\frac{y}{\sqrt{2}b}\right)^2=1$$ pero no olvidemos que está en el plano $x+z=a$. Ahora podemos parametrizar fácilmente esta elipse utilizando como parámetro $t\in[0,2\pi]$. Hazlo tú y pulsa en 'Continuar'

Tomaremos como parametrización de la curva $C_a$ la siguiente $$C_a:\hspace{.3cm}\left\{\begin{array}{l} x=\frac{a}{2}+b\cos t \\ y=\sqrt{2}b\,\mbox{sen}\, t \\ z=\frac{a}{2}-b\cos t \end{array}\right.\hspace{.3cm}, \hspace{.4cm}t\in[0,2\pi]$$

Resolución del segundo apartado

Prepararemos una función, llamada aros, con dos variables de entrada

R: radio de la esfera
num: número de curvas que se trazarán

para que dibuje num aros correspondientes a num valores de $a$ intermedios a 0 y $\sqrt{2}R$. Seguiremos los pasos que se presentan a continuación. En cada uno, pulsa en 'Continuar' cuando lo hayas completado.

Declara la función con sus dos variables de entrada

function aros(R,num)

genera un vector de longitud num+1, llamado 'a', que comience en 0 y termine en $\sqrt{2}R$

a=linspace(0,sqrt(2)*R,num+1);

genera el vector 'b' con los correspondientes valores de $b$

b=sqrt(2*R^2-a.^2)/2;

genera un vector,'t', de valores del parámetro t

t=0:pi/30:2*pi;

escribe un ciclo for para dibujar cada curva, según la parametrización del apartado anterior

for k=1:num
   plot3(a(k)/2+b(k)*cos(t),sqrt(2)*b(k)*sin(t),a(k)/2-b(k)*cos(t))
   hold on
end
hold off

por último, añade el mallado en los planos coordenados, pon nombre a los ejes, fija [137,30] como punto de vista y cierra la función

grid on
xlabel('x');ylabel('y');zlabel('z');
view([137,30])
end

Toda la función, añadiendo comentarios y ayuda inicial, resulta

function aros(R,num)
% dibuja num aros contenidos en la esfera x^2+y^2+z^2=R^2
% todos ellos intersecciones con planos de la forma x+z=c,
% tomando c num valores intermedios (incluidos éstos) a 0 y sqrt(2)R
% ya que este valor es el máximo que puede tomar c para que exista intersección
% (la intersección correspondiente a c=sqrt(2)R es un único punto)
a=linspace(0,sqrt(2)*R,num+1);  % vector con los valores de la constante c
b=sqrt(2*R^2-a.^2)/2;  % valores de b correspondientes
t=0:pi/30:2*pi; % vector de parámetros
for k=1:num  % ciclo para dibujar cada aro
   plot3(a(k)/2+b(k)*cos(t),sqrt(2)*b(k)*sin(t),a(k)/2-b(k)*cos(t))
   hold on
end
hold off
grid on  % mallado de los planos coordenados
xlabel('x');ylabel('y');zlabel('z'); % etiquetas para los ejes
view([137,30])  % punto de vista
end

Por ejemplo, ejecutando

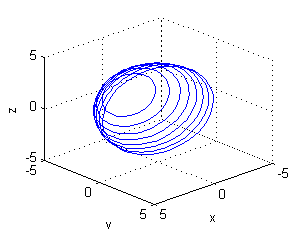
>> aros(4,8)

obtendremos
Gráfica

Resolución del tercer apartado

Para hallar la calcular la longitud de un alambre, debemos encontrar el elemento diferencial de arco. Hazlo tú y pulsa en 'Ver'.

Ver

$$C:\hspace{.3cm}\left\{\begin{array}{l} x=\frac{a}{2}+b\cos t \\ y=\sqrt{2}b\,\mbox{sen}\, t \\ z=\frac{a}{2}-b\cos t \end{array}\right.\hspace{.3cm}\Rightarrow \hspace{.4cm}\left\{\begin{array}{l} x'=-b\,\mbox{sen}\, t \\ y'=\sqrt{2}b\cos t \\ z'=b\,\mbox{sen}\, t \end{array}\right.\hspace{.3cm}\Rightarrow \hspace{.4cm} ds=\sqrt{2}b\, dt$$

La longitud de $C_a$ es por tanto $$\mbox{longitud}(C_a)=\int_{C_a} ds=\sqrt{2}b\int_0^{2\pi} dt=2\sqrt{2}\pi b=\sqrt{2}\pi\sqrt{2R^2-a^2}$$

Resolución del cuarto apartado

Debemos ahora utilizar que la masa de un alambre puede calcularse haciendo la integral de la densidad sobre la curva que forma el alambre.

densidad lineal: $f(x,y,z)=x^2+y^2+z^2$

Ver

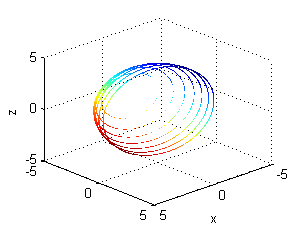
$$f(x(t),y(t),z(t))=R^2\hspace{.3cm}\Rightarrow \hspace{.4cm} \mbox{masa}=R^2\int_{C_a} ds =\sqrt{2}\pi R^2\sqrt{2R^2-a^2}$$ Observa que en este caso la densidad es el cuadrado de la distancia al origen de coordenadas, así que es obvio que todos los puntos de cada aro tengan la misma densidad: $R^2$, de manera que su masa es esa densidad constante por su longitud. El valor medio de la densidad a lo largo de $C_a$ es obviamente $$f_m=R^2$$ igual para todos los valores de $a$. Si dibujamos los aros con una pequeña anchura y los coloreamos según el valor de la densidad lineal, obtendremos
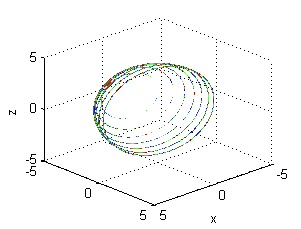
Gráfica

Repetimos el proceso para la siguiente función de densidad:

densidad lineal: $f(x,y,z)=(x-R/\sqrt{2})^2+y^2+(z-R/\sqrt{2})^2$

Ver

$$f(x(t),y(t),z(t))=2\left(\frac{a}{2}-\frac{R}{\sqrt{2}}\right)^2+2b^2=2R^2-\sqrt{2}aR \hspace{.3cm}\Rightarrow \hspace{.4cm}$$ $$\Rightarrow \hspace{.4cm} \mbox{masa}=\int_{C_a}f\, ds =(2R^2-\sqrt{2}aR)\mbox{longitud}$$ Observa que en este caso la densidad es el cuadrado de la distancia al punto $P(\frac{R}{\sqrt{2}},0,\frac{R}{\sqrt{2}})$; todos los puntos de cada aro tienen la misma densidad, de manera que su masa es esa densidad constante por su longitud. El valor medio de la densidad a lo largo de $C_a$ es $$f_m=2R^2-\sqrt{2}aR$$ que es máximo para $a=0$ (aro de mayor longitud y más alejado de $P$) y va decreciendo cuanto mayor sea $a$. Si dibujamos los aros con una pequeña anchura y los coloreamos según el valor de la densidad lineal, obtendremos
Gráfica

Tomamos ahora como densidad el cuadrado de la distancia al punto $Q(-\frac{R}{\sqrt{2}},0,-\frac{R}{\sqrt{2}})$.

densidad lineal: $f(x,y,z)=(x+R/\sqrt{2})^2+y^2+(z+R/\sqrt{2})^2$

Será máxima para $a=0$ e irá decreciendo con el valor de $a$.

No ocurrirá ninguna de las dos opciones propuestas.

Será mínima para $a=0$ e irá creciendo con el valor de $a$.

No, pues el aro correspondiente a $a=0$ es el que tiene los puntos con menor densidad.

Una de las dos es correcta.

En efecto, hagamos las cuentas para comprobarlo: $$f(x(t),y(t),z(t))=2\left(\frac{a}{2}+\frac{R}{\sqrt{2}}\right)^2+R^2-\frac{a^2}{2}=2R^2+\sqrt{2}aR \hspace{.3cm}\Rightarrow $$ $$ \Rightarrow \hspace{.4cm} \mbox{masa}=\int_{C_a}f\, ds =(2R^2+\sqrt{2}aR)\mbox{longitud}$$ El valor medio de la densidad a lo largo de $C_a$ es $$f_m=2R^2+\sqrt{2}aR$$ que es mínimo para $a=0$ (aro más cercano a $Q$) y va creciendo cuanto mayor sea $a$. 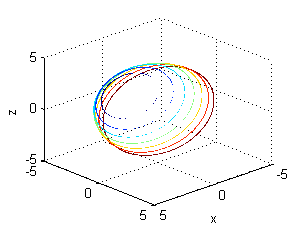Si dibujamos los aros con una pequeña anchura y los coloreamos según el valor de la densidad lineal, obtendremos
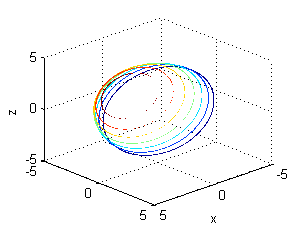
Gráfica

Por último hemos de considerar como densidad el cuadrado de la distancia al punto $H(-\frac{R}{\sqrt{2}},0,\frac{R}{\sqrt{2}})$.

densidad lineal: $f(x,y,z)=(x+R/\sqrt{2})^2+y^2+(z-R/\sqrt{2})^2$

Ver

$$f(x(t),y(t),z(t))=2R^2+4b\frac{R}{\sqrt{2}}\cos t \hspace{.3cm}\Rightarrow \hspace{.4cm} $$ $$\mbox{masa}=\int_{C_a}f\, ds =2\sqrt{2}b\int_0^{2\pi} \left(R^2+\frac{2}{\sqrt{2}}bR\cos t\right)\, dt=4\sqrt{2}b\pi R^2$$ El valor medio de la densidad a lo largo de $C_a$ es $$f_m=2R^2$$ es decir, la misma para todas las curvas $C_a$. Si dibujamos los aros con una pequeña anchura y los coloreamos según el valor de la densidad lineal, obtendremos
Gráfica

Índice de tema