Enunciado
Sea $A$ el área de la porción de cilindro $x^2+y^2=9$ que pertenece al primer octante y está comprendida entre los planos $y=x$, $y=\sqrt{3}x$ y $z=x$. Representa esa superficie y calcula $A$ haciendo uso de integrales sobre curvas.
Paso 1
Al ser la superficie una porción de un cilindro vertical, la proyección en el plano $XY$ es un arco de curva. Por esta razón podemos utilizar integrales de línea, en particular sobre una curva plana, para calcular ese área de superficie: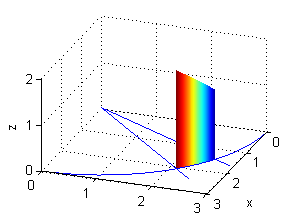
Esta es una de las interpretaciones de la integral de línea de un campo escalar. Hemos de determinar entonces
- cuál es la curva $C$ (proyección en $XY$ de la superficie)
- cuál es el campo escalar que se ha de integrar (altura en cada punto de la proyección)
Ver
Por ser parte de un cilindro circular, la superficie se proyectará en un arco de circunferencia. Para saber cuál es ese arco, hemos de utilizar los planos $y=x$ e $y=\sqrt{3}x$, o mejor, sus proyecciones en el plano $XY$; así sabemos que $C$ es el arco de $x^2+y^2=9$ entre las rectas $y=x$ e $y=\sqrt{3}x$.
El campo escalar que hemos de integrar es el que valga la altura en cada punto $(x,y)$ de esa curva proyección, luego será $$f(x,y)=x$$ La integral de línea que se ha de calcular es $$\mbox{área}=\int_C x\, ds$$
Paso 2
Parametrizamos la curva y calculamos el elemento diferencial de arco. Hazlo tú y pulsa en 'Ver'. Necesitarás saber calcular el elemento diferencial de arco en paramétricas.
Ver
$$x=3\cos t \ ,\ \ y=3\,\mbox{sen}\, t \ \ \Rightarrow\ \ ds=3\, dt$$
Paso 3
Hallamos la variación del parámetro $t$ para que las coordenadas anteriores dibujen el arco $C$:
$t\in[0,\pi/2]$
$t\in[0,\pi/3]$
$t\in[\pi/4,\pi/3]$
Eso no es correcto, así tomaríamos todo el primer cuadrante de circunferencia.
Eso no es correcto, así tomaríamos un arco demasiado grande.
En efecto, $\frac{\pi}{4}$ es el ángulo correspondiente a $y=x$ con $x$ positivo y
$\frac{\pi}{3}$ el correspondiente a $y=\sqrt{3}x$ también con $x$ positivo:
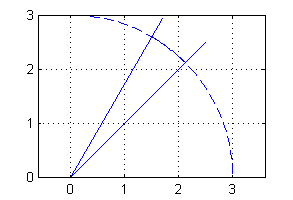

Paso 4
Calculamos la integral $$\mbox{área}=\int_C x\, ds$$ hazlo tú y pulsa en 'Ver'
Ver
$$\mbox{área}=\int_C x\, ds= 9\int_{\pi/4}^{\pi/3} \cos t\, dt=\frac{9}{2}(\sqrt{3}-\sqrt{2})$$
Resumen
- identificar los elementos del problema: curva proyección y función altura
- parametrizar la curva
- hallar los extremos de integración
- calcular la integral.