Enunciado
Encuentra la longitud de la curva cerrada dada por la ecuación $\rho(\theta)=\mbox{sen}^3\frac{\theta}{3}$. Dibújala utilizando el ordenador.
Paso 1
Para calcular la longitud de una curva debemos determinar su elemento diferencial de arco, $ds$. En este caso, puesto que $\frac{d\rho}{d\theta}=\mbox{sen}^2\frac{\theta}{3}\cos\frac{\theta}{3}$, ese elemento diferencial es
$ds=\sqrt{1+(\mbox{sen}^2\frac{\theta}{3}\cos\frac{\theta}{3})^2}\, d\theta$
$ds=\sqrt{\mbox{sen}^6\frac{\theta}{3}+(\mbox{sen}^2\frac{\theta}{3}\cos\frac{\theta}{3})^2}\, d\theta$
¡No! Para una curva expresada en polares, el elemento $ds$ no se obtiene así.
En efecto, así se calcula el elemento diferencial de arco en polares pero esta expresión puede simplificarse un poco sacando $\mbox{sen}^4\frac{\theta}{3}$ factor común a los dos sumandos. Hazlo tú y pulsa en Continuar.
Ya tenemos que
$$ds=\mbox{sen}^2\frac{\theta}{3}\ d\theta$$
Paso 2
Debemos encontrar ahora cuáles son los extremos de integración. Para que los puntos, en coordenadas polares $[\mbox{sen}^3\frac{\theta}{3},\theta]$ dibujen el arco una sóla vez, los valores de $\theta$ deben variar en
$\left[0,\frac{2\pi}{3}\right]$, ya que la curva tiene tres lazos para $[0,2\pi]$
$[0,2\pi]$, ya que es así muchas veces
$[0,6\pi]$, ya que por ser $\mbox{sen}\,\theta$ $2\pi-$periódica, $\mbox{sen}\,\frac{\theta}{3}$ es $6\pi-$periódica
$[0,3\pi]$, pues los valores de $\mbox{sen}^3\frac{\theta}{3}$ obtenidos con $\theta\in[0,3\pi]$ y con $\theta\in[3\pi,6\pi]$ son opuestos, proporcionando el mismo punto del plano
Eso no es cierto.
Aquí no es así, pues dentro del seno, el ángulo está dividido por 3, y eso cambia el periodo.
Es cierto que el periodo de $\mbox{sen}\,\frac{\theta}{3}$ es $6\pi$, pero debes tener en cuenta que $\mbox{sen}\,\frac{\theta}{3}=-\mbox{sen}\,\left(\frac{\theta}{3}+\pi\right)$
En efecto, ya que el punto de coodenadas $[\rho,\theta]$ es el mismo que el coordenadas $[-\rho,\theta+\pi]$, o también $[-\rho,\theta+3\pi]$, lo que significa que los valores de $\mbox{sen}^3\frac{\theta}{3}$ para $\theta\in[0,3\pi]$ y para $\theta\in[3\pi,6\pi]$ proporcionan el mismo punto del plano: para $\theta\in[3\pi,6\pi]$ la curva repite los mismos puntos que ya se habían dibujado para
$\theta\in[0,3\pi]$.
Por tanto, la longitud de la curva viene dada por la integral
$$\mbox{longitud}=\int_0^{3\pi} \mbox{sen}^2 \frac{\theta}{3}\, d\theta$$
Paso 3
Por último, calculamos esa integral. Hazlo tú y pulsa en 'Ver'.
Ver
$$\mbox{longitud}=\frac{1}{2}\int_0^{3\pi} \left (1-\cos\frac{2\theta}{3}\right) \, d\theta=\frac{1}{2}\left [\theta-\frac{3}{2}\mbox{sen}\frac{2\theta}{3}\right]_0^{3\pi}=\frac{3\pi}{2}$$
Para dibujarla en el ordenador podemos poner
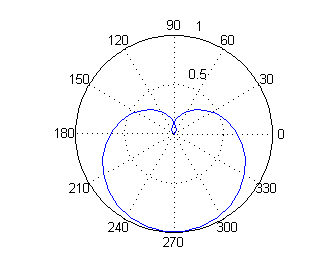
o bien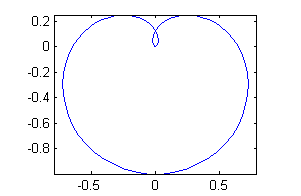
t=linspace(0,3*pi,50); polar(t,(sin(t/3)).^3)

o bien
t=linspace(0,3*pi); plot(cos(t).*(sin(t/3)).^3,sin(t).*(sin(t/3)).^3) axis equal

Resumen
- encontrar el elemento diferencial de arco,
- determinar los extremos de integración,
- calcular la integral y dibujar la curva.