Índice de tema

 

Enunciado

Los hipotrocoides son las curvas de ecuaciones paramétricas $$C_{a,b}: \hspace{.3cm} x(t)=a\cos t+b\cos \frac{at}{2} \hspace{.2cm} , \hspace{.2cm} y(t)=a\, \mbox{sen}\, t+b\, \mbox{sen}\frac{at}{2} \hspace{.2cm} , \hspace{.3cm} t\in[0,2\pi]$$
  1. Encuentra a mano su elemento diferencial de arco.
  2. Prepara una función para el ordenador, con variables de entrada los coeficientes $a$ y $b$ y como salida el valor de la longitud de $C_{a,b}$; la función debe también dibujar la curva $C_{a,b}$.
  3. Prueba la función que has preparado con los pares de valores
    1. $a=8$, $b=4$
    2. $a=8$, $b=10$
    3. $a=-8$, $b=10$
    y compara las longitudes obtenidas.

Resolución del primer apartado

Hallemos el elemento diferencial de arco para estas curvas expresadas mediante paramétricas. Hazlo tú y pulsa en 'Ver'.
Ver
$${\bf r}(t)=\left(a\cos t+b\cos \frac{at}{2}, a\, \mbox{sen} t+b\, \mbox{sen}\,\frac{at}{2}\right) \hspace{.3cm} \Rightarrow \hspace{.3cm} {\bf r'}(t)=\left(-a\, \mbox{sen}\, t-\frac{ab}{2}\, \mbox{sen} \frac{at}{2}, a\cos t-\frac{ab}{2}\cos\frac{at}{2}\right)$$ luego $$ds=|{\bf r'}(t)|\ dt= \,|a|\sqrt{1+\frac{b^2}{4}-b\cos\left(\left(1+\frac{a}{2}\right)t\right)}\, dt$$

Resolución del segundo apartado

Antes de escribir la función para el ordenador debemos saber cómo se calcula la longitud de una curva. Si ya lo tenemos claro pasamos a preparar la función, llamada hipotrocoide, con dos variables de entrada, $a$ y $b$, y una de salida que será la longitud. La función dibujará la curva correspondiente. Seguiremos los pasos que se presentan a continuación. En cada uno, pulsa en 'Continuar' cuando lo hayas completado.
  • Declara la función con sus dos variables de entrada y su variable de salida
function longitud=hipotrocoides(a,b)
  • genera un vector,'t', de valores del parámetro t
t=0:pi/50:2*pi;
  • dibuja la curva y fija igual escala en los dos ejes
plot(a*cos(t)+b*cos(a*t/2),a*sin(t)-b*sin(a*t/2))
axis equal
  • declara una variable simbólica y calcula la integral de línea; cierra la función
syms u
longitud=abs(a)*double(int(sqrt(1+b^2/4-b*cos((1+a/2)*u)),u,0,2*pi));
end
Para preparar esta función hemos utilizado la expresión del elemento diferencial de arco calculado en el primer apartado. Otra opción es calcular ese elemento diferencial dentro de la función. Repetimos el proceso ahora con ese supuesto, llamando hipotrocoide2 a la nueva función:
  • Declara la función con sus dos variables de entrada y su variable de salida
function longitud=hipotrocoides2(a,b)
  • declara una variable simbólica y genera un vector simbólico con las componentes de la curva escritas para esa variable
syms u
r=[a*cos(u)+b*cos(a*u/2) a*sin(u)-b*sin(a*u/2)];
  • Halla la derivada de este vector y la longitud de la curva integrando su módulo (respecto de u)
dr=diff(r);
longitud=double(int(sqrt(dr(1)^2+dr(2)^2),u,0,2*pi));
  • genera un vector t de parámetros y los vectores x e y sustituyendo en las componentes de r, la variable u por el vector t
t=0:pi/50:2*pi;
x=subs(r(1),u,t);
y=subs(r(2),u,t);
  • dibuja la curva de componentes (x,y) y fija igual escala en los ejes; cierra la función 
plot(x,y)
axis equal
end

Resolución del tercer apartado

  • Ejecutando 
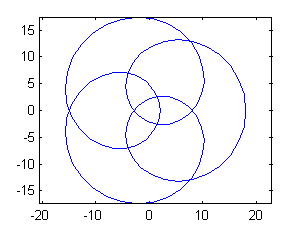
    hipotrocoides(8,4)
    obtenemos que $\mbox{longitud}(C_{8,4})= 106.9191$ y $C_{8,4}$ es la curva
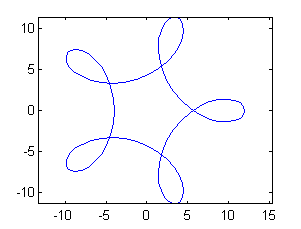
    Gráfica
  • Ejecutando 
    hipotrocoides(8,10)
    obtenemos que $\mbox{longitud}(C_{8,10})= 253.8470$ y $C_{8,10}$ es la curva
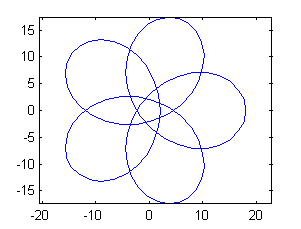
    Gráfica
  • Ejecutando 
    hipotrocoides(-8,10)
    obtenemos que $\mbox{longitud}(C_{-8,10})= 253.8470$ y $C_{-8,10}$ es la curva
    Gráfica