Definición (Gradiente).- Es el campo vectorial $${\kern 1pt} {\mathop{\rm grad}\nolimits} {\kern 1pt} (f(x,y,z)) = \nabla f(x,y,z) = {{\partial f} \over {\partial x}}(x,y,z){\kern 1pt} {\bf{i}} + {{\partial f} \over {\partial y}}(x,y,z){\kern 1pt} {\bf{j}} + {{\partial f} \over {\partial z}}(x,y,z){\kern 1pt} {\bf{k}}$$
IMPORTANTE RECORDAR:
- La relación entre la derivada direccional y el campo gradiente de un campo escalar diferenciable $f$ es: ${D_{\bf{u}}}f = \nabla f \cdot {\bf{u}}$ , siendo ${\bf{u}}$ un vector unitario.
- La derivada direccional "mide el cambio de $f$ en la dirección de ${\bf{u}}$.
- La derivada direccional es máxima en la dirección del gradiente.
Definición (Campo vectorial conservativo y función potencial).- ${\bf{F}}$ es un campo vectorial conservativo si existe un campo escalar $f$, diferenciable, de forma que $${\bf{F}} = \nabla f$$
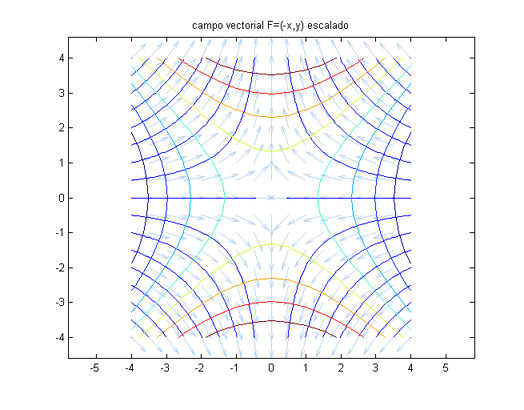
Definición (Líneas equipotenciales).- Sea ${\bf{F}} = \nabla f(x,y)$, siendo $f(x,y)$ diferenciable. Las líneas equipotenciales de ${\bf{F}}$ son las curvas que verifican $$f(x,y) = C$$
Definición (Superficies equipotenciales).- Sea ${\bf{F}} = \nabla f(x,y,z)$, siendo $f(x,y,z)$ diferenciable. Las superficies equipotenciales de ${\bf{F}}$ son las superficies que verifican $$f(x,y,z) = C$$
PROPIEDAD: Las líneas equipotenciales y las superficies equipotenciales son perpendiculares a las líneas de fuerza.
Definición (Divergencia).- Dado el campo vectorial $${\bf{F}}(x,y,z) = M(x,y,z){\bf{i}} + N(x,y,z){\bf{j}} + P(x,y,z){\bf{k}}$$ se define su divergencia como el campo escalar $${\mathop{\rm div}\nolimits} {\bf{F}} = {{\partial M} \over {\partial x}} + {{\partial N} \over {\partial y}} + {{\partial P} \over {\partial z}}$$ siempre que existan esas derivadas parciales de M, N y P.
Definición (Rotacional).- Dado el campo vectorial $${\bf{F}}(x,y,z) = M(x,y,z){\bf{i}} + N(x,y,z){\bf{j}} + P(x,y,z){\bf{k}}$$ se define su rotacional como el campo vectorial $${\mathop{\rm rot}\nolimits} {\bf{F}} = \left( {{{\partial P} \over {\partial y}} - {{\partial N} \over {\partial z}}} \right){\bf{i}} + \left( {{{\partial M} \over {\partial z}} - {{\partial P} \over {\partial x}}} \right){\bf{j}} + \left( {{{\partial N} \over {\partial x}} - {{\partial M} \over {\partial y}}} \right){\bf{k}}$$ siempre que existan esas derivadas parciales de M, N y P.
Definición (Laplaciano).- Es el campo escalar $$\Delta f(x,y,z) = {\kern 1pt} {\mathop{\rm div}\nolimits} {\kern 1pt} (\nabla f(x,y,z)) = {{{\partial ^2}f} \over {\partial {x^2}}}(x,y,z) + {{{\partial ^2}f} \over {\partial {y^2}}}(x,y,z) + {{{\partial ^2}f} \over {\partial {z^2}}}(x,y,z)$$ El laplaciano de $f$ también se denota por ${\nabla ^2}f$.
Ejercicios interactivos:
