Ejercicios preliminares e instantáneos. Campos escalares y vectoriales

1. Recuerda que $(x_1,y_1,z_1)\cdot(x_2,y_2,z_2)=x_1x_2+y_1y_2+z_1z_2$
2. El producto escalar de dos vectores puede utilizarse para hallar la proyección de uno de ellos sobre el otro. Así, la proyección de ${\bf u}$ sobre ${\bf v}$ es el vector $$\frac{{\bf u}\cdot{\bf v}}{|{\bf v}|^2}{\bf v}$$

Ver solución

1. 1. $(2,7,-4)\cdot (1,0,-2)=10$
   2. $(1,-2,a)\cdot (2,-1,a)=4+a^2$
   3. $(0,1-a,1)\cdot (2,a^2,a)=-a^3+a^2+a$
   
   El código para el ordenador sería:

   	sum([2,7,-4].*[1,0,-2])
   	syms a
   	sum([1,-2,a].*[2,-1,a])
   	sum([0,1-a,1].*[2,a^2,a])
   	

   o bien

   	dot([2,7,-4],[1,0,-2])
   	syms a
   	dot([1,-2,a],[2,-1,a])
   	dot([0,1-a,1],[2,a^2,a])
   	

2. La proyección de ${\bf u}=(2,7,-4)$ sobre ${\bf v}=(1,0,-2)$ es el vector $$\frac{{\bf u}\cdot{\bf v}}{|{\bf v}|^2}{\bf v}=\frac{10}{5}(1,0,-2)=(2,0,-4)$$ En la figura puedes ver los vectores del primer apartado junto con la proyección del primero sobre el segundo:
   

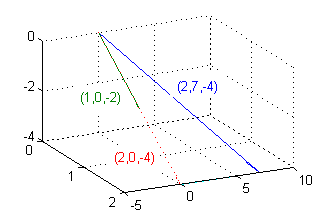
   	quiver3(0,0,0,2,7,-4,1) % vector (2,7,-4) colocado en el punto (0,0,0)
   	hold on
   	quiver3(0,0,0,1,0,-2,1) % vector (1,0,-2) colocado en el punto (0,0,0)
   	quiver3(0,0,0,2,0,-4,1) % proyección de (2,7,-4) sobre (1,0,-2)
   	plot3([2 2],[7 0],[-4 -4],'c')
   	hold off
   	view([64,30])
   	

Recuerda que $$(x_1,y_1,z_1)\times(x_2,y_2,z_2)=\left|\begin{array}{lll} {\bf i} & {\bf j} & {\bf k}\\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{array}\right|$$ Ver solución

1. $(2,7,-4)\times (1,0,-2)=-7(2,0,1)$
2. $(1,-2,a)\times (2,-1,a)=(-a,a,3)$
3. $(0,1-a,1)\times (2,a^2,a)=(a(1-2a),2,2(a-1))$

El código para estos productos vectoriales es

		cross([2,7,-4],[1,0,-2])
		syms a
		cross([1,-2,a],[2,-1,a])
		cross([0,1-a,1],[2,a^2,a])

Recuerda que el vector producto vectorial de dos vectores es perpendicular a ambos y su sentido se rige por la regla de la mano derecha o del sacacorchos:

	quiver3(0,0,0,2,7,-4,1) % vector (2,7,-4) colocado en el punto (0,0,0)
	hold on
	quiver3(0,0,0,1,0,-2,1) % vector (1,0,-2) colocado en el punto (0,0,0)
	quiver3(0,0,0,-14,0,-7,1) % vector (2,7,-4)x(1,0,-2) en el punto (0,0,0)
	hold off
	view([64,30])
	

1. es errónea, debería ser ${\bf F}(x,y,z)$;
2. tiene sentido;
3. habría que escribir ${\bf F}(x,y,z)=(1,\mbox{sen} (xz) , -xy^2z)$ o bien ${\bf F}(x,y,z)={\bf i}+\mbox{sen} (xz) \, {\bf j}+ -xy^2z \, {\bf k}$;
4. eso no tiene arreglo;
5. la parte de la izquierda indica una función escalar, mientras que la derecha es un vector;
6. tiene sentido tal como está.

Un campo escalar asocia a cada punto un número (un sólo dato, por tanto), mientras que un campo vectorial asocia a cada punto tres datos: un número, una dirección y un sentido.
Ver solución

1. campo escalar de dimensión 2;
2. campo escalar de dimensión 3;
3. campo vectorial de dimensión 3;
4. campo vectorial de dimensión 3;
5. campo vectorial de dimensión 3;
6. campo vectorial de dimensión 3;
7. campo vectorial de dimensión 3;
8. campo escalar de dimensión 3;
9. campo escalar de dimensión 2.

Verdadero, esa es la definición de continuidad para campos vectoriales.

Recuerda que una función real de una variable real es de clase $C^r$ si admite derivada de orden $r$ y ésta es una función continua.
Ver solución

$M(x,y,z)=2xy$ es de clase $C^r$ en todo el espacio para cualquier $r$, $N(x,y,z)=-\sqrt{x}$ es de clase $C^r$ en el semiespacio $x>0$ y $P(x,y,z)=\frac{1}{z-1}$ es de clase $C^r$ en $z\neq 1$.

1. Todas las componentes son continuas y derivables hasta cualquier orden;
2. para tener cualquier orden de derivación debemos restringir el dominio a $x>0$;
3. las componentes son continuas, para ser derivables deberíamos tomar $z\neq 0$ y $y\neq 2$.

Recuerda que $\nabla f(x,y,z)=(f'_x,f'_y,f'_z)$
Ver solución

• $\nabla f(x,y,z)=(1,z,y)$. Para calcularlo en el ordenador pondríamos

  		syms x y z
  		f=x+y*z;
  		[diff(f,x),diff(f,y),diff(f,z)]
  		

  El cálculo de una muestra de vectores de este campo gradiente y su trazado se haría con

  		[X,Y,Z]=meshgrid(-1:1); % malla de puntos donde se dibujarán los vectores
  		F=X+Y.*Z; % definición del campo escalar
  		[M,N,P]=gradient(F); % cálculo del gradiente en los puntos de la malla
  		quiver3(X,Y,Z,M,N,P) % trazado de los vectores
  		

  En la figura puedes ver una muestra de este gradiente desde dos puntos de vista diferentes:
  
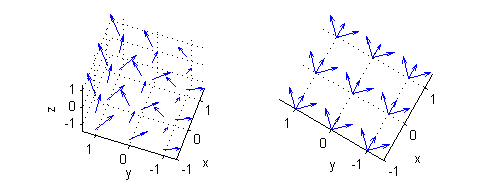
• $\nabla g(x,y,z)=\cos(xy^2z^3)(y^2z^3,2xyz^3,3xy^2z^2)$

Recuerda que si ${\bf F}=M{\bf i}+N \, {\bf j} +P \, {\bf k}$, entonces $$\mbox{div} {\bf F}=M'_x+N'_y+P'_z$$ y $${\bf rot F}=\left|\begin{array}{lll} {\bf i} & {\bf j} & {\bf k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ M & N & P \end{array}\right|$$ Ver solución

• $$\mbox{div} {\bf F}=-xy^2$$ $${\bf rot F}=(-2xyz-x\cos(xz),y^2z,z\cos(xz))$$ Para calcularlos simbólicamente en el ordenador pondríamos

    		 syms x y z
    		 M=1; N=sin(x*z); P=-x*y^2*z;
    		 div=diff(M,x)+diff(N,y)+diff(P,z)
    		 rot=[diff(P,y)-diff(N,z),diff(M,z)-diff(P,x),diff(N,x)-diff(M,y)]
    		 

  Numéricamente, en una muestra de puntos, esta divergencia y este rotacional se calculararían así:

    		 [X,Y,Z]=meshgrid(-1:1);
    		 M=ones(size(X)); N=sin(X.*Z); P=-X.*Y.^2.*Z;
    		 div=divergence(X,Y,Z,M,N,P)
    		 [rotx,roty,rotz]=curl(X,Y,Z,M,N,P)
  

• $$\mbox{div} {\bf G}=ze^{yz}+3x$$ $${\bf rot G}=(-ye^{yz},-3z,1)$$
• $$\mbox{div} {\bf H}=-\mbox{sen} x+e^{xz}+xy$$ $${\bf rot H}=(xz-xye^{xz},-yz,yze^{xz})$$

Todos los campos escalares suficientemente derivables deben cumplir que el rotacional de su gradiente sea nulo. Igualmente es nula la divergencia de un campo vectorial rotacional.