Enunciado
- Sean $a$ y $b$ números reales. Consideramos las funciones
$$h(t)=U(t)e^{-at}\mbox{sen}\, bt \hspace{.4cm}, \hspace{.4cm} g(t)=\int_0^t e^{-ax}\mbox{sen}\, bx\, dx \hspace{.4cm}, \hspace{.4cm} f(t)=t\int_0^t e^{-ax}\mbox{sen}\, bx\, dx$$
Halla la transformada de Laplace de la función $f(t)$, indicando su dominio de definición.
- Toma valores concretos para los parámetros $a$ y $b$ y representa las correspondientes funciones $h$, $g$ y $f$ del apartado anterior, junto con sus transformadas de Laplace. Dispón las seis funciones en una matriz de gráficas de dimensión 2x3.
Resolución del primer apartado
Paso 1
Nos conviene ver la función $f(t)$ como el producto $$f(t)=tg(t)$$ y a su vez la función $g(t)$ como la integral $$g(t)=\int_0^t h(x)\, dx$$ Empezaremos por tanto encontrando la transformada de $h(t)$; las de $g(t)$ y $f(t)$ se obtendrán mediante propiedades a partir de ella. Así pues el primer paso es hallar $$H(s)={\cal L}[h(t)]={\cal L}[U(t)e^{-at}\mbox{sen}\, bt]$$ El factor $e^{-at}$ presente en $h(t)$ debe hacernos pensar en la propiedad de traslación en la variable $s$; teniendo en cuenta cuál es la transformada de la función $\mbox{sen}\, bt$, (ver tabla básica)
$$H(s)={\cal L}[U(t)e^{-at}\mbox{sen}\, bt]=\frac{a}{(s+a)^2+a^2} \hspace{.4cm}, \hspace{.4cm} s>a$$
$$H(s)={\cal L}[U(t)e^{-at}\mbox{sen}\, bt]=\frac{b}{(s-a)^2+b^2} \hspace{.4cm}, \hspace{.4cm} s>a$$
Ninguna es correcta
$$H(s)={\cal L}[U(t)e^{-at}\mbox{sen}\, bt]=\frac{b}{(s+a)^2+b^2} \hspace{.4cm}, \hspace{.4cm} s>-a$$
Revisa la transformada del $\mbox{sen}\, bt$ y el uso de la propiedad.
Revisa el signo del factor de traslación.
Sí hay una correcta
En efecto, ésa es la expresión correcta, pues se está evaluando la función
${\cal L}[U(t)\mbox{sen}\, bt](s)=\frac{b}{s^2+b^2}$ en $s+a$; al estar ${\cal L}[U(t)\mbox{sen}\, bt](s)$ definida en $s>0$, la transformada de $U(t)e^{-at}\mbox{sen}\, bt$ lo estará en $s>-a$.
Paso 2
Hallar la transformada de $g(t)=\int_0^t h(x)\, dx$ a partir de la de $h(t)$. Para ello utilizaremos la propiedad de la transformada de la integral. Hazlo tú y pulsa en 'Ver'.
Ver
Únicamente debemos dividir por $s$ la transformada de $h(t)$:
$${\cal L}[g(t)]=\frac{b}{s[(s+a)^2+b^2]} \hspace{.4cm}, \hspace{.4cm} s>-a$$
Paso 3
Encontrar la transformada de $f(t)=tg(t)$. Esto es sencillo, porque ...
Conocemos las transformadas de $t$ y de $g(t)$ y bastará hacer su producto.
Conocemos las transformadas de $t$ y de $g(t)$ y bastará hacer su convolución.
Podemos utilizar la propiedad de la derivada de la transformada
¡La transformada del producto NO es el producto de las transformadas!
¡La transformada del producto NO es la convolución de las transformadas!
Esa es la propiedad adecuada, pues la derivada de la transformada de $g(t)$ coincide con el opuesto de la transformada de $t$ por la función $g(t)$; en este caso
$${\cal L}[f(t)]={\cal L}[tg(t)]=-\frac{d}{ds}\left(\frac{b}{s[(s+a)^2+b^2]}\right)=
\frac{3s^2+4as+a^2+b^2}{s[(s+a)^2+b^2]} \hspace{.4cm}, \hspace{.4cm} s>-a$$
Resolución del segundo apartado
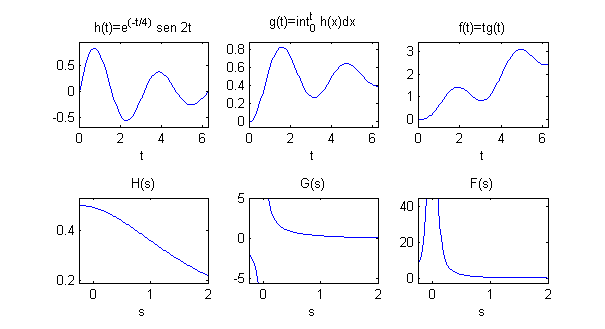
Tomaremos $a=1/4$ y $b=2$. Para representar estas seis funciones en una matriz de gráficos recurrimos al comando 'subplot'; recuerda que dentro de una matriz de gráficos generada con 'subplot(n,m,k)', los gráficos se van numerando por filas, por ejemplo el gráfico de la segunda fila, primera columna será el correspondiente a k=m+1. Intenta elaborar un fichero que dibuje estas seis gráficas y pulsa en 'Ver'
Ver
En un fichero escribimos
clear var % borramos variables definidas con anterioridad
syms t s; % declaramos t y s como simbólicas
h=exp(-t/4)*sin(2*t)*heaviside(t); % función h
g=int(h,0,t)*heaviside(t); % función g
f=t*g; % función f
subplot(2,3,1) % nos situamos en la primera fila, primera columna
ezplot(h) % representación de h
title('h(t)=e^{(-t/4)} sen 2t')
subplot(2,3,4) % nos situamos en la segunda fila, primera columna
ezplot(laplace(h),[-1/4,2]) % representación de H
title('H(s)')
subplot(2,3,2) % nos situamos en la primera fila, segunda columna
ezplot(g) % representación de g
title('g(t)=int_0^t h(x)dx')
subplot(2,3,5) % nos situamos en la segunda fila, segunda columna
ezplot(laplace(g),[-1/4,2]) % representación de G
title('G(s)')
subplot(2,3,3) % nos situamos en la primera fila, tercera columna
ezplot(f) % representación de f
title('f(t)=tg(t)')
subplot(2,3,6) % nos situamos en la segunda fila, tercera columna
ezplot(laplace(f),[-1/4,2]) % representación de F
title('F(s)')
De su ejecución resultará la figura