Índice de tema

 

Enunciado

  1. Utiliza transformadas de Laplace para hallar la solución del siguiente problema de valor inicial $$y''(t)+9y(t)=f(t)\ \ , \ \ y(0)=0\ , \ \ y'(0)=1$$ siendo $f(t)$ la función que vale $\mbox{sen}\, 3t$ para $t\in[0,2\pi]$ y cero si no.
  2. Comprueba el resultado con el ordenador.
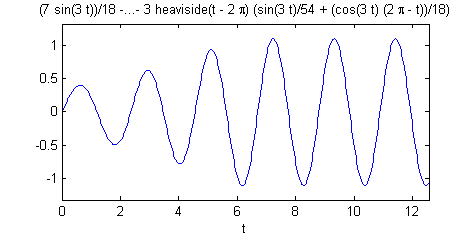
  3. Representa la función $y(t)$ para $t\in[0,4\pi]$.

Resolución del primer apartado

Paso 1

Escribir el segundo término de la ecuación, $f(t)$, con una sóla expresión, para hacer su transformada a partir de otras conocidas. Este paso podemos obviarlo si encontramos la transformada de $f(t)$ mediante la definición, pero el cálculo de la integral es más laborioso que escribir $f(t)$ como una sola expresión:
$$f(t)= U(t-2\pi)\,\mbox{sen}\, 3t$$
$$f(t)=[U(t+2\pi)-U(t-2\pi)]\mbox{sen}\, 3t $$
$$f(t)=[U(t+2\pi)-U(t)]\mbox{sen}\, 3t $$
Ninguna es correcta
$$f(t)=[U(t)-U(t-2\pi)]\mbox{sen}\, 3t $$
Esa función vale cero hasta $t=2\pi$.
Esa función vale $\mbox{sen}\, 3t$ entre $t=-2\pi$ y $t=2\pi$ y cero en el resto.
Esa función vale $\mbox{sen}\, 3t$ entre $t=-2\pi$ y $t=0$ y vale cero en el resto.
Sí hay una correcta
En efecto, ésa es la expresión correcta.

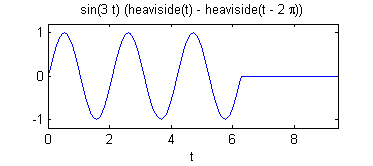
Gráfica

Paso 2

Transformar la función $f(t)=[U(t)-U(t-2\pi)]\mbox{sen}\, 3t $, haciendo uso de la propiedad de traslación en la variable $t$ puesto que debido a la periodicidad de la función seno, $$U(t-2\pi)\mbox{sen}\, 3t=U(t-2\pi)\mbox{sen}\, (3(t-2\pi))$$
$${\cal L}[f(t)]=\frac{1-e^{-2\pi s}}{s^2+9}$$
$${\cal L}[f(t)]=\frac{3(1-e^{2\pi s})}{s^2+9}$$
$${\cal L}[f(t)]=\frac{3(1-e^{-2\pi t})}{s^2+9}$$
$${\cal L}[f(t)]=\frac{3(1-e^{-2\pi s})}{s^2+9}$$
Cuidado con la transformada del seno.
Cuidado con el signo del factor de desplazamiento
Cuidado con el nombre de las variables.
En efecto, esa es la transformada buscada.

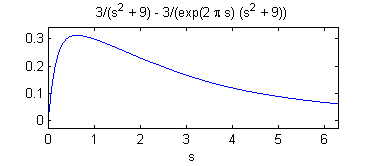
Gráfica

Paso 3

Transformar la ecuación diferencial en una ecuación algebraica en la variable $Y(s)={\cal L}[y]$. Para ello utilizaremos la linealidad de la transformada y la propiedad de la transformada de la derivada. Hazlo tú y pulsa en 'Ver' cuando lo tengas.
Ver
Al tomar transformadas a ambos lados de la ecuación se obtiene, $$(s^2+9)Y(s)-1=F(s) \hspace{.4cm} \Rightarrow \hspace{.4cm} Y(s)=3\frac{1-e^{-2\pi s}}{(s^2+9)^2}+\frac{1}{s^2+9}$$

Paso 4

Hallar la función $y(t)={\cal L}^{-1}[Y(s)]$. Por una parte, utilizando la tabla básica de transformadas, $$\frac{1}{s^2+9}=\frac{1}{3}{\cal L}[\mbox{sen}\, 3t]$$ Para hallar la transformada inversa de $\frac{1-e^{-2\pi s}}{(s^2+9)^2}$, observamos que el factor $e^{-2\pi s}$ nos permitirá aplicar la traslación en la variable $t$, así que únicamente hemos de determinar la inversa de $\frac{1}{(s^2+9)^2}$. Para ello, aplicamos que $$\frac{1}{(s^2+9)^2}=\frac{1}{s^2+9}\frac{1}{s^2+9}$$ luego
$${\cal L}^{-1}[\frac{1}{(s^2+9)^2}]={\cal L}^{-1}[\frac{1}{s^2+9}]{\cal L}^{-1}[\frac{1}{s^2+9}]=\frac{1}{9}\mbox{sen}^2\, 3t$$
La propuesta no es correcta.
¡Cuidado! La transformada de Laplace de dos funciones no es el producto de las transformadas, ni la inversa del producto es el producto de las inversas.
En efecto, debemos recurrir a la convolución, pues la transformada de la convolución es el producto de las transformadas, así que $${\cal L}^{-1}[\frac{1}{(s^2+9)^2}]={\cal L}^{-1}[\frac{1}{s^2+9}]*{\cal L}^{-1}[\frac{1}{s^2+9}]= \frac{1}{9} \mbox{sen}\, 3t *\mbox{sen}\, 3t$$ Realiza esta convolución, utilizando para la integral que $$\mbox{sen}\, a \ \mbox{sen}\, b=\frac{1}{2}[\cos(a-b)-\cos(a+b)]$$ Pulsa en 'Continuar' cuando la hayas calculado.
$$\mbox{sen}\, 3t *\mbox{sen}\, 3t=\int_0^t \mbox{sen}\, 3(t-x) \mbox{sen}\, 3x \, dx= \frac{1}{2}\int_0^t(\cos(3t-6x)-\cos 3t)\, dx$$ y esta última integral es
$\frac{1}{2}\int_0^t(\cos(3t-6x)-\cos 3t)\, dx=\frac{1}{2}\left[\frac{1}{3}\mbox{sen}\,3t-\frac{1}{3}\mbox{sen}\, 3t\right]$
Ninguna de las opciones es correcta.
$\frac{1}{2}\int_0^t(\cos(3t-6x)-\cos 3t)\, dx=\frac{1}{2}\left[\frac{1}{3}\mbox{sen}\,3t-t\cos 3t\right]$
¡Cuidado! La variable de integración es la $x$, no la $t$.
Sí hay una correcta.
Esa es la convolución, luego $${\cal L}^{-1}[\frac{1}{(s^2+9)^2}]=\frac{1}{9} \mbox{sen}\, 3t *\mbox{sen}\, 3t=\frac{1}{18}\left[\frac{1}{3}\mbox{sen}\,3t-t\cos 3t\right]=g(t)$$ Por tanto, la transformada inversa de la función $Y(s)=3\frac{1-e^{-2\pi s}}{(s^2+9)^2}+\frac{1}{s^2+9}$ será $$y(t)=3g(t)-3g(t-2\pi)U(t-2\pi)+\frac{1}{3}\mbox{sen}\, 3t$$ o bien $$y(t)=\frac{1}{6}\left(\frac{7}{3}\mbox{sen}\, 3t-t\cos 3t\right)-\frac{1}{6}\left( \frac{1}{3}\mbox{sen}\, 3t-(t-2\pi)\cos 3t\right)U(t-2\pi)$$ que también puede escribirse como $$y(t)=\left\{\begin{array}{lll} \frac{1}{6}\left(\frac{7}{3}\mbox{sen}\, 3t-t\cos 3t\right) & ,& 0 \leq t \leq 2\pi \\ \frac{1}{6}\left(2\,\mbox{sen}\, 3t-2\pi\cos 3t\right) & ,& t\geq 2\pi \end{array}\right.$$

Resolución del segundo apartado

Podemos comprobar el cálculo de la inversa y cómo esa función es efectivamente solución de la ecuación, siguiendo los siguientes pasos:
  1. declarar 's' como variable simbólica
  2. guardar en 'y' la inversa de $Y(s)$
  3. comprobar que $y''+9y$ es la función $f$ (para hacer esta comprobación necesitarás simplificar, con 'simplify', el resultado de $y''+9y$
Escribe en un fichero las líneas con las que se llevan a cabo estos cálculos y pulsa en 'Ver'.
Ver
En un fichero escribimos 
syms s
y=ilaplace(3*(1-exp(-2*pi*s))/((9+s^2)^2)+1/(9+s^2));
g=diff(y,2)+9*y;
simplify(g)
Su ejecución resultará 
-sin(3*t)*(heaviside(t - 2*pi) - 1)
como queríamos comprobar.

Resolución del tercer apartado

Para representar la solución en $[0,4\pi]$ basta añadir al fichero anterior la línea 
ezplot(y,[0,4*pi])  %%%% representación de la solución
La figura que resulta es

Gráfica