Enunciado
Encuentra $f(t)$ tal que $f(0)=2$ satisfaciendo además que $$f'(t)+4\int_0^t f(x)\, dx=t-\mbox{sen}\, t$$
- Utilizando transformadas de Laplace
- Convirtiéndola en una ecuación de segundo orden y resolviéndola con técnicas de ecuaciones diferenciales lineales.
Representa después en una misma figura las funciones $f(t)$, $t-\mbox{sen}\, t$, $f'(t)$ y $4\int_0^t f(x)\, dx$ para $t\in[0,4\pi]$.
Resolución utilizando tansformadas de Laplace
Paso 1
Tomar transformadas a toda la ecuación: para ello necesitamos, además de la propiedad de linealidad, las propiedades de transformada de la derivada y de la transformada de la integral. Para transformar el segundo término basta con la tabla básica de transformadas. Encuentra la ecuación que verifica la función $F(s)={\cal L}[f(t)]$ y pulsa en 'Ver'.
Ver
Puesto que $${\cal L}[f'(t)]=sF(s)-f(0) \hspace{.5cm} \mbox{y} \hspace{.5cm} {\cal L}[\int_0^t f(x)\, dx]=\frac{F(s)}{s}$$
resultará
$$F(s)\frac{s^2+4}{s}=\frac{1}{s^2}-\frac{1}{s^2+1}+2$$
de donde $$F(s)=\frac{2s^4+2s^2+1}{(s^2+4)s(s^2+1)}$$
Paso 2
Hallar la transformada inversa de $F(s)$. Para ello podemos recurrir a su descomposición en fracciones simples: $$F(s)=\frac{2s^4+2s^2+1}{(s^2+4)s(s^2+1)}=\frac{A}{s}+\frac{Bs+C}{s^2+1}+\frac{Ds+E}{s^2+4}$$ Encuentra el sistema que verifican los coeficientes $A$, $B$, $C$, $D$ y $E$. Pulsa en 'Ver' cuando lo resuelvas.
Ver
Los coeficientes son $$A=\frac{1}{4} \hspace{.3cm} ,\hspace{.3cm} B=\frac{-1}{3}\hspace{.3cm} ,\hspace{.3cm} C=0 \hspace{.3cm} ,\hspace{.3cm}
D=\frac{25}{12} \hspace{.3cm} ,\hspace{.3cm} E=0$$
es decir, $$F(s)=\frac{1}{4s}-\frac{1}{3}\frac{s}{s^2+1}+\frac{25}{12}\frac{s}{s^2+4}$$
Utilizando transformadas de la tabla básica, tendremos
$$f(t)={\cal L}^{-1}[F(s)]=\frac{1}{4}-\frac{1}{3} \cos t +\frac{25}{12} \cos 2t$$
Resolución del segundo apartado: otra opción para resolver la misma ecuación
Paso 1
Derivar una vez todos los miembros de la ecuación $$f'(t)+4\int_0^t f(x)\, dx=t-\mbox{sen}\, t$$ la convertirá en una ecuación diferencial lineal de segundo orden, de coeficientes constantes no homogénea. Encuentra esa ecuación y pulsa en 'Ver'
Ver
La ecuación es $$f''(t)+4f(t)=1-\cos t$$
La solución que buscamos de esa ecuación es aquella que cumple que $f(0)=2$ y que $f'(t)+4\int_0^t f(x)\, dx=t-\mbox{sen}\, t$.
Paso 2
Para encontrar la solución, hemos de resolver primero la ecuación homogénea asociada $$f''_h+4f_h=0$$ Hazlo tú y pulsa en 'Ver'.
Ver
La ecuación característica es $r^2+4=0$, luego la solución general de la homogénea es
$$f_h(t)=C_1\cos 2t+C_2\mbox{sen}\, 2t$$
Paso 3
El siguiente paso es encontrar una solución particular de la completa, $f''(t)+4f(t)=1-\cos t$. Para ello podemos utilizar el método de los coeficientes indeterminados. La solución particular que debemos ensayar es...
$$f_p(t)=A\mbox{sen}\, t+B\cos t$$
$$f_p(t)=A+B\cos 2t$$
Ninguna de las propuestas es correcta.
$$f_p(t)=A+B\cos t$$
Así no es correcta, lo sería añadiendo una constante: $f_p(t)=A\mbox{sen}\, t+B\cos t+C$
No es correcta. En la solución propuesta debemos de alguna manera 'reproducir' las funciones presentes en el término independiente de la ecuación diferencial completa.
Sí hay una propuesta correcta.
En efecto, aunque en principio la propuesta debe ser $f_p(t)=A+B\cos t+C\mbox{sen}\, t$, puesto que en la ecuación diferencial sólo aparece la segunda derivada y no la primera, podemos prescindir del término en seno. Imponiendo que $f''(t)+4f(t)=1-\cos t$, conseguimos los valores de $A$ y $B$:
$$B\cos t+4A+4B\cos t=1-\cos t \hspace{.4cm}\Rightarrow\hspace{.4cm} A=\frac{1}{4}\hspace{.2cm},\hspace{.2cm} B=-\frac{1}{3}$$
Con esto sabemos que una solución particular es $f_p(t)=\frac{1}{4}-\frac{1}{3}\cos t$ y que por tanto la solución general de la ecuación completa es ... Pulsa en 'Continuar' cuando la tengas escrita.
La solución general de la completa es $$f(t)=C_1\cos 2t+C_2\mbox{sen}\, 2t+\frac{1}{4}-\frac{1}{3}\cos t$$
Paso 4
Impondremos ahora que $f(0)=2$, $$f(0)=C_1+\frac{1}{4}-\frac{1}{3}=2\hspace{.4cm}\Rightarrow\hspace{.4cm} C_1=\frac{25}{12}$$ con lo cual, $$f(t)=\frac{25}{12}\cos 2t+C_2\mbox{sen}\, 2t+\frac{1}{4}-\frac{1}{3}\cos t$$ ¿Cómo determinamos el valor de $C_2$? Piénsalo y pulsa en 'Ver'.
Ver
Como efecto de haber derivado la ecuación integro-diferencial, la dimensión del conjunto de soluciones quedó aumentada. Por eso hemos de elegir de entre todas las soluciones anteriores, aquélla que cumple la ecuación inicial, $f'(t)+4\int_0^t f(x)\, dx=t-\mbox{sen}\, t$. Para ello calculamos $f'(t)$, $\int_0^t f(x)\, dx$ e imponenos que cumplan esa ecuación... pulsa en 'Continuar' cuando lo tengas.
Paso 5
Determinar el valor de $C_2$: $$f'(t)=-\frac{25}{6}\mbox{sen}\, 2t+2C_2\cos 2t +\frac{1}{3}\mbox{sen}\, t$$ $$\int_0^t f(x)\, dx=\frac{25}{24}\mbox{sen}\, 2t-\frac{C_2}{2}\cos 2t+\frac{1}{4}t-\frac{1}{3}\mbox{sen}\, t+\frac{C_2}{2}$$ $$f'(t)+4\int_0^t f(x)\, dx=-\mbox{sen}\, t+t+2C_2=t-\mbox{sen}\, t\hspace{.4cm}\Rightarrow\hspace{.4cm} C_2=0$$ Concluimos por tanto que la solución del problema inicial es $$f(t)=\frac{25}{12}\cos 2t+\frac{1}{4}-\frac{1}{3}\cos t$$Representación de la solución y de los términos de la ecuación
En un fichero escribimos las líneas para- generar un vector de valores de $t$ entre $0$ y $4\pi$
- representar puntos de la gráfica de $f(t)=\frac{25}{12}\cos 2t+\frac{1}{4}-\frac{1}{3}\cos t$, en rojo
- representar puntos de la gráfica de $t-\mbox{sen}\, t$, en azul
- representar puntos de la gráfica de $f'(t)=-\frac{25}{6}\mbox{sen}\, 2t+\frac{1}{3}\mbox{sen}\, t$, en verde
- representar puntos de la gráfica de $4\int_0^t f(x)\, dx=\frac{25}{6}\mbox{sen}\, 2t+t-\frac{4}{3}\mbox{sen}\, t$, en magenta
- poner una leyenda en la esquina superior izquierda
- incluir una red de rectas horizontales y verticales ('grid on')
- poner un título
Ver
t=linspace(0,4*pi);
plot(t,25*cos(2*t)/12+1/4-cos(t)/3,'r')
hold on
plot(t,t-sin(t),'b')
plot(t,-25*sin(2*t)/6+sin(t)/3,'g')
plot(t,25*sin(2*t)/6+t-4*sin(t)/3,'m')
legend('solución f(t)','término independiente','f''','4*int(f)_0^t','Location','NorthWest')
title('Componentes de la ecuación f''(t)+4*int(f)_0^t=t-sen t con el dato f(0)=2')
hold off
grid on
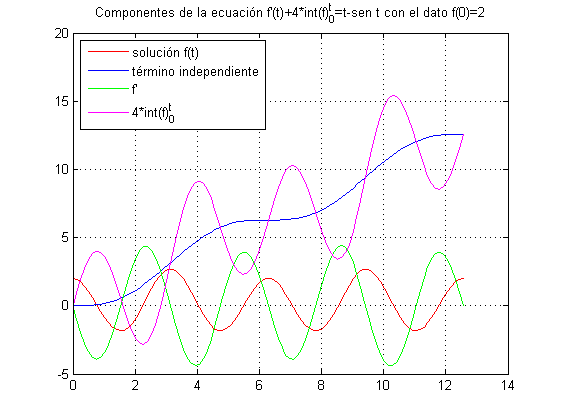
Ejecutando este código obtendremos la figura
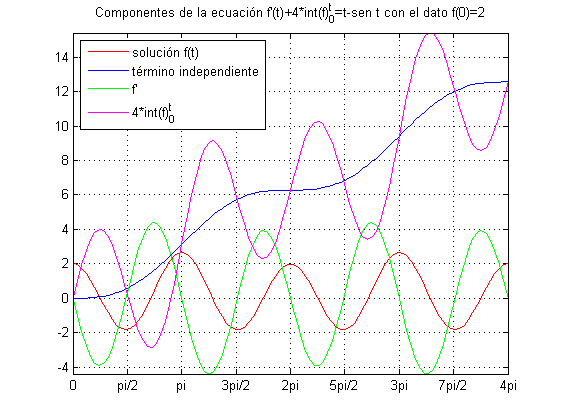
set(gca,'XTick',0:pi/2:4*pi)
set(gca,'XTickLabel',{'0','pi/2','pi','3pi/2','2pi','5pi/2','3pi','7pi/2','4pi'})
Si además queremos que la gráfica se ciña al intervalo $[0,4\pi]$, añadiremos
axis tightLa figura que resulta ahora es