Enunciado
- Utiliza la definición de convolución para hallar la de las funciones
$$f(t)=tU(t-1) \hspace{.5cm} \mbox{y} \hspace{.6cm} g(t)=e^{-3t}U(t)$$
- Comprueba para las funciones anteriores la propiedad de la transformada de Laplace de la convolución.
- Representa en el ordenador las funciones $f(t)$, $g(t)$ y $f*g(t)$ en una misma figura y en otra figura sus funciones transformadas.
Resolución del primer apartado
Paso 1
Utilizando la definición de convolución, sabemos que
$$f*g(t)=\int_0^t tU(t-1)e^{-3(t-x)} \, dt$$
$$f*g(t)=\int_0^t xU(x-1)e^{-3(t-x)} \, dt$$
Ninguna de las propuestas anteriores es correcta.
$$f*g(t)=\int_0^t xU(x-1)e^{-3(t-x)} \, dx$$
No es correcta.
No es correcta.
Sí hay una correcta.
Así es en efecto, y también podemos escribir,
$$f*g(t)=e^{-3t}\int_0^t xU(x-1)e^{3x} \, dx$$
Ahora debemos realizar esa integral, que es la misma que
$$\int_0^t x e^{3x} \, dx$$
$$\int_1^t xe^{3x} \, dx$$
Ninguna de las propuestas es correcta.
Eso sería cierto si lo fuera que $U(x-1)$ es igual a 1 para cualquier $x$ entre 0 y $t$, lo que equivaldría a que $x$ sea mayor que 1 entre 0 y $t$. Pero eso no es verdad para cualquier $t$; si $t$ fuera menor que 1, todos los menores que $t$ serían también menores que 1.
Eligiendo esa opción estás suponiendo que necesariamente $t$ es mayor que 1. ¿Qué pasa si $t$ es menor que 1?
En efecto, ninguna de las propuestas es correcta. Antes de hacer la integral debemos considerar dos casos
- Si $t<1$, todos los $x$ entre 0 y $t$ son menores que 1, luego para ellos $U(x-1)=0$, así que $$f*g(t)=0 \hspace{.4cm} \mbox{si} \hspace{.4cm} t< 1$$
- Si $t>1$, $U(x-1)=0$ para $x<1$, así que $$f*g(t)=e^{-3t} \int_1^t xe^{3x}\, dx \hspace{.4cm} \mbox{si} \hspace{.4cm} t> 1$$
Puesto que $$\int_1^t xe^{3x}\, dx=\left.\frac{1}{3}\left(x-\frac{1}{3}\right)e^{3x}\right]_1^t=
\frac{1}{3}\left[\left(t-\frac{1}{3}\right) e^{3t}-\frac{2}{3}e^3\right]$$
tendremos que para $t>1$,
$$f*g(t)=\frac{1}{3}\left[\left(t-\frac{1}{3}\right )-\frac{2}{3}e^{-3(t-1)}\right]=
\frac{1}{9}\left(3t-1-2e^{-3(t-1)}\right)$$
¿Puedes expresar la función $f*g(t)$ utilizando la función escalón unitario? Piénsalo y pulsa en 'Ver' cuando la hayas escrito.
Ver
Escribiremos $$f*g(t)=\frac{1}{9}\left(3t-1-2e^{-3(t-1)}\right)U(t-1)$$
Resolución del segundo apartado
En este apartado debemos comprobar para estas dos funciones, $f$ y $g$ y para su convolución, la correspondiente propiedad de la transformada de Laplace. Es decir, debemos hacer la transformada de $f$, la de $g$, hacer su producto y comprobar que esta función producto es la transformada de la función convolución:- Transformada de $f(t)=tU(t-1)$: haciendo uso de la tabla básica de transformadas, es ...
$$F(s)=\frac{1}{s^2}$$
$$F(s)=\frac{e^{-s}}{s^2}$$
$$F(s)=e^{-s}\frac{1+s}{s^2}$$
Ésa es la transformada de $tU(t)$, no la de $tU(t-1)$
Ésa es la transformada de $(t-1)U(t-1)$, no la de $tU(t-1)$
En efecto, para poder aplicar la propiedad de traslación en la variable $t$, debemos escribir primero $$f(t)=tU(t-1)=[(t-1)+1]U(t-1)$$ y así
$$f(t)=(t-1)U(t-1)+U(t-1) \hspace{.3cm} \Rightarrow \hspace{.4cm} F(s)=\frac{e^{-s}}{s^2}+\frac{e^{-s}}{s}$$
- Transformada de $g(t)=e^{-3t}U(t)$: según la tabla de transformadas básicas $$G(s)=\frac{1}{s+3}$$
- El producto de las transformadas es $$F(s)G(s)=\frac{1+s}{(s+3)s^2}e^{-s}$$
- La transformada de la convolución $f*g(t)=\frac{1}{9}\left(3t-1-2e^{-3(t-1)}\right)U(t-1)$, es ... Inténtalo tú, teniendo en cuenta que para aplicar la propiedad de traslación, debes escribir toda la expresión $3t-1-2e^{-3(t-1)}$ en términos de $(t-1)$; pulsa en 'Ver' cuando la calcules.
Ver
Puesto que $3t-1=3t-3+2=3(t-1)+2$, escribimos
$$f*g(t)=\frac{1}{9}\left(3(t-1)+2-2e^{-3(t-1)}\right)U(t-1)$$ y así podemos aplicar ya la propiedad de traslación a las conocidas transformadas de $t$, de $1$ y de $e^{-3t}$, (ver tabla)
$${\cal L}[f*g]=\frac{1}{9}\left(\frac{3}{s^2}+\frac{2}{s}-\frac{2}{s+3}\right)e^{-s}$$
que efectivamente podemos agrupar y comprobar que coincide el producto $F(s)G(s)$
$${\cal L}[f*g]=\frac{3(s+3)+2s(s+3)-2s^2}{9s^2(s+3)}e^{-s}=\frac{9s+9+2s^2-2s^2}{9s^2(s+3)}e^{-s}=
\frac{s+1}{s^2(s+3)}e^{-s}$$
Resolución del tercer apartado
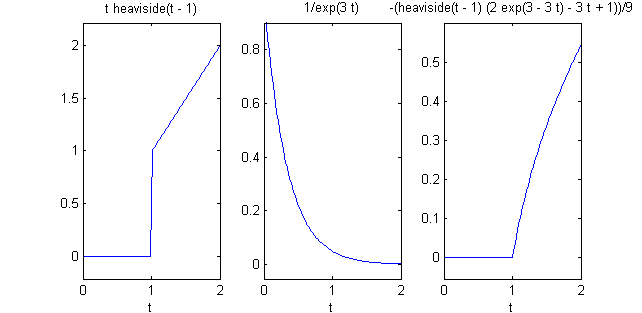
Para representar las funciones $f$, $g$ y $f*g$, recurriremos al comando 'ezplot', pues las dibujaremos como objetos simbólicos; las tres gráficas se representarán en ejes distintos, pero ocupando una misma ventana de figuras, dispuestas con 'subplot' en un array de dimensión 1x3; para introducir la función $U(t)$ utilizaremos la predefinida 'heaviside(t)'. Por todo esto, nuestro fichero empezará porsyms t s figure(1) %% en la figura 1 van f, g y f*g %%%% representación de la función f f=t*heaviside(t-1) subplot(1,3,1) ezplot(f,[0,2])Prepara el resto de la figura 1 y pulsa en 'Ver'.
Ver
el fichero continuará con
%%%% representación de la función g g=exp(-3*t) subplot(1,3,2) ezplot(g,[0,2]) %%%% representación de la función h=f*g h=(3*t-1-2*exp(-3*(t-1)))*heaviside(t-1)/9 subplot(1,3,3) ezplot(h,[0,2])De la ejecución de todas estas líneas resultará
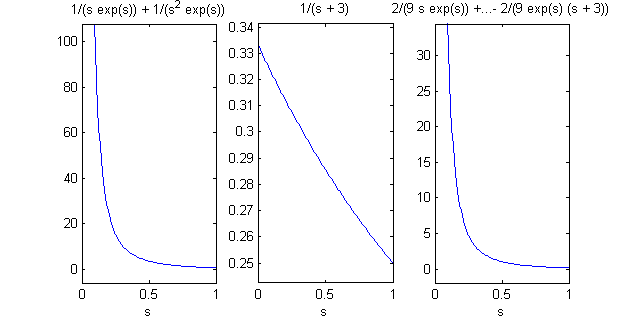
En la figura 2 representaremos siguiendo el mismo proceso las funciones transformadas $F(s)={\cal L}[f]$, $G(s)={\cal L}[g]$ y $F(s)G(s)={\cal L}[f*g]$. Podemos hacerlo en el mismo fichero, observa que en la primera línea ya declaramos 's' como variable simbólica; el fichero puede incluir también el cálculo de las funciones transformadas. Pulsa en 'Ver' cuando lo tengas.
Ver
Si completamos el fichero anterior con las líneas
%%%% cálculo y representación de las transformadas figure(2) %%%% representación de la función F F=laplace(f) subplot(1,3,1) ezplot(F,[0,1]) %%%% representación de la función G G=laplace(g) subplot(1,3,2) ezplot(G,[0,1]) %%%% representación de la función H=FxG H=laplace(h) subplot(1,3,3) ezplot(H,[0,1])al ejecutarlo obtendremos la figura 1 anterior y la nueva, figura 2: