Enunciado
- Aplica transformadas de Laplace para resolver el siguiente problema de valor inicial:
$$y'''(t)-3y(t)=\delta (t-1) \hspace{.3cm}, \hspace{.4cm} y(0)=0 \hspace{.3cm}, \hspace{.4cm} y'(0)=1 \hspace{.3cm}, \hspace{.4cm} y''(0)=-1$$
sabiendo que ${\cal L}[\delta (t-1)]=1$. Utiliza el ordenador para encontrar la solución $y(t)$ a partir de su transformada, $Y(s)$.
- Representa en el ordenador la solución encontrada en el apartado anterior, para valores de $t$ entre $0$ y $2$. Representa también las derivadas primera y segunda.
Resolución del primer apartado
Paso 1
Aplicando transformadas de Laplace a ambos miembros de la ecuación y usando la linealidad de la transformación, $${\cal L}[y''']-3{\cal L}[y]={\cal L}[\delta (t-1)]$$ Debemos ahora hallar la trasformada del segundo término y escribir ${\cal L}[y''']$ en función de $Y(s)={\cal L}[y]$. La transformada de $\delta (t-1)$ la obtenemos a partir de la de $\delta(t)$ mediante la propiedad de traslación en la variable $t$. Hazlo tú y pulsa en 'Ver'.
Ver
La transformada buscada es $${\cal L}[\delta (t-1)]=e^{-s}$$
¿Cómo escribimos ${\cal L}[y''']$ en función de $Y(s)={\cal L}[y]$? Debemos recurrir a la transformada de la derivada. Puesto que la derivada tercera es la derivada segunda de la primera derivada, escribimos
$${\cal L}[y''']={\cal L}[(y')'']=s^2{\cal L}[y']-y'(0) s-y''(0)=s^2(s{\cal L}[y]-y(0))-y'(0) s-y''(0)$$ o bien
$${\cal L}[y''']=s^3{\cal L}[y]-y(0)s^2-y'(0) s-y''(0)$$
suponiendo que tanto $y$, como $y'$, como $y''$ son continuas en $t=0$. Si no fuera así, cambiaríamos los valores en el cero por los límite por la derecha. Así pues, la ecuación para la transformada es, ... escríbela y pulsa en 'Continuar' cuando la tengas.
La ecuación para $Y(s)$ es $$s^3Y(s)-s+1-3Y(s)=e^{-s}$$ o bien $$(s^3-3)Y(s)-s+1=e^{-s}$$
Paso 2
Despejar en esa ecuación algebraica la función $Y(s)$: $$Y(s)=\frac{e^{-s}+s-1}{s^3-3}$$Paso 3
Hallar la transformada inversa, $y(t)={\cal L}^{-1}[Y(s)]$. Para hacerlo a mano haríamos la transformada inversa de $$\frac{s-1}{s^3-3}$$ y de $$\frac{1}{s^3-3}$$ mediante descomposición en fracciones simples y después utilizaríamos las transformadas de la exponencial, el seno y el coseno y las propiedades de traslación. Para hacerlo en el ordenador, escribiremossyms s y= ilaplace((exp(-s)+s-1)/(s^3-3))
Resolución del segundo apartado
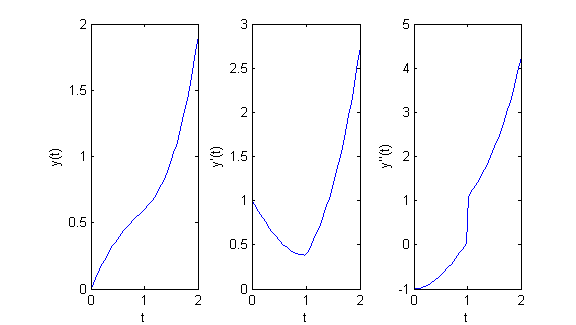
Como has podido comprobar, la respuesta del ordenador en el apartado anterior es una función un tanto oscura. Si queremos una expresión más clara podríamos hacerla por partes, bien a mano o bien utilizando el ordenador en cada parte. Si queremos ver una representación podemos hacerlo de la siguiente manera: generar un vector de valores de $t$, generar después los correspondientes valores de $y(t)$ y representar éstos frente a aquéllos. Haremos lo mismo con la primera y segunda derivada. Inténtalo y pulsa en 'Ver' cuando lo tengas.
Ver
syms s t
y= ilaplace((exp(-s)+s-1)/(s^3-3)); %% función y(t)
dy=diff(y); %% función y'(t)
d2y=diff(dy);
%%% generamos un vector de t y los correspondientes para y, y' e y''
vt=linspace(0,2,50);
vy=subs(y,t,vt);
vdy=subs(dy,t,vt);
vd2y=subs(d2y,t,vt);
%%% representamos esos vectores (de y, y' e y'') para t entre 0 y 2
subplot(1,3,1)
plot(vt,vy); xlabel('t'); ylabel('y(t)')
subplot(1,3,2)
plot(vt,vdy);xlabel('t'); ylabel('y''(t)')
subplot(1,3,3)
plot(vt,vd2y);xlabel('t'); ylabel('y''''(t)')
El resultado es la siguiente figura