Enunciado
Encuentra la transformada inversa de $$F(s)=\frac{e^{2-s/2}}{\sqrt{(s+3)^3}}\mbox{Sh}(4+\frac{s}{2})$$ Comprueba el resultado con el ordenador y representa las funciones $F(s)$ y ${\cal L}^{-1}[F]$.
Paso 1
Escribir la función $F(s)$ en términos de funciones más habituales, cambiando la función seno hiperbólico por su expresión en términos de la exponencial: $$\mbox{Sh}(u)=\frac{e^u-e^{-u}}{2}$$ Haz este paso y pulsa en 'Ver'.
Ver
$$e^{2-s/2}\mbox{Sh}(4+\frac{s}{2})=e^{2-s/2}\frac{e^{4+s/2}-e^{-(4+s/2)}}{2}=\frac{e^2}{2}e^{-s/2}(e^4e^{s/2}-e^{-4}e^{-s/2})=$$
$$=\frac{e^2}{2}(e^4-e^{-4e^{-s}})=\frac{1}{2}(e^6-e^{-2}e^{-s})$$
luego $$F(s)=\frac{e^6-e^{-2}e^{-s}}{2\sqrt{(s+3)^3}}=\frac{e^6}{2}\frac{1}{\sqrt{(s+3)^3}}-\frac{e^{-2}}{2}\frac{e^{-s}}{\sqrt{(s+3)^3}}=\frac{e^6}{2}G(s)-\frac{e^{-2}}{2}e^{-s}G(s)$$
donde
$$G(s)=\frac{1}{\sqrt{(s+3)^3}}$$
Paso 2
Hallar $g(t)={\cal L}^{-1}[G(s)]$. Puesto que $G(s)$ es un desplazamiento de $H(s)=s^{-3/2}$...
Ninguna de las opciones es correcta.
$$g(t)=e^{3t}{\cal L}^{-1}[H(s)]$$
$$g(t)=e^{-3s}{\cal L}^{-1}[H(s)]$$
$$g(t)=e^{-3t}{\cal L}^{-1}[H(s)]$$
Sí hay una correcta.
¡Cuidado con el signo del factor de traslación!
¡Cuidado con el nombre de las variables!
En efecto, eso es correcto por la propiedad de traslación en la variable $s$. La inversa de $H(s)$ la obtenemos de la
tabla básica de transformadas; escribe $g(t)$ y pulsa en 'Continuar'.
$$g(t)=e^{-3t}{\cal L}^{-1}[H(s)]=e^{-3t}\frac{2}{\sqrt{\pi}}\sqrt{t}$$
Paso 3
Teniendo en cuenta que $$F(s)=\frac{e^6}{2}G(s)-\frac{e^{-2}}{2}e^{-s}G(s)$$ hallar la transformada inversa de $F(s)$ conocida la de $G(s)$. Por una parte, $${\cal L}^{-1}[\frac{e^6}{2}G(s)]=\frac{e^6}{2}{\cal L}^{-1}[G(s)]=\frac{e^6}{2}g(t)= e^{6-3t}\sqrt{\frac{t}{\pi}}$$ Sólo falta por tanto calcular la inversa de $e^{-s}G(s)$. Hazlo tú y pulsa en 'Ver'.
Ver
Aplicando la propiedad de traslación en la variable $t$,
$${\cal L}^{-1}[e^{-s}G(s)]=g(t-1)U(t-1)=e^{-3(t-1)}\frac{2}{\sqrt{\pi}}\sqrt{t-1}\,U(t-1)$$
con lo cual
$${\cal L}^{-1}[\frac{e^{-2}}{2}e^{-s}G(s)]=e^{1-3t}\sqrt{\frac{t-1}{\pi}}\,U(t-1)$$ y el resultado final para $f(t)$ es
$$f(t)=e^{6-3t}\sqrt{\frac{t}{\pi}}-e^{1-3t}\sqrt{\frac{t-1}{\pi}}\,U(t-1)$$
Paso 4
Comprobación del resultado con el ordenador y representación de las funciones. Escribe en un fichero las líneas de código con las que- declaras 's' como variable simbólica
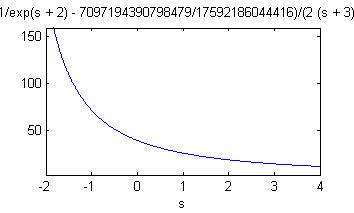
- defines 'F' como $F(s)=\frac{e^6-e^{-2-s}}{2\sqrt{(s+3)^3}}$
- activas la figura 1 ('figure(1)')
- dibujas con 'ezplot' la función 'F' entre $-2$ y 4
- activas la figura 2
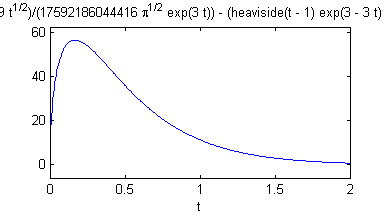
- defines 'f' como la transformada inversa de 'F' (con 'ilaplace')
- dibujas con 'ezplot' la función 'F' entre 0 y 2
Ver
syms s F=(exp(6)-exp(-2-s))/(2*(s+3)^(3/2)); figure(1) ezplot(F,[-2,4]) figure(2) f=ilaplace(F) ezplot(f,[0,2])Cuando ejecutemos este fichero, obtendremos en la ventana de comandos la transformada inversa:
(7097194390798479*t^(1/2))/(17592186044416*pi^(1/2)*exp(3*t)) - (heaviside(t - 1)*exp(3 - 3*t)*(t - 1)^(1/2))/(pi^(1/2)*exp(2))Para ver mejor esta expresión podemos poner
pretty(f)obteniendo
1/2 1/2
7097194390798479 t heaviside(t - 1) exp(3 - 3 t) (t - 1)
----------------------------- - ----------------------------------------
1/2 1/2
17592186044416 pi exp(3 t) pi exp(2)
donde está tomando $7097194390798479/17592186044416$ como $e^6$.
En la ventana 'Figure 1' tenemos la representación de $F(s)$: