Índice de tema

 

Enunciado

Sea \(H\) el sólido encerrado en \(x\geq 0\) por $$x+\frac{3}{4}y^2=3$$ limitado inferiormente por \(z=0\) y superiormente por $$\frac{2}{3}x+z=4$$ Halla el volumen de este sólido.

Paso 1

¿Qué hemos de integrar? Si no sabes por dónde empezar puedes mirar las interpretaciones de la integral doble. En este caso el sólido "comienza" en \(z=0\) y "termina" en \(z=4-2x/3\) para \((x,y)\) en cierto conjunto \(D\) del plano, luego la integral doble que expresa su volumen es... escríbelo y pulsa en 'Ver'
Ver
$$\mbox{Volumen}=\int\!\!\int_D \left(4-\frac{2}{3} x\right)\, dA$$

Paso 2

¿Cuál es la región de integración, \(D\)? Lateralmente el sólido está limitado por el plano \(x=0\) y por el cilindro (parabólico) \(x+3y^2/4=3\), luego \(D\) es el conjunto $$D=\{(x,y) / \ x\geq 0,\ x+\frac{3}{4} y^2 \leq 3\}$$

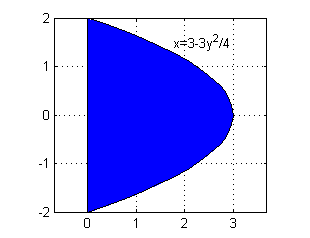
Gráfica

Esta figura, salvo la ecuación de la curva que encierra el dominio por la derecha, se ha realizado con las siguientes órdenes 
y=-2:.1:2;
fill(3-3*y.^2/4,y,'b')
axis equal
grid on
Ahora debemos prepararlo para hacer sobre él las integrales iteradas, escoge:
$$D=\{(x,y) / \, 0\leq y\leq 2 ,\, 0 \leq x \leq x+\frac{3}{4} y^2\}$$
$$D=\{(x,y) / \, 0\leq y\leq 2 ,\, 0 \leq x \leq 3-\frac{3}{4} y^2\}$$
$$D=\{(x,y) / \, -2\leq y\leq 2 ,\, 0 \leq x \leq 3-\frac{3}{4} y^2\}$$
¡No! no tiene ningún sentido
No, puesto que también hay región para \(y\leq 0\)
En efecto, esa es la región. Ahora debemos escribir las integrales iteradas. Escríbelas y pulsa en 'Continuar' cuando lo tengas.

Paso 3

Tenemos $$\mbox{Volumen}=\int\!\!\int_D \left(4-\frac{2}{3} x\right)\, dA= \int_{-2}^2 \int_0^{3-\frac{3}{4} y^2}\left(4-\frac{2}{3} x\right)\, dx\, dy$$ El cálculo se simplifica si tenemos en cuenta que el integrado y los límites de integración en la variable \(y\) son funciones pares en \(x\), con lo cual $$\mbox{Volumen}= 2\int_0^2 \int_0^{3-\frac{3}{4} y^2}\left(4-\frac{2}{3} x\right)\, dx\, dy$$ Calcula esta última expresión y pulsa en 'Continuar' cuando la tengas.
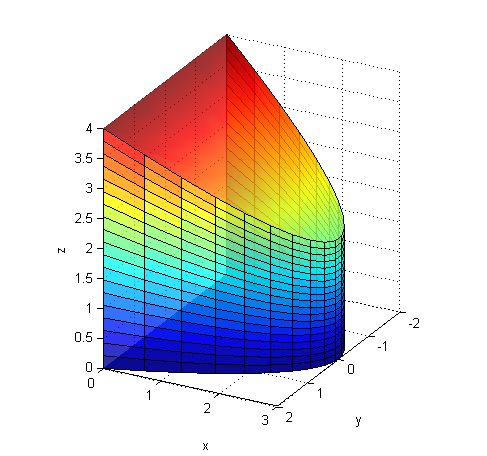
$$\mbox{Volumen}=2\int_0^2 \left[4x-\frac{x^2}{3} \right]_0^{3-\frac{3}{4} y^2}\, dy=$$ $$=6\int_0^2 \left(3-\frac{y^2}{2}-\frac{y^4}{16} \right)\, dy=\frac{128}{5}$$ En la siguiente figura puedes ver el sólido cuyo volumen has calculado:

Gráfica

Resumen

  1. Determinar qué hay que integrar
  2. Escribir la región donde hay que integrar y plantear iteradas
  3. Calcular las integrales iteradas.