Enunciado
Si $(u,v)$ son las variables resultantes de un giro de ángulo $\alpha$ de las variables $(x,y)$, es porque
$$x=u\cos\alpha-v\, \mbox{sen}\, \alpha \ \hspace{.6cm} \mbox{y}\ \hspace{.6cm} y=u\, \mbox{sen}\, \alpha+v\cos\alpha$$
- Efectúa un giro de ángulo $\alpha=\frac{\pi}{4}$ radianes a la función $z=y^2-x^2$ y comprueba que la expresión para el cuadrado del módulo del gradiente de $z$ es la misma para las variables $x$, $y$ que para las variables resultantes del giro, $u$ y $v$.
- Comprueba que para una función cualquiera, $z=f(x,y)$ suficientemente derivable, la función $g(x,y)=(z'_x)^2+(z'_y)^2$ es invariante frente a giros.
- Comprueba que lo mismo ocurre con el laplaciano: $\Delta z=z''_{xx}+z''_{yy}$.
Resolución del primer apartado
El cuadrado del módulo del gradiente de $z=y^2-x^2$ es:
$$z'_x=-2x \ , \ z'_y=2y \ \ \Rightarrow \ \ g(x,y)=4x^2+4y^2$$
Escribe las ecuaciones que relacionan $x$ e $y$ con las variables $u$ y $v$ en un giro de ángulo $\alpha=\frac{\pi}{4}$ radianes. Pulsa en 'Ver' cuando las tengas.
Ver
Efectivamente,
$$x=\frac{\sqrt{2}}{2}(u-v) \ \hspace{.6cm} \mbox{y}\ \hspace{.6cm} y=\frac{\sqrt{2}}{2}(u+v)$$
Ahora sustituimos $x$ e $y$ por estas expresiones para encontrar $h(u,v)=f(x(u,v),y(u,v))$:
$$h(u,v)=\frac{1}{2}(u+v)^2-\frac{1}{2}(u-v)^2=2uv$$
y calculamos el cuadrado del módulo del gradiente de $z=h(u,v)$:
$$g(u,v)=4u^2+4v^2$$
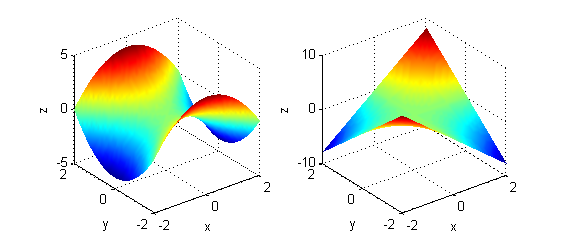
En la siguiente figura puedes ver a la izquierda la gráfica de $z=y^2-x^2$ para $x\in[-2,2]$ e $y\in[-2,2]$ y a la derecha la de $z=2xy$ para $x\in[-2,2]$ e $y\in[-2,2]$:
A estas gráficas les superponemos la de la función cuadrado del módulo del gradiente:
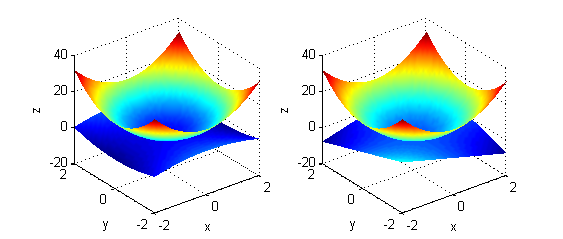

A estas gráficas les superponemos la de la función cuadrado del módulo del gradiente:

Resolución del segundo apartado
Lo que se pide en este apartado es comprobar que $(z'_u)^2+(z'_v)^2=(z'_x)^2+(z'_y)^2$. Para ello debemos escribir $(z'_u)^2+(z'_v)^2$ en las variables $x$ e $y$. Siguiendo la derivación compuesta de dos variables, tendremos $$z'_u=z'_x x'_u+z'_y y'_u \ \ \ \mbox{y} \ \ \ z'_v=z'_x x'_v+z'_y y'_v$$ Calcula las parciales de $x$ e $y$ respecto de $u$ y $v$ y sustitúyelas en las expresiones anteriores. Luego pulsa en 'Ver'.
Ver
$$x'_u=\cos\alpha \ ,\ \ y'_u=\mbox{sen}\,\alpha\ ,\ \ x'_v=-\mbox{sen}\,\alpha\ ,\ \ y'_v=\cos \alpha$$
con lo cual
$$z'_u=z'_x \cos \alpha +z'_y\,\mbox{sen}\, \alpha \ \ \ \mbox{y} \ \ \
z'_v=z'_x (- \mbox{sen}\,\alpha) +z'_y\cos \alpha$$
Ahora sólo falta hacer $(z'_u)^2+(z'_v)^2$:
$$(z'_u)^2+(z'_v)^2=(z'_x)^2\cos^2 x+ (z'_y)^2\mbox{sen}^2\,\alpha + (z'_x)^2\mbox{sen}^2\,\alpha+(z'_y)^2\cos \alpha=(z'_x)^2+(z'_y)^2$$
Resolución del segundo apartado
En este caso debemos escribir las parciales $z''_{uu}$ y $z''_{vv}$ en función de las variables $x$ e $y$. Utilizando de nuevo las reglas de derivación compuesta, $$z''_{uu}= (z'_u)'_xx'_u+(z'_u)'_yy'_u=(z''_{xx}\cos \alpha +z''_{yx}\mbox{sen}\,\alpha)\cos \alpha+(z''_{xy}\cos\alpha+z''_{yy}\mbox{sen}\,\alpha)\mbox{sen}\,\alpha$$ Suponemos que se cumplen las condiciones suficientes para que $z''_{yx}=z''_{xy}$ del teorema de Schwarz, de forma que la expresión anterior es $$z''_{uu}=z''_{xx}\cos^2 \alpha+2z''_{xy}\mbox{sen}\,\alpha\cos \alpha+z''_{yy}\mbox{sen}^2\,\alpha$$ Ahora haz tú lo mismo para $z''_{vv}$ y pulsa en 'Continuar'
$$z''_{vv}= (z'_v)'_xx'_v+(z'_v)'_yy'_v=(-z''_{xx}\mbox{sen}\,\alpha +z''_{yx}\cos\alpha)(-\mbox{sen}\,\alpha)+(-z''_{xy}\mbox{sen}\,\alpha+z''_{yy}\cos \alpha)\cos\alpha$$
o bien
$$z''_{vv}= z''_{xx}\mbox{sen}^2\,\alpha -2z''_{xy}\mbox{sen}\,\alpha\cos \alpha+z''_{yy}\cos^2 \alpha$$
Sólo falta hacer la suma, para comprobar que efectivamente
$$(z''_{uu})^2+(z''_{vv})^2=(z''_{xx})^2+(z''_{yy})^2$$
es decir, el laplaciano es invariante frente a giros.