Enunciado
- Escribe la expresión equivalente a $$z''_{xx}=z''_{yy}$$ para las variables $u$ y $v$ si
$$x=u+v\ \hspace{.5cm} \mbox{e}\ \hspace{.5cm} \ y=u-v$$
- Encuentra todas las funciones $z=z(x,y)$ que verifican que $z''_{xx}=z''_{yy}$.
- Dibuja la gráfica de una de esas funciones, la que tú quieras, y de su correspondiente derivada segunda respecto de $x$.
Resolución del primer apartado
Paso 1
En este caso es sencillo encontrar las variables $u$ y $v$ en función de las variables $x$ e $y$: $$\left.\begin{array}{ll}x=u+v \\ y=u-v\end{array}\right|\hspace{.5cm} \Rightarrow \hspace{.5cm} \begin{array}{ll} u=\frac{1}{2}(x+y)\\ v=\frac{1}{2}(x-y)\end{array}$$ Puesto que $z$ es función de $x$ e $y$, siendo $x$ e $y$ funciones de $u$ y $v$, y deben escribirse las derivadas $z''_{xx}$ y $z''_{yy}$ utilizando las derivadas de $z$ respecto de $u$ y $v$, debemos seguir la derivación compuesta de dos variables .Paso 2
Necesitaremos las derivadas de $u$ y $v$ respecto de $x$ e $y$. Hazlas y pulsa en 'Continuar'.
Es fácil obtener que $$u'_x=\frac{1}{2} \ \ \ ,\ \ \ \ u'_y=\frac{1}{2}$$ y que
$$v'_x=\frac{1}{2} \ \ \ ,\ \ \ \ v'_y=\frac{-1}{2}$$
Paso 3
Ahora expresaremos $z'_{x}$ y $z'_y$ en función de $u$ y $v$: $$z'_x=z'_uu'_x+z'_vv'_x=\frac{1}{2}(z'_u+z'_v)$$ $$z'_y=z'_uu'_y+z'_vv'_y=\frac{1}{2}(z'_u-z'_v)$$ Ahora haz tú lo mismo para $z''_{xx}$ y $z''_{yy}$ y pulsa en 'Continuar' cuando lo tengas.
$$z''_{xx}=(z'_x)'_uu'_x+(z'_x)'_vv'_x=\frac{1}{2}(z''_{uu}+z''_{vu})u'_x+\frac{1}{2}(z''_{uv}+z''_{vv})v'_x=\frac{1}{4}(z''_{uu}+z''_{vu})+\frac{1}{4}(z''_{uv}+z''_{vv})$$
$$z''_{yy}=(z'_y)'_uu'_y+(z'_y)'_vv'_y=\frac{1}{2}(z''_{uu}-z''_{vu})u'_y+\frac{1}{2}(z''_{uv}-z''_{vv})v'_y=\frac{1}{4}(z''_{uu}-z''_{vu})-\frac{1}{4}(z''_{uv}-z''_{vv})$$
Ahora debemos tener en cuenta el teorema de Schwarz sobre derivadas segundas cruzadas, con lo cual
$$z''_{xx}=\frac{1}{4}(z''_{uu}+2z''_{uv}+z''_{vv})$$
$$z''_{yy}=\frac{1}{4}(z''_{uu}-2z''_{uv}+z''_{vv})$$
Sólo queda sustituir en la expresión $z''_{xx}=z''_{yy}$:
$$z''_{xx}=z''_{yy} \hspace{.4cm} \Rightarrow \hspace{.4cm} z''_{uv}=0$$
Resolución del segundo apartado
Para encontrar todas las funciones $z=z(x,y)$ que cumplen que $z''_{xx}=z''_{yy}$, utilizamos el apartado anterior, ya que la ecuación equivalente, $z''_{uv}=0$, es más sencilla de resolver.Paso 1
Escoge cúales son todas las funciones que cumplen $z''_{uv}=0$:
funciones de la forma $z(u,v)=f(u)g(v)$
funciones de la forma $z(u,v)=f(u)/g(v)$
funciones de la forma $z(u,v)=f(u)+g(v)$
No es correcto: $z'_u=f'(u)g(v)$ y $z''_{uv}=f'(u)g'(v)$ Sólo valdría para las funciones tales que $f'(u)$ o $g'(v)$ sean nulas.
No es correcto: $z'_u=f'(u)/g(v)$ con lo cual $z''_{uv}$ no tiene por qué ser nula.
En efecto, ya que $z'_u=f'(u)$ y $z''_{uv}=0$ para cualesquiera $f$ y $g$.
Paso 2
Ahora debemos escribir la expresión $z(u,v)=f(u)+g(v)$ de nuevo en las variables $x$ e $y$, teniendo en cuenta que $u=\frac{1}{2}(x+y)$ y $v=\frac{1}{2}(x-y)$. Hazlo tú y pulsa en 'Ver'
Ver
Todas las funciones que cumplen que $z''_{xx}=z''_{yy}$ son de la forma $$z(x,y)=f(\frac{x+y}{2})+g(\frac{x-y}{2})$$ Puesto que $f$ y $g$ son cualesquiera, podemos incluir $1/2$ en ellas, de manera que la forma general para las funciones que satisfacen que $z''_{xx}=z''_{yy}$ es
$$z(x,y)=f(x+y)+g(x-y)$$
Resolución del tercer apartado
Elegimos dos funciones $f$ y $g$ cualesquiera, dentro de que sean derivables por supuesto. Podemos tomar $f(t)=\cos t$ y $g(t)=\cos^2 t$. La función resulta $$z(x,y)=f(x+y)+g(x-y)=\cos(x+y)+\cos^2(x-y)$$ Su derivada $z''_{xx}$ es $$z''_{xx}=-\cos(x+y)-2\cos 2(x-y)$$ Escribe las líneas de código para dibujar una porción de la gráfica de estas funciones y pulsa en 'Ver'.
Ver
Ejecutando
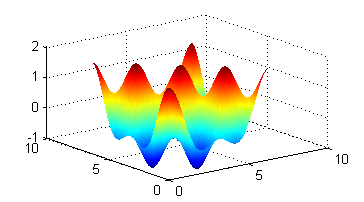
y ésta es la segunda derivada respecto de $x$:
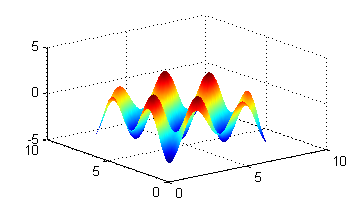
[X,Y]=meshgrid(0:.1:2*pi); figure(1) surf(X,Y,cos(X+Y)+(cos(X-Y).^2)) shading interp figure(2) surf(X,Y,-cos(X+Y)-2*cos(2*(X-Y))) shading interpse obtiene la siguiente gráfica en la ventana 'Figura 1'

y ésta es la segunda derivada respecto de $x$:
