Enunciado
En este ejercicio vamos a suponer que el precio $p$, en cientos de euros, de un piso en una determinada ciudad depende de
- $s=$ precio del m$^2$ de suelo, en euros
- $m=$ precio medio del m$^3$ de los materiales, en euros
- $a=$ superficie del piso, en m$^2$
es decir, $$p=f(s,m,a)$$
Consideramos los siguientes valores para estas variables
$$s=500\ \ ,\ \ m=1000\ \ ,\ \ a=90$$
y la siguiente información, siempre relativa a esos valores de las variables
- la máxima tasa de cambio de $p$ es 3;
- si los precios $s$ y $m$ aumentan en la misma proporción, la tasa de cambio de $p$ es $6\frac{\sqrt{5}}{5}$.
Con estos datos,
- Halla la tasa de cambio de $p$ cuando $s$ aumenta el doble que $m$, sabiendo que esta tasa es mayor que la tasa de cambio de $p$ cuando $m$ aumenta el doble que $s$.
- Encuentra la proporción en que deben cambiar $s$ y $m$ para que el cambio de $p$ sea máximo.
- ¿En cuántos euros puede modificarse el precio $p$ si el precio del suelo fluctúa hasta $3$ euros y el de los materiales hasta $10$ euros (en ambos precios la fluctuación puede ser hacia arriba o hacia abajo)?
Resolución del primer apartado
Una tasa, razón o velocidad de cambio es una derivada direccional. Así pues, parece que tendremos que empezar encontrando el gradiente, esto es, las derivadas parciales $p'_s$ y $p'_m$.
Paso 1
Puesto que no disponemos de la expresión de la función $p$, el primer paso es escribir en términos de estas parciales la información que el enunciado nos da en términos de tasas de cambio. Inténtalo y pulsa en 'Ver'.
Ver
- la máxima tasa de cambio de $p$ es 3; teniendo en cuenta las propiedades del gradiente , esto significa que $$(p'_s)^2+(p'_m)^2=9$$
- si los precios $s$ y $m$ aumentan en la misma proporción, la tasa de cambio de $p$ es $6\frac{\sqrt{5}}{5}$; ¿respecto de qué dirección tiene la derivada direccional este valor? o dicho de otro modo ¿qué dirección en el plano $(s,m)$ es aquella en que $s$ y $m$ aumentan en la misma proporción? Debemos encontrar el vector de módulo 1 correspondiente a la bisectriz del plano, es decir $${\bf u}_1=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$$ La derivada direccional respecto de esta dirección es $$D_{{\bf u}_1}p=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\cdot (p'_s,p'_m)=\frac{\sqrt{2}}{2}(p'_s+p'_m)$$
Paso 2
Resolución del sistema: Si por ejemplo de la segunda ecuación despejamos $p'_s$ y lo introducimos en la primera, resulta $$10(p'_m)^2-12\sqrt{10} p'_m+27=0$$ de donde $p'_m=3\frac{\sqrt{10}}{10}$ o $p'_m=9\frac{\sqrt{10}}{10}$. Con estos valores y la segunda ecuación del sistema, sacamos los de $p'_s$. De manera que el gradiente de $p$ es $$\nabla p= 3\frac{\sqrt{10}}{10}(3,1) \hspace{.3cm} \mbox{o bien} \hspace{.3cm} \nabla p= 3\frac{\sqrt{10}}{10}(1,3)$$ ¿Cómo sabremos cuál es? En el enunciado del primer apartado indica que la tasa de cambio de $p$ cuando $s$ aumenta el doble que $m$ es mayor que la tasa de cambio de $p$ cuando $m$ aumenta el doble que $s$. Escribamos esta información en términos de derivadas direccionales para ver si eso nos ayuda.Paso 3
Escribimos las tasas de cambio descritas en el primer apartado en términos de derivadas direccionales:- ¿Cuál es la dirección del plano $(s,m)$ si $s$ aumenta el doble que $m$? Escríbela y pulsa en 'Continuar'.
En efecto, la dirección en que ocurre eso es $${\bf u}_2=(2\frac{\sqrt{5}}{5},\frac{\sqrt{5}}{5})$$
y la correspondiente derivada direccional es
$$D_{{\bf u}_2}p=(2\frac{\sqrt{5}}{5},\frac{\sqrt{5}}{5})\cdot (p'_s,p'_m)=\frac{\sqrt{5}}{5}(2p'_s+p'_m)$$
- ¿Cuál es la dirección del plano $(s,m)$ si $m$ aumenta el doble que $s$? en este caso tendremos la dirección $${\bf u}_3=(\frac{\sqrt{5}}{5},2\frac{\sqrt{5}}{5})$$ y la correspondiente derivada direccional es $$D_{{\bf u}_3}p=(\frac{\sqrt{5}}{5},2\frac{\sqrt{5}}{5})\cdot (p'_s,p'_m)=\frac{\sqrt{5}}{5}(p'_s+2p'_m)$$ Piensa cómo utilizar estas dos derivadas direccionales para deducir los valores de $p'_s$ y de $p'_m$ y pulsa en 'Continuar'.
$$D_{{\bf u}_2}p > D_{{\bf u}_3}p \hspace{.3cm} \Rightarrow \hspace{.3cm}
2p'_s+p'_m>p'_s+2p'_m \hspace{.3cm} \Rightarrow \hspace{.3cm} p'_s>p'_m$$
y por tanto
$$p'_s=9\frac{\sqrt{10}}{10} \hspace{.5cm} \mbox{y} \hspace{.5cm} p'_m=3\frac{\sqrt{10}}{10}$$
y la tasa de cambio pedida en el primer apartado es
$$D_{{\bf u}_2}p=\frac{\sqrt{5}}{5}\frac{\sqrt{10}}{10}(2\cdot 9+3)=21\frac{\sqrt{2}}{10}$$
Resolución del segundo apartado
Por las propiedades del gradiente sabemos que para que el cambio de $p$ sea máximo, la dirección debe ser la misma que le corresponde al gradiente. Por tanto, la relación entre lo que cambia $s$ y lo que cambia $m$ para que sea máximo el cambio de $p$ es
$$\frac{p'_s}{p'_m}=\frac{1}{\sqrt{2}}$$
$$\frac{p'_s}{p'_m}=\frac{1}{3}$$
Ninguna de las opciones propuestas es correcta.
$$\frac{p'_s}{p'_m}=3$$
¿Cómo sale ese valor? Debes mirar la relación entre las componentes del gradiente.
Hay un fallo, míralo bien.
Sí que hay una opción correcta.
Sí, esto es lo correcto, pues 3 es la relación entre las dos componentes del vector gradiente y esa relación se mantendrá así en toda la recta del plano $(s,m)$ que tiene como vector director ese gradiente. Para los valores $s=500$, $m=1000$ y $a=90$ el mayor aumento del precio del piso (dejando $a$ constante) se producirá cuando el precio del suelo aumente el triple que el precio de los materiales.
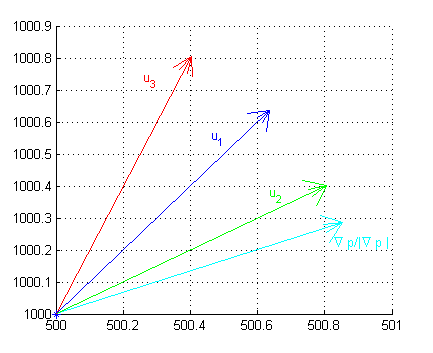
En la siguiente figura se han dibujado las cuatro direcciones con las que has trabajado en estos apartados:
$${\bf u_1}=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}) ,\hspace{.4cm} {\bf u_2}=(2\frac{\sqrt{5}}{5},\frac{\sqrt{5}}{5}), \hspace{.4cm} {\bf u_3}=(\frac{\sqrt{5}}{5},2\frac{\sqrt{5}}{5}),
\hspace{.4cm} \frac{\nabla p}{|\nabla p|}=(3\frac{\sqrt{10}}{10},\frac{\sqrt{10}}{10})$$
Observa que están en las rectas de pendientes $1$, $1/2$, $2$ y $1/3$ respectivamente.
Y a continuación puedes ver los vectores tangentes correspondientes a esas direcciones; observa cómo la tercera componente máxima es la que acompaña a $\frac{\nabla p}{|\nabla p|}$:
$$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},6\frac{\sqrt{5}}{5}) ,\hspace{.4cm} (2\frac{\sqrt{5}}{5},\frac{\sqrt{5}}{5},21\frac{\sqrt{2}}{10}) ,\hspace{.4cm} (\frac{\sqrt{5}}{5},2\frac{\sqrt{5}}{5},3\frac{\sqrt{2}}{2}),
\hspace{.4cm} (3\frac{\sqrt{10}}{10},\frac{\sqrt{10}}{10},3)$$
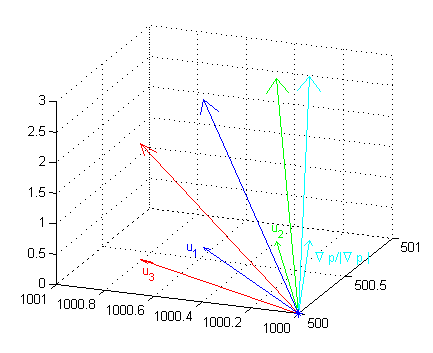
plot3(500,1000,0,'*') hold on quiver3(500,1000,0,1/sqrt(2),1/sqrt(2),0,'b') quiver3(500,1000,0,1/sqrt(2),1/sqrt(2),6/sqrt(5),'b') quiver3(500,1000,0,2/sqrt(5),1/sqrt(5),0,'g') quiver3(500,1000,0,2/sqrt(5),1/sqrt(5),21*sqrt(2)/10,'g') quiver3(500,1000,0,1/sqrt(5),2/sqrt(5),0,'r') quiver3(500,1000,0,1/sqrt(5),2/sqrt(5),3/sqrt(2),'r') quiver3(500,1000,0,3/sqrt(10),1/sqrt(10),0,'c') quiver3(500,1000,0,3/sqrt(10),1/sqrt(10),3,'c') hold off grid on
Resolución del tercer apartado
Para determinar cuánto puede fluctuar, aproximadamente, el precio $p$ conociendo el margen de variación de $s$ y $m$, utilizaremos la diferencial escrita con el gradiente. Escribe en este caso la expresión de la diferencial en función de las parciales obtenidas antes y calcúlala.
Puesto que $\Delta s=3$, $\Delta m=10$, $p'_s=9\frac{\sqrt{10}}{10}$, $p'_m=3\frac{\sqrt{10}}{10}$,
$$dp=p'_s\Delta s+p'_m\Delta m=\frac{\sqrt{10}}{10}(9\cdot 3+3\cdot 10)=57\frac{\sqrt{10}}{10}\approx 18.0250$$
Dado que este número está en cientos de euros, el precio puede fluctuar aproximadamente $1802$ euros.
Resumen
- Primer apartado
- escribir para las parciales la información da el enunciado en términos de tasas
- resolver el sistema de ecuaciones para obtener las parciales
- expresar las tasas del primer apartado en términos de derivadas direccionales para fijar las parciales y terminar el apartado.
- Segundo apartado
- únicamente debe buscarse la relación entre las componentes del gradiente
- Tercer apartado
- hallar el valor de la diferencial correspondiente a esos incrementos.