Enunciado
Llamamos $S$ a la superficie $x^2+y^2+z^2=4$. En $S$ nos situamos en el punto $P(1,-1,\sqrt{2})$.
- Dibuja una porción de la superficie $S$ que contenga al punto $P$, la curva de nivel que pasa por el punto $(1,-1)$ y el gradiente de $z$ en ese punto.
- Halla la ecuación del plano tangente a $S$ en $P$.
- Llamamos $C$ a la curva contenida en $S$ que dibujaríamos si partiendo de $P$ avanzáramos en la dirección que forma $\pi/6$ radianes con el eje $0X$ positivo. ¿Cuál es la pendiente de $C$ en el punto $P$? Escribe el vector tangente a $C$ en $P$ y las ecuaciones paramétricas de la recta tangente a $C$ en $P$.
- Repite el apartado anterior, ahora con el ángulo $\pi/4$ radianes.
- Idem para el ángulo $\pi/3$ radianes.
Resolución del primer apartado
Paso 1
Determinemos en primer lugar el gradiente. Para encontrar las derivadas parciales de $z$, no hace falta despejar la variable $z$; puedes derivar implícitamente. Al derivar $x^2+y^2+z^2=4$ respecto de $x$ resulta
$$2x+2zz'_x=4$$
Ninguna de las dos opciones es correcta.
$$2x+2zz'_x=0$$
No es correcto; ¿cuál es la derivada de 4?
Míralo bien; hay una correcta.
En efecto, derivando $x^2+y^2+z^2=4$ respecto de $x$,
$$2x+2zz'_x=0\hspace{.4cm} \Rightarrow \hspace{.4cm} z'_x=\frac{-x}{z}\hspace{.4cm} \Rightarrow \hspace{.4cm} z'_x(1,-1)=\frac{-1}{\sqrt{2}}$$
Igualmente, derivando respecto de $y$,
$$2y+2zz'_y=0\hspace{.4cm} \Rightarrow \hspace{.4cm} z'_y=\frac{-y}{z}\hspace{.4cm} \Rightarrow \hspace{.4cm} z'_y(1,-1)=\frac{1}{\sqrt{2}}$$
Paso 2
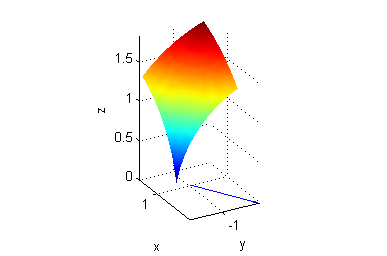
Ahora dibujamos una parte de la superficie, el punto $P$, la curva de nivel y el gradiente en $(1,-1)$:
[X,Y]=meshgrid(.6:.05:1.4,-1.4:.05:-.6); % malla de puntos para dibujar la superficie Z=sqrt(4-X.^2-Y.^2); % valor de la función sobre los puntos de la malla surf(X,Y,Z) % dibujo de la superficie shading interp hold on plot3(1,-1,sqrt(2),'*') % dibujo del punto P plot3(1,-1,0,'o') % dibujo de la proyección de P en el 'suelo': (1,-1) contour(X,Y,Z,sqrt(2)) % curva de contorno correspondiente a P quiver(1,-1,-1/sqrt(2),1/sqrt(2)) % vector gradiente en (1,-1) hold off
Resolución del segundo apartado
El plano tangente contiene a todos los puntos $(x,y,z)$ que cumplan que el vector $(x-1,y+1,z-\sqrt{2})$ sea perpendicular al vector $(f'_x(1,-1),f'_y(1,-1),-1)$. Por tanto, en este caso es
$$x-y-\sqrt{2}z=4$$
Ninguna de las dos opciones propuestas es correcta.
$$x-y+\sqrt{2}z=4$$
No es correcto; comprueba los signos.
Sí hay una correcta.
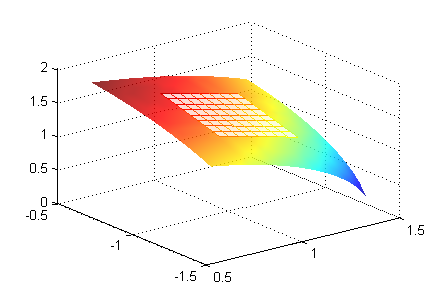
En efecto, esa es una expresión para el plano tangente. Si queremos dibujar la misma porción de superficie que antes y añadirle ahora una parte del plano tangente a $P$, escribimos
[X,Y]=meshgrid(.6:.05:1.4,-1.4:.05:-.6); % malla para la superficie Z=sqrt(4-X.^2-Y.^2); % valores de z sobre la malla anterior surf(X,Y,Z) % trazado de la superficie shading interp hold on [X,Y]=meshgrid(.8:.05:1.2,-1.2:.05:-.8); % malla para el plano tangente mesh(X,Y,(4-X+Y)/sqrt(2)) % trazado del plano plot3(1,-1,sqrt(2),'*') % punto P alpha(.8) hold off
Resolución del tercer apartado
En primer lugar hemos de buscar la dirección que forma $\pi/6$ radianes con el eje $0X$ positivo. Hazlo tú y pulsa en 'Ver'.
Ver
En efecto, sabemos que la dirección que se impone aquí es
$${\bf u}=(\frac{\sqrt{3}}{2},\frac{1}{2})$$
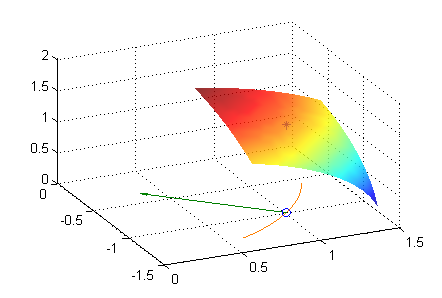
En la figura vemos la misma porción de superficie que antes, pero ahora se ha dado la misma escala en todos los ejes, para poder apreciar mejor que el ángulo que forma el vector azul, ${\bf u}$, con el eje $0X$ positivo es $\pi/6$ radianes.
La curva $C$ es la intersección de la superficie $S$ con el plano vertical que contiene a ese vector azul:
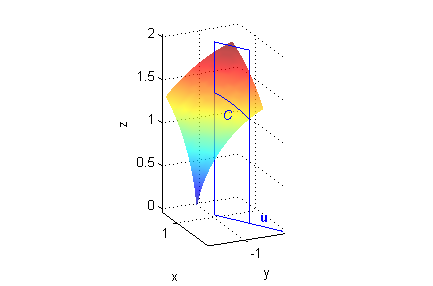

La curva $C$ es la intersección de la superficie $S$ con el plano vertical que contiene a ese vector azul:

Por la construcción de la derivada direccional , sabemos que la pendiente de la recta tangente a la curva $C$ en el punto $P(1,-1,\sqrt{2})$ es el valor de la derivada direccional de $z$ en $(1,-1)$ respecto de la dirección ${\bf u}=(\frac{\sqrt{3}}{2},\frac{1}{2})$. Recordamos también que esa derivada direccional podemos calcularla utilizando el gradiente. Hállala y pulsa en 'Ver'.
Ver
La pendiente de la curva $C$ en $P$ es
$$D_{\bf u}z(1,-1)=(z'_x(1,-1),z'_y(1,-1))\cdot {\bf u}=
(\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}})\cdot (\frac{\sqrt{3}}{2},\frac{1}{2})=\frac{1-\sqrt{3}}{2\sqrt{2}}$$
Con esta pendiente calculada, sabemos que el vector tangente a la curva $C$ en el punto $P$ es
$$(\frac{\sqrt{3}}{2},\frac{1}{2},\frac{1-\sqrt{3}}{2\sqrt{2}})$$
y unas ecuaciones paramétricas para la recta tangente a $C$ en $P(1,-1,\sqrt{2})$ son
$$\left\{\begin{array}{ll} x=1+\sqrt{3} t & \\
y=-1+t & t\in{\bf R}\\
z=\sqrt{2} + \frac{1-\sqrt{3}}{\sqrt{2}} t &
\end{array}\right.$$
Resolución del cuarto apartado
Este apartado es idéntico al anterior, sólo hemos de modificar la dirección: ahora $C$ es la curva intersección de $S$ con el plano vertical que contiene a $P$ y forma $\pi/4$ radianes con el eje $0X$ positivo: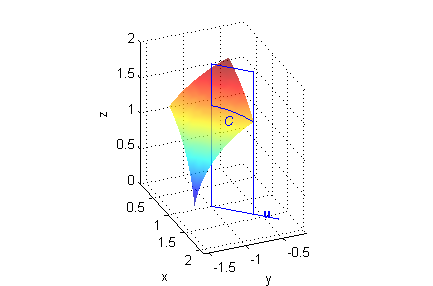
Encuentra la dirección, el vector tangente a la curva y las ecuaciones paramétricas de la recta tangente y pulsa en 'Ver'.
Ver
La dirección es
$${\bf u}=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$$
La pendiente de la curva es
$$D_{\bf u}z(1,-1)=(z'_x(1,-1),z'_y(1,-1))\cdot {\bf u}=
(\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}})\cdot (\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})=0$$
El vector tangente a la curva en $P$ es
$$(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2},0)$$
y unas paramétricas para la recta tangente a esta curva en $P$ son
$$\left\{\begin{array}{ll} x=1+ t & \\
y=-1+t & t\in{\bf R}\\
z=\sqrt{2} &
\end{array}\right.$$
Resolución del quinto apartado
Repetimos lo anterior, ahora para la dirección que forma $\pi/3$ radianes con el eje $0X$ positivo: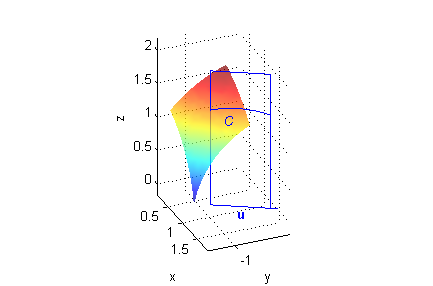
Resuelve las preguntas en este caso y pulsa en 'Ver'.
Ver
La dirección es
$${\bf u}=(\frac{1}{2},\frac{\sqrt{3}}{2})$$
La pendiente de la curva es
$$D_{\bf u}z(1,-1)=(z'_x(1,-1),z'_y(1,-1))\cdot {\bf u}=
(\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}})\cdot (\frac{1}{2},\frac{\sqrt{3}}{2})=\frac{\sqrt{3}-1}{2\sqrt{2}}$$
El vector tangente a la curva en $P$ es
$$(\frac{1}{2},\frac{\sqrt{3}}{2},\frac{\sqrt{3}-1}{2\sqrt{2}})$$
y unas paramétricas para la recta tangente a esta curva en $P$ son
$$\left\{\begin{array}{ll} x=1+ t & \\
y=-1+ \sqrt{3} t & t\in{\bf R}\\
z=\sqrt{2} +\frac{\sqrt{3}-1}{\sqrt{2}} t &
\end{array}\right.$$
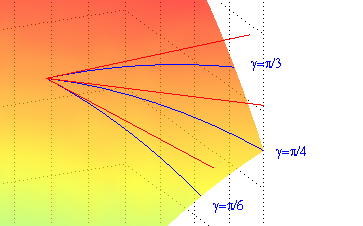
En la siguiente figura puedes ver juntos los tres arcos con los que has trabajado y un segmento de sus respectivas rectas tangentes: