Enunciado
Dada la función $f\left( {x,y} \right) = 1/xy$, se pide determinar los puntos de la gráfica de $f$ más cercanos al origen.
Representación de la función
Las curvas de nivel de esta función son hipérbolas, son curvas de la forma
$$1/xy = k \,\,\,\,\,\,\,ó\,\,\,\,\,\,\, xy =1/k $$
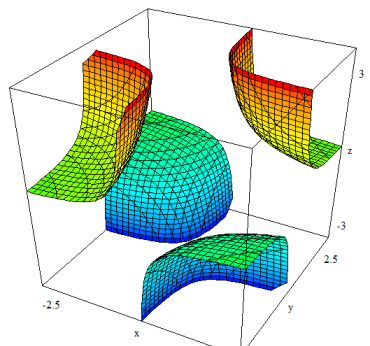
- Si k>0 entonces los puntos $\left( {x,y} \right)$ están en el primer y tercer cuadrante.
- Si k<0, los puntos $\left( {x,y} \right)$ están en el segundo y cuarto cuadrante.

Calculamos la función a optimizar
Si el punto $\left( {x,y,\,z} \right)$ es un punto de la gráfica de $f$, será de la forma $\left( {x,y,\,{1 \over {xy}}} \right)$.La función distancia de un punto de la gráfica al origen será: $$d\left( {\left( {x,y,\,{1 \over {xy}}} \right),\,\,\left( {0,0,0} \right)} \right) = \sqrt {{x^2} + {y^2} + {1 \over {{x^2}{y^2}}}} $$ Como la función distancia es positiva, minimizar la función $d$ o ${d^2}$ es equivalente. Por tanto, consideraremos como función a minimizar $${d^2}\left( {x,y} \right) = F\left( {x,y} \right) = {x^2} + {y^2} + {1 \over {{x^2}{y^2}}}$$ .
Calculamos los puntos críticos
Esta función es diferenciable, los puntos críticos son los que satisfacen:
$F_x^' = 2x - {2 \over {{x^3}{y^2}}} = 0\,\,\,\,\,\,\,\,\,\,\,\,F_y^' = 2y - {2 \over {{y^3}{x^2}}} = 0$
$x=y=0$
$x=-y$
En efecto, los puntos críticos son los que cumplen que el plano tangente es horizontal. En el conjunto de puntos que verifican estas dos ecuaciones debemos buscar los extremos de $f$ (ver condición).
Resuelve el sistema anterior y, en cuanto lo tengas, pulsa sobre el botón .
Resuelve el sistema anterior y, en cuanto lo tengas, pulsa sobre el botón .
Falso, en este punto la función no está definida, por lo tanto no tiene sentido esta opción.
Falso, en los puntos $x=-y$ el plano tangente no es horizontal.
Calculamos los puntos críticos resolviendo el sistema.
$$\left. \matrix{{x^4}{y^2} - 1 = 0 \cr {x^2}{y^4} - 1 = 0 \cr} \right\}$$
Realiza los cálculos y, en cuanto lo tengas, pulsa sobre el botón .
Realiza los cálculos y, en cuanto lo tengas, pulsa sobre el botón .
Despejando $y^2$ en la primera ecuación y sustituyendo en la segunda.
$$\left. \matrix{ {y^2} = 1/{x^4} \cr {x^6} - 1 = 0 \cr} \right\} \,\,\,\,\, \Rightarrow \,\,x = \pm 1,\,\,y = \pm 1$$
Los puntos críticos son entonces: $\left( {1,\, 1} \right)$, $\left( {1,\, -1} \right)$, $\left( {-1,\, 1} \right)$ y $\left( {-1,\, -1} \right)$.
Calcula ahora en esos puntos las derivadas parciales segundas y el hessiano. Pulsa en el botón en cuanto lo tengas.
Calcula ahora en esos puntos las derivadas parciales segundas y el hessiano. Pulsa en el botón en cuanto lo tengas.
Los valores de las derivadas parciales segundas son:
$$F_{xx}^{''} = 2 + {6 \over {{x^4}{y^2}}}, \,\,\,\,\,\,F_{yy}^{''} = 2 + {6 \over {{x^2}{y^4}}}, \,\,\,\,\,\,F_{xy}^{''} = {4 \over {{x^3}{y^3}}}$$
y el hessiano en los puntos críticos es:
$$H\left( {1,1} \right) = H\left( { - 1, - 1} \right) = \left| {\matrix{ 8 & 4 \cr 4 & {8\,} \cr } } \right|$$
$$H\left( {1, - 1} \right) = H\left( { - 1,1} \right) = \left| {\matrix{ 8 & { - 4} \cr { - 4} & {8\,} \cr } } \right|$$
Por ello, podemos concluir que los puntos:
Por ello, podemos concluir que los puntos:
son todos mínimos
son todos máximos
que tienen las componentes con igual signo son mínimos
En efecto, ya que $H > 0$ y $F_{xx}^{''}> 0$ (ver el teorema del hessiano).
Conclusión: Todos los puntos críticos son mínimos relativos de valor $\sqrt 3 $.
Conclusión: Todos los puntos críticos son mínimos relativos de valor $\sqrt 3 $.
Falso, revisa el teorema del hessiano.
Falso, revisa el teorema del hessiano.
Verificamos el resultado
En el siguiente applet puedes elegir un valor de $k>0$ para representar las curvas de nivel de la función $f\left( {x,y} \right) = 1/xy$ correspondientes al valor $k$ y $-k$.El punto $P$ está sobre la curva $f\left( {x,y} \right) = 1/xy=k$ y el punto $Q$ sobre $f\left( {x,y} \right) = 1/xy=-k$.
Estos puntos puedes moverlos arrastrándolos sobre las curvas a las que pertenecen.
Puedes comprobar que los puntos de la gráfica (P, f(P)) y (Q, F(Q)) distan siempre más del origen que los puntos de la gráfica (A, f(A)), (B, f(B)), (C,f(C)) y (D, f(D)) cuya distancia al origen es $\sqrt 3 \approx 1.7321$.