Enunciado
Dada la función $z = f\left( {x,y} \right) = {x^2} + {y^2} - 2x + 4y + 6$, se pide:
- Representar la función y las curvas de nivel.
- Calcular los extremos de la función en su dominio.
Resolución del primer apartado
Completando cuadrados en la expresión de la función $f$ tendremos que:
$$z = f\left( {x,y} \right) = {\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + 1$$
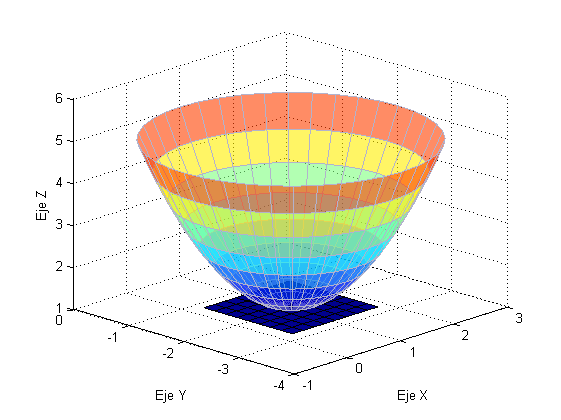
Esto significa que la gráfica de esta función es un paraboloide de vértice el punto (1, -2).
Las curvas de nivel serán las curvas $f\left( {x,y} \right) =k$ para valores de $k$ mayores o iguales a 1. Si $k>1$ estas curvas son circunferencias centradas en el punto (1, -2), si $k=1$ será el punto (0,0).
Para dibujar con Matlab la gráfica de la función y sus curvas de nivel pondremos: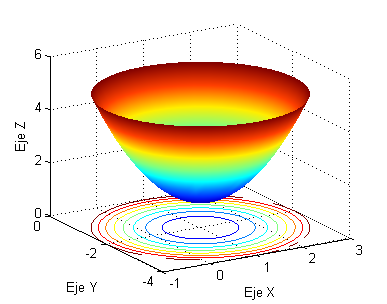
Las curvas de nivel serán las curvas $f\left( {x,y} \right) =k$ para valores de $k$ mayores o iguales a 1. Si $k>1$ estas curvas son circunferencias centradas en el punto (1, -2), si $k=1$ será el punto (0,0).
Para dibujar con Matlab la gráfica de la función y sus curvas de nivel pondremos:
a=1;b=-2; [R, P]=meshgrid(0:0.2:2,0:pi/20:2*pi); X1=a+R.*cos(P); Y1=b+R.*sin(P); Z1=X1.^2+Y1.^2-2*X1+4*Y1+6; surfc(X1,Y1,Z1); shading interp

Resolución del segundo apartado
Teniendo en cuenta la representación gráfica de la función es claro que el valor mínimo de $f$ se alcanza en el punto $\left( {1, - 2} \right)$ y que no tiene máximo.Resolvemos ahora el ejercicio suponiendo que no se conoce la gráfica de la función.
Al ser la función diferenciable sólo tiene valores extremos en los puntos en los que el plano tangente es horizontal. Por eso se calculan los puntos que cumplen:
$$f_x^' = 2x - 2 = 0 \,\,\,\,\,\, f_y^' = 2y + 4 = 0$$
$$z = {x^2} + {y^2} - 2x + 4y + 6 = 0$$
$\nabla F\left( {x,y,z} \right) = 0$, siendo $F\left( {x,y,z} \right) = {x^2} + {y^2} - 2x + 4y + 6 - z$
En efecto, el plano tangente es cero cuando $f_x^' = 2x - 2 = 0$, $f_y^' = 2y + 4 = 0$, es decir, cuando $\nabla f\left( {x,y} \right) = 0$. En el conjunto de puntos que verifican estas dos igualdades debemos buscar los extremos de $f$ (ver condición).
Resuelve el sistema y pulsa sobre el botón .

Resuelve el sistema y pulsa sobre el botón .
Falso, estos puntos serían los que estarían en la curva de nivel $f\left( {x,y} \right) = 0$. En el caso de nuestra función no hay ningún punto verificando esta igualdad ya que el conjunto imagen de $f$ es $\left[ {1,\,\infty } \right)$.
Falso, la función $F$ es $f\left( {x,y} \right) - z$ y no permite obtener los puntos críticos de la función $f$.
El punto crítico es $x = 1$, $y = - 2$.
Para analizar el tipo de extremo calculamos las derivadas de orden 2 y el hessiano en este punto.
Pulsa en el botón en cuanto lo tengas.
Para analizar el tipo de extremo calculamos las derivadas de orden 2 y el hessiano en este punto.
Pulsa en el botón en cuanto lo tengas.
Los valores de las derivadas parciales segundas y el hessiano en el punto $\left( {1, - 2} \right)$ son:
$$f_{xx}^{''} = 2, \,\,\,\,\,\,\,\,\, f_{yy}^{''} = 2,\,\,\,\,\,\,\,\,\, f_{xy}^{''} = 0, \,\,\,\,\,\,\,\,\, H\left( {1, - 2} \right) = \left| {\matrix{ 2 & 0 \cr 0 & {2\,} \cr } } \right| = 4$$
Por ello, podemos concluir que el punto $\left( {1, - 2} \right)$ es un:
Por ello, podemos concluir que el punto $\left( {1, - 2} \right)$ es un:
mínimo relativo
máximo relativo
punto de silla
ya que $H > 0, \,\,\,\,\, f_{xx}^{''} > 0$ (ver el teorema del hessiano).
Conclusión: El punto $\left( {1, - 2} \right)$ es un mínimo relativo de valor $f\left( {1, - 2} \right) = 1$.
Conclusión: El punto $\left( {1, - 2} \right)$ es un mínimo relativo de valor $f\left( {1, - 2} \right) = 1$.
Falso, revisa el teorema del hessiano.
Falso, revisa el teorema del hessiano.