Respecto de una variable independiente

Sea $z=f(x,y)$ una función diferenciable en un dominio $D$, siendo cada una de las variables $x$ e $y$ funciones de la variable $t$: $$x=x(t)\ ,\ \ y=y(t)$$ cumpliendo que existen las derivadas $x'(t)$, $y'(t)$; entonces la función $z=f(x(t),y(t))$ es derivable y se cumple que $$\frac{dz}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}$$

Para recordar más fácilmente esta fórmula podemos tener en cuenta el siguiente gráfico de dependencia siguiente:

Respecto de dos variables independientes

Sea $z=f(x,y)$ una función diferenciable en un dominio $D$, siendo cada una de las variables $x$ e $y$ funciones de otras variables $u$ y $v$: $$x=x(u,v)\ ,\ \ y=y(u,v)$$ cumpliendo que existen las derivadas parciales $x'_u$, $x'_v$, $y'_u$, $y'_v$; entonces la función $z=f(x(u,v),y(u,v))$ admite derivadas parciales y se cumple que $$z'_u=z'_xx'_u+z'_yy'_u \ \ ,\ \ z'_v=z'_xx'_v+z'_yy'_v$$

En este caso el gráfico de dependencia es:

Implícita respecto de una variable independiente

TEOREMA de la función implícita: La ecuación $F(x,y)=0$ define en un entorno del punto $P(a,b)$ a la variable $y$ como función implícita de $x$, es decir $y=f(x)$, si $F(a,b)=0$, las derivadas parciales $F'_x(x,y)$ y $F'_y(x,y)$ son continuas en un entorno de $P(a,b)$ y $F'_y(a,b)\neq 0$

TEOREMA sobre la derivación implícita: Si la ecuación $F(x,y)=0$ define en un entorno del punto $P(a,b)$ a la variable $y$ como función implícita de $x$, siendo $F'_y(a,b)\neq 0$, entonces $$\frac{dy}{dx}(a)=-\frac{F'_x(a,b)}{F'_y(a,b)}$$

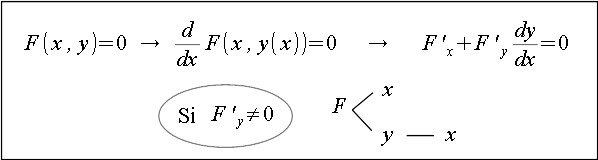
Obviamente este teorema se puede escribir intercambiando los papeles de $x$ y de $y$:

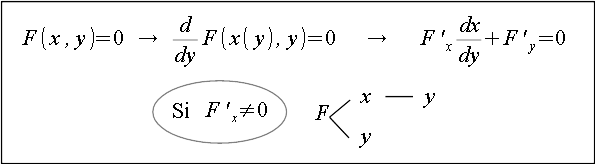
Implícita respecto de dos variables independientes

TEOREMA de la función implícita: La ecuación $F(x,y,z)=0$ define en un entorno del punto $P(a,b,c)$ a la variable $z$ como función implícita de $x$ e $y$, es decir $z=f(x,y)$, si $F(a,b,c)=0$, las derivadas parciales $F'_x(x,y,z)$, $F'_y(x,y,z)$ y $F'_z(x,y,z)$ son continuas en un entorno de $P(a,b,c)$ y $F'_z(a,b,c)\neq 0$.

TEOREMA sobre la derivación implícita: Si la ecuación $F(x,y,z)=0$ define en un entorno del punto $P(a,b,c)$ a la variable $z$ como función implícita de $x$ e $y$, siendo $F'_z(a,b,c)\neq 0$, entoncees $$\frac{\partial z}{\partial x}(a,b)=-\frac{F'_x(a,b,c)}{F'_z(a,b,c)}\ \ \ , \ \ \ \frac{\partial z}{\partial y}(a,b)=-\frac{F'_y(a,b,c)}{F'_z(a,b,c)}$$.