Enunciado
Considera la función $$f(x)=\frac{1}{\sqrt[4]{2x^2+1}}$$
- Desarrolla $f(x)$ en serie de potencias de $x$.
- Encuentra el campo de convergencia de la serie obtenida.
- Calcula una cota superior del error cometido cuando se toma como suma de la serie convergente la suma de los tres primeros términos.
- ¿Cuál es la cota de error en la aproximación descrita en el apartado anterior del siguiente valor?
$$\frac{1}{\sqrt[4]{2.28}}$$
Resolución primer apartado
Para encontrar ese desarrollo,
Encontramos la función derivada $n$_ésima de $f(x)$.
Utilizaremos la geométrica: $\frac{1}{\sqrt[4]{2x^2+1}}=\frac{1}{(1-(-2x^2))^{1/4}}=
\sum_{n=0}^\infty (-2x^2)^{n/4}$
Una de las propuestas es incorrecta y la otra es inviable.
Más que incorrecto es inviable.
La segunda igualdad es una barbaridad, la raíz de la suma no es la suma de las raíces. Lo correcto sería
$$\frac{1}{\sqrt[4]{2x^2+1}}=\frac{1}{(1-(-2x^2))^{1/4}}=
\left(\sum_{n=0}^\infty (-2x^2)^{n}\right)^{1/4}$$
pero ¿cómo haríamos después la raíz de un sumatorio?
En efecto, así que hay que pensar en otros métodos.
Para encontrar este desarrollo lo más apropiado es utilizar la generalización del desarrollo de un binomio. También podríamos encontrar las derivadas sucesivas en el cero, a partir de una fórmula de recurrencia obtenida con la fórmula de Leibniz; este segundo método resulta más complicado en este caso, así que nos quedamos con la generalización del desarrollo del binomio .
Paso 1
Aplicada a este caso, resulta ...
Ninguna de las propuestas es correcta
$$f(x)=\frac{1}{\sqrt[4]{2x^2+1}}=1+\sum_{n=1}^\infty \left(\begin{array}{c} -1/4 \\ n\end{array}\right) 2^nx^n\ \ \ \mbox{en} \ \ \ |x|< 1$$
$$f(x)=\frac{1}{\sqrt[4]{2x^2+1}}=1+\sum_{n=1}^\infty \left(\begin{array}{c} -1/4 \\ n\end{array}\right) 2^nx^{2n}\ \ \ \mbox{en} \ \ \ |x|< \frac{1}{2}$$
$$f(x)=\frac{1}{\sqrt[4]{2x^2+1}}=1+\sum_{n=1}^\infty \left(\begin{array}{c} -1/4 \\ n\end{array}\right) 2^nx^{2n}\ \ \ \mbox{en} \ \ \ |x|< \frac{1}{\sqrt{2}}$$
Hay una correcta.
No es correcta: hemos de aplicar la fórmula a $(2x^2)^n$
Es correcta la expresión de la serie, pero no el intervalo de convergencia: estamos aplicando la fórmula a $(2x^2)^n$
Esa es la correcta. Detrás de la serie aparece el intervalo de convergencia. De momento no conocemos el campo de convergencia.
Paso 2
Ahora hemos de escribir el coeficiente $\left(\begin{array}{c} -1/4 \\ n\end{array}\right)$ de forma menos esquemática, utilizando productos de números. Inténtalo y pulsa en 'Ver'. Recuerda que la fórmula de ese coeficiente la tienes en la ventana generalización del desarrollo del binomio
Ver
$$\left(\begin{array}{c} -1/4 \\ n\end{array}\right)=\frac{1}{n!}\left(\frac{-1}{4}\right)\left(\frac{-1}{4}-1\right)\left(\frac{-1}{4}-2\right)\ldots \left(\frac{-1}{4}-n+1\right)=$$
$$=\frac{(-1)^n}{n!}\frac{1\cdot5\cdot 7\cdots (4n-3)}{4^n}$$
Este coeficiente va multiplicado por $2^n$, con lo que resultará
$$f(x)=\frac{1}{\sqrt[4]{2x^2+1}}=1+\sum_{n=1}^\infty \frac{(-1)^n\cdot 1\cdot5\cdot 7\cdots (4n-3)}{2^n n!}x^{2n} \ \ \ \mbox{en} \ \ \ |x|< \frac{1}{\sqrt{2}}$$
En la figura puedes ver las gráficas en $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ de las sumas parciales $S_1(x)$ a $S_5(x)$; realmente también está la primera, $S_0(x)=1$, que puede no distinguirse por coincidir con el marco; observamos que estas gráficas se van acercando a la gráfica de la función (en gris oscuro) alternativamente por arriba y por abajo:
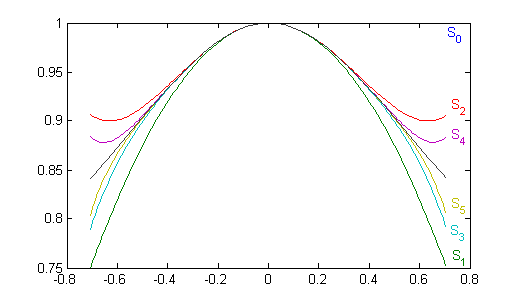

f=@(x,n) ((-1)^n*prod(1:4:4*n-3))/(2^n*factorial(n))*x.^(2*n); x=-1/sqrt(2):.01:1/sqrt(2); s(1,:)=ones(size(x)); for k=2:6 s(k,:)=s(k-1,:)+f(x,k-1); end s(7,:)=1./(2*x.^2+1).^(1/4); plot(x,s) clear all
Resolución segundo apartado
Ya conocemos el intervalo de convergencia, así que lo que nos queda es estudiar la convergencia de $$1+\sum_{n=1}^\infty \frac{(-1)^n\cdot 1\cdot5\cdot 7\cdots (4n-3)}{2^n n!}x^{2n}$$ en los extremos de este intervalo: $$(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$$ Puesto que en la serie sólo hay potencias de grado par, la serie resultante en $x=-\frac{1}{\sqrt{2}}$ es la misma que la resultante en $x=\frac{1}{\sqrt{2}}$. Encuentra esa serie numérica y pulsa en 'Ver'.
Ver
Puesto que $$\left(\frac{\pm 1}{\sqrt{2}}\right)^{2n}=\frac{1}{2^n}$$
la serie resulta $$1+\sum_{n=1}^\infty \frac{(-1)^n\cdot 1\cdot5\cdot 7\cdots (4n-3)}{4^n n!}$$
que es una serie alternada.
Para analizar su convergencia
Utilizamos el criterio del cociente
Ninguna de las dos opciones presentadas es correcta
Utilizamos el criterio de Leibniz
No es correcta: el criterio del cociente sólo puede utilizarse sobre series de términos del mismo signo.
No, pues sí puede utilizarse el criterio de Leibniz
Esto es lo correcto. La convergencia de esta serie puede analizarse con el criterio de Leibniz, puesto que
$$a_n=\left|\frac{(-1)^n\cdot 1\cdot5\cdot 7\cdots (4n-3)}{4^n n!}\right|=\frac{1\cdot5\cdot 7\cdots (4n-3)}{4^n n!}$$
es un infinitésimo decreciente (se cumplen por tanto las condiciones suficientes que establece el criterio de Leibniz para la convergencia de una serie alternada).
Resolución tercer apartado
La suma de los primeros tres términos es la suma parcial $S_2(x)$: $$S_2(x)=1+\sum_{n=1}^2 \frac{(-1)^n\cdot 1\cdot5\cdot 7\cdots (4n-3)}{2^n n!}x^{2n}= 1-\frac{x^2}{2}+\frac{5x^4}{8}$$ Observamos que para cualquier valor de $x$ en que se tome la serie, ésta resultará una serie numérica alternada, ya que en cada sumando la $x$ va elevada al cuadrado. Así, podemos aplicar que el error cometido está acotado por el primer término despreciado: $$|f(x)-S_2(x)|< |a_3x^6|=\frac{5\cdot 9}{2^3\cdot 3!}x^6=\frac{15}{16}x^6$$ En la figura de la izquierda están las gráficas de $S_2(x)$ (azul) y $f(x)$ (verde) en $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$; a la derecha está la gráfica de la cota $\frac{15}{16}x^6$, en la que podemos observar cómo crece esta cota de error según nos alejamos de $x=0$: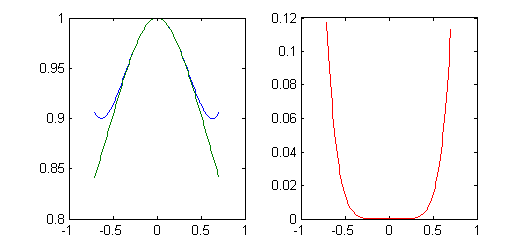
f=@(x,n) ((-1)^n*prod(1:4:4*n-3))/(2^n*factorial(n))*x.^(2*n); x=-1/sqrt(2):.01:1/sqrt(2); s(1,:)=ones(size(x))+f(x,1)+f(x,2); s(2,:)=1./(2*x.^2+1).^(1/4); subplot(1,2,1) plot(x,s) subplot(1,2,2) plot(x,15*x.^6/16,'r') clear all
Resolución cuarto apartado
Para aproximar $$\frac{1}{\sqrt[4]{2.28}}$$ utilizando el desarrollo de $$f(x)=\frac{1}{\sqrt[4]{2x^2+1}}$$ hemos de determinar el valor de $x$ para el cual $2x^2+1=2.28$. Hazlo y pulsa en 'Ver'.
Ver
$$2x^2+1=2.28 \ \ \ \Rightarrow\ \ \ x=\pm .8$$
Entonces, utilizando los apartados anteriores
$$|f(.8)-S_2(.8)|< |a_3.8^6|=\frac{5\cdot 9}{2^3\cdot 3!}.8^6$$
La otra propuesta no es correcta
No es correcto, pues $\pm.8$ no están en el campo de convergencia de la serie, ya que
$$.8=\frac{4}{5}> \frac{1}{\sqrt{2}}$$
luego no podemos utilizar ese desarrollo para aproximar el valor de la función en ese punto.
En efecto, la propuesta no es correcta, pues $\pm.8$ no están en el campo de convergencia de la serie, luego no podemos utilizar ese desarrollo para aproximar el valor de la función en ese punto.