Elevar una serie al cuadrado puede ser muy complicado si queremos llegar al término general. Lo mismo ocurre con la multimplicación de series. Ese método hay que verlo como último recurso, si no hay más opciones. Elige de nuevo

Efectivamente, lo mejor en este caso es utilizar que $$\mbox{Ch}\, x=\frac{e^x+e^{-x}}{2}\ \ \ ,\ \ \ \mbox{Sh}\, x=\frac{e^x-e^{-x}}{2}$$ Escribe $f(x)$ en terminos de la exponencial y pulsa en 'Continuar'.
Continuar

No, ya que $$e^u=\sum_{n=0}^\infty \frac{u^n}{n!}$$ Elige de nuevo

No, ya que $$e^u=\sum_{n=0}^\infty \frac{u^n}{n!}$$ Elige de nuevo

No, ya que debemos cambiar $u$ por $4x$ en $$e^u=\sum_{n=0}^\infty \frac{u^n}{n!}$$ Elige de nuevo

En efecto ese es el desarrollo correcto. Análogamente, $$e^{-4x}=\sum_{n=0}^\infty \frac{(-4x)^n}{n!}$$ Estos desarrollos son válidos en todos los reales (radio de convergencia infinito), pues así lo es el desarrollo de la exponencial Continuar

La suma resulta $$e^{4x}+e^{-4x}=\sum_{n=0}^\infty \frac{(4x)^n}{n!}+\sum_{n=0}^\infty (-1)^n\frac{(4x)^n}{n!}= \sum_{n=0}^\infty [1+(-1)^n]\frac{(4x)^n}{n!}$$ En este sumatorio son nulos todos los términos de grado impar; el coeficiente correspondiente a $n$ par será $$2\frac{(4x)^n}{n!}$$ de manera que podemos escribir $$e^{4x}+e^{-4x}=2\sum_{n=0}^\infty \frac{(4x)^{2n}}{(2n)!}$$ Por tanto, $$f(x)=\mbox{Ch}^2\, x\,\mbox{Sh}^2\, x=\frac{-1}{8}+\frac{1}{8}\sum_{n=0}^\infty \frac{(4x)^{2n}}{(2n)!}= \frac{-1}{8}+\frac{1}{8}+\sum_{n=1}^\infty \frac{(4x)^{2n}}{(2n)!}=\sum_{n=1}^\infty \frac{(4x)^{2n}}{(2n)!}\ \ \ , \ \ x\in{\bf R}$$ Observa que la función $f(x)$ es par y su gráfica pasa por el origen. Continuar

Una opción es escribir,

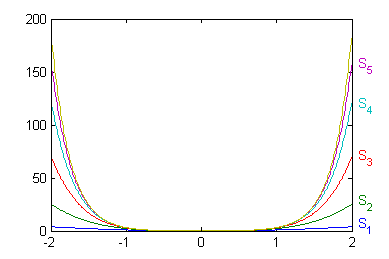
f=@(x,n) (4*x).^(2*n)/(8*factorial(2*n));
x=-2:.01:2;
s(1,:)=f(x,1);
for k=2:5
s(k,:)=s(k-1,:)+f(x,k);
end
s(6,:)=cosh(x).^2.*sinh(x).^2;
plot(x,s)
clear

Con estas líneas obtenemos la siguiente figura, donde la gráfica amarilla es la de la función $S(x)=\mbox{Ch}^2\, x\,\mbox{Sh}^2\, x$.

Ver resumen

El desarrollo de $\frac{\mbox{sen}\, x}{x}$ es fácil de encontrar, pero no elevarlo al cuadrado Elige de nuevo

no es fácil elevar un sumatorio infinito al cuadrado Elige de nuevo

Efectivamente, es mejor conseguir el desarrollo de $(\mbox{sen}\, x)^2=\mbox{sen}^2\, x$ de otra manera. Por ejemplo, expresando $$\mbox{sen}^2\, x=\frac{1}{2}(1-\cos 2x)$$ y utilizando que $$\cos x=\sum_{n=0}^\infty (-1)^n\frac{x^{2n}}{(2n)!}\ \ \ ,\ \ \ x\in{\bf R}$$ hazlo tú y pulsa en 'Continuar'.
Continuar

$$\mbox{sen}^2\, x=\sum_{n=0}^\infty (-1)^{n}\frac{2^{2n+1}}{(2n+2)!}x^{2n+2}\ \ \ ,\ \ \ x\in{\bf R}$$ Una alternativa para encontrar este desarrollo es hacer la derivada de $\mbox{sen}^2\, x$ y escribirla como $\mbox{sen}\, 2x$: $$\frac{d}{dx}\mbox{sen}^2\, x=2\, \mbox{sen}\, x\, \cos x=\mbox{sen}\, 2x$$ Esto quiere decir que $\mbox{sen}^2\, x$ es una primitiva de $\mbox{sen}\, 2x$; todas las primitivas de $\mbox{sen}\, 2x$ son $$\int \mbox{sen}\, 2x\, dx= \sum_{n=0}^\infty \frac{(-1)^n2^{2n+1}}{(2n+1)!}\int x^{2n+1}\, dx= \sum_{n=0}^\infty (-1)^{n}\frac{2^{2n+1}}{(2n+2)!} x^{2n+2}+C\ \ \ ,\ \ \ x\in{\bf R}$$ Por tanto y puesto que $\mbox{sen}^2\, 0=0$, $$\mbox{sen}^2\, x= \sum_{n=0}^\infty (-1)^{n}\frac{2^{2n+1}}{(2n+2)!} x^{2n+2}\ \ \ ,\ \ \ x\in{\bf R}$$ Continuar

Es fácil llegar a que $$f(x)=\left(\frac{\mbox{sen}\, x}{x}\right)^2= \sum_{n=0}^\infty (-1)^{n}\frac{2^{2n+1}}{(2n+2)!} x^{2n}\ \ \ ,\ \ \ x\in{\bf R}$$ Obviamente la función $f(x)=\left(\frac{\mbox{sen}\, x}{x}\right)^2$ es par y corta al eje $0Y$ en el punto $(0,1)$. Observa que hemos podido dividir por $x^2$ todos los términos del sumatorio de $\mbox{sen}^2\, x$ y seguir teniendo una serie de potencias porque el primer sumando de ese sumatorio es el de $x^2$. Continuar

Una opción es escribir,

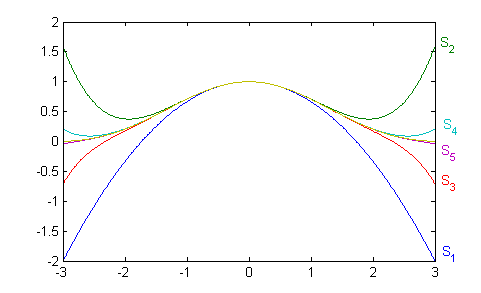
f=@(x,n) 2*(-1)^n*(2*x).^(2*n)/(factorial(2*n+2));
x=-3:.01:3;
s(1,:)=f(x,1)+1;
for k=2:5
s(k,:)=s(k-1,:)+f(x,k);
end
s(6,:)=sin(x).^2./x.^2;
plot(x,s)
clear

Con estas líneas obtenemos la siguiente figura, donde la gráfica amarilla es la de la función $S(x)$.

Ver resumen