Suma y campo de convergencia de una serie de potencias

Enunciado

Determina el campo de convergencia y la suma de la serie $$S(x)=\sum_{n=0}^\infty (\mbox{Ch}\, na)\, x^n$$ siendo $a$ cualquier número real positivo. Después toma $a=1$ y dibuja las sumas parciales $S_k(x)$ para $k=1$ hasta $k=4$, así como la función $S(x)$ en el intervalo $(-.3,.3)$.

Resolución

Sabemos que el intervalo de convergencia de una serie de potencias como ésta es siempre un intervalo centrado en el punto $x=0$.

Paso 1

Hemos de empezar encontrando el radio de convergencia de esta serie. Al estudiar la convergencia absoluta de la serie mediante el criterio del cociente llegamos al límite $$L=\lim_{n\rightarrow \infty} \left| \frac{\mbox{Ch}\, (n+1)a}{\mbox{Ch}\, na}x\right| =\lim_{n\rightarrow \infty} \frac{\mbox{Ch}\, (n+1)a}{\mbox{Ch}\, na}|x|$$ donde los valores absolutos quedan sólo en $x$ porque la función coseno hiperbólico es siempre positiva. ¿Como calculamos ese límite? Inténtalo sustituyendo el coseno hiperbólico en función de la exponencial $$\mbox{Ch}(u)=\frac{e^u+e^{-u}}{2}$$ Pulsa en 'Ver' cuando tengas el valor del límite.

Ver

En efecto, $$\frac{\mbox{Ch}\, (n+1)a}{\mbox{Ch}\, na}=\frac{e^{(n+1)a}+e^{-(n+1)a}}{e^{na}+e^{-na}}=\frac{e^{na}e^a+e^{-na}e^{-a}}{e^{na}+e^{-na}}=\frac{e^a+e^{-2na}e^{-a}}{1+e^{-2na}}$$ esta sucesión, puesto que $a$ es positivo, tiende a $e^a$ cuando $n\rightarrow \infty$. Por tanto, el límite $L$ es $$L=e^a|x|$$ La serie es absolutamente convergente cuando $$|x|<e^{-a}$$ El radio de convergencia es $R=e^{-a}$.

Paso 2

Por ser $R=e^{-a}$ el radio de convergencia, sabemos que hemos de estudiar la convergencia en los puntos $x=-e^{-a}$ y $x=e^{-a}$.

En $x=e^{-a}$ la serie es $$\sum_{n=0}^\infty (\mbox{Ch}\, na) e^{-an}$$ ¿Cómo analizamos su convergencia?

Aplicamos el criterio del cociente pues es una serie de términos positivos

Sustituimos el coseno hiperbólico en función de la exponencial y analizamos el término general

Eso no conduce a nada, pues para $x=e^{-a}$, el límite $L$ es 1, que es precisamente el caso dudoso del criterio del cociente. Eso ocurre siempre en los extremos del intervalo de convergencia.

En efecto, haciendo eso y operando, resulta $$\frac{1}{2}\sum_{n=0}^\infty (e^{na}+e^{-na})e^{-an}= \frac{1}{2}\sum_{n=0}^\infty (1+e^{-2na})$$ Podemos fácilmente ver que esta serie es divergente porque su término general no es un infinitésimo.

En $x=-e^{-a}$ la serie es $$\sum_{n=0}^\infty (\mbox{Ch}\, na) (-1)^n e^{-an}$$ Analiza la convergencia de esta serie y pulsa en 'Ver' cuando lo tengas.

Ver

La serie es $$\frac{1}{2}\sum_{n=0}^\infty (1+e^{-2na})(-1)^n e^{-an}$$ que como ocurría con la anterior, es fácil detectar que no converge pues su término general no es un infinitésimo. Se concluye por tanto que el campo de convergencia es el intervalo $(-e^{-a},e^{-a})$.

Paso 3

Para sumar la serie $$S(x)=\sum_{n=0}^\infty (\mbox{Ch}\, na)\, x^n$$ utilizamos

Derivación y posterior integración

La fórmula del binomio

Sustituir el coseno hiperbólico en función de la exponencial

Ese método no sirve aquí

En efecto, al sustituir el coseno hiperbólico en función de la exponencial, podemos escribir la serie como suma de dos: $$S(x)=\frac{1}{2}\sum_{n=0}^\infty e^{na}x^n+\frac{1}{2}\sum_{n=0}^\infty e^{-na}x^n$$ Estas dos series son convergentes en el intervalo $(-e^{-a},e^{-a})$ (puedes comprobarlo con el criterio del cociente). Por tanto hemos de sumar cada una de ellas y así obtener $S(x)$. Para sumarlas, observa que $$e^{na}x^n=(e^ax)^n\ \ \ \mbox{y} \ \ \ e^{-na}x^n=(e^{-a}x)^n$$ Sigue tú y pulsa en 'Continuar'.

En efecto, las series $$\frac{1}{2}\sum_{n=0}^\infty (e^ax)^n\ \ \ \mbox{y} \ \ \ \frac{1}{2}\sum_{n=0}^\infty (e^{-a}x)^n$$ son geométricas de razón $$e^ax\ \ \ \mbox{y} \ \ \ e^{-a}x$$ respectivamente, ambas de valor absoluto menor que 1. Teniendo en cuenta la suma de la serie geométrica , $$\frac{1}{2}\sum_{n=0}^\infty e^{na}x^n=\frac{1}{2}\frac{1}{1-e^ax} \ \ \ \ \ \mbox{y} \ \ \ \ \ \ \frac{1}{2}\sum_{n=0}^\infty e^{-na}x^n=\frac{1}{2}\frac{1}{1-e^{-a}x}$$ Sumando ambas resultará $$S(x)=\frac{1}{2}\left(\frac{1}{1-e^ax}+\frac{1}{1-e^{-a}x}\right) \ \ ,\ \ |x|<e^{-a}$$ Observa que precisamente los denominadores se anulan en $x=e^{-a}$ y $x=e^{a}$, puntos donde la función deja de ser continua y por tanto representable por una serie de potencias. Podemos dejar este resultado así o también ponerlo en una única fracción y en función del $\mbox{Ch}\, a$. Inténtalo y pulsa en 'Ver'.

Ver

$$S(x)=\frac{1}{2}\left(\frac{1}{1-e^ax}+\frac{1}{1-e^{-a}x}\right)= \frac{1}{2}\frac{2-x(e^a+e^{-a})}{(1-e^ax)(1-e^{-a}x)}=\frac{1-x\mbox{Ch}\, a}{1+x^2-2x\mbox{Ch}\, a}$$

Debemos hacer las gráficas de $$S_1(x)=\sum_{n=0}^1(\mbox{Ch}\, n)\, x^n\ \ ,\ \ S_2(x)=\sum_{n=0}^2 (\mbox{Ch}\, n)\, x^n$$ $$S_3(x)=\sum_{n=0}^3(\mbox{Ch}\, n)\, x^n \ \ ,\ \ S_4(x)=\sum_{n=0}^4 (\mbox{Ch}\, n)\, x^n \ \ ,\ \ S(x)=\frac{1-x\mbox{Ch}\, 1}{1+x^2-2x\mbox{Ch}\, 1}$$ en el intervalo $(-.3,.3)$. Primero hemos de asegurarnos que la función $S(x)$ está definida en ese intervalo, comprobando que $.3<e^{-1}$; esto lo podemos hacer simplemente calculando $e^{-1}$ en la calculadora o el ordenador. Para dibujar las gráficas utilizaremos aquí el mismo proceso del ejercicio anterior. Así, las siguientes líneas deberían dibujar esas gráficas:

f=@(x,n) cosh(n)*x.^n;
x=-.3:.01:.3;
s(1,:)=f(x,1);
for k=2:4
s(k,:)=s(k-1,:)+f(x,k);
end
s(5,:)=(1-cosh(1)*x)./(1+x.^2-2*cosh(1)*x);
plot(x,s)
clear

Es correcto

Es incorrecto

No, no es correcto, pues en este caso, la serie empieza en $n=0$, de manera que $S_1(x)$ no es $(\mbox{Ch}\, 1)\, x$ sino que $S_1(x)=1+(\mbox{Ch}\, 1)\, x$

Efectivamente no es correcto, pues en este caso, la serie empieza en $n=0$, de manera que $S_1(x)$ no es $(\mbox{Ch}\, 1)\, x$ sino que $S_1(x)=1+(\mbox{Ch}\, 1)\, x$. Así que lo correcto será:

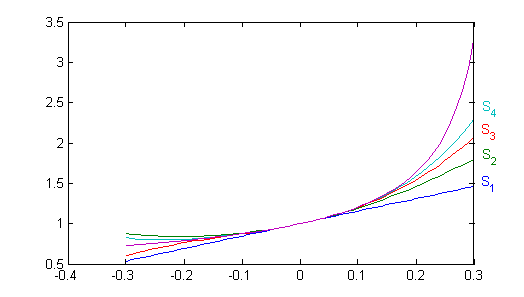
f=@(x,n) cosh(n)*x.^n;
x=-.3:.01:.3;
s(1,:)=f(x,1)+1;
for k=2:4
s(k,:)=s(k-1,:)+f(x,k);
end
s(5,:)=(1-cosh(1)*x)./(1+x.^2-2*cosh(1)*x);
plot(x,s)
clear

Resumen

encontrar el radio o el intervalo de convergencia,
estudiar la convergencia en los extremos para determinar el campo
sumar la serie utilizando la suma de geométricas
dibujar unas sumas parciales y la función suma.

Índice de tema