Índice de tema

 

Enunciado

Se considera la función $f(x)$ $\frac{\pi}{2}-$ periódica que en el intervalo $\left[-\frac{\pi}{4},\frac{\pi}{4}\right]$ se define por $$\left\{\begin{array}{lll}0 &\mbox{si} & -\frac{\pi}{4}<x<0 \\ \mbox{sen}\, x &\mbox{si} & 0<x<\frac{\pi}{4}\end{array}\right.$$
  1. Encuentra la serie de Fourier de $f(x)$ en forma compleja.
  2. Deduce de la serie anterior la serie en forma trigonométrica.
  3. Escribe una función Matlab con la que representas sumas parciales de la serie del apartado anterior en el intervalo $[\frac{-3\pi}{4},\frac{3\pi}{4}]$: la función tendrá dos variables de entrada, el índice $N$ de la última suma parcial que debe representarse y, por si no quieren representarse todas, un valor $inc$ que será el salto a tomar.

Resolución del primer apartado

Paso 1

Dibujamos la función, por ejemplo en un intervalo que abarca tres periodos: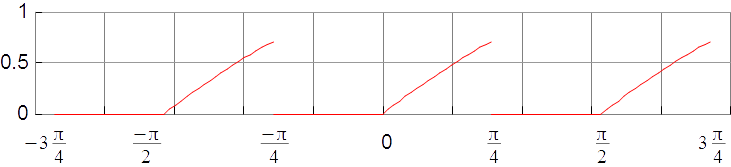

Gráfica

Puesto que se cumplen las condiciones para ser desarrollable en serie de Fourier (condiciones de Dirichlet) y $p=\frac{\pi}{4}$, el desarrollo de $f(x)$ y sus coeficientes son $$f(x)=\sum_{-\infty}^\infty c_ne^{i4n x}\ \ ,\ \ \ c_n=\frac{2}{\pi}\int_{-\pi/4}^{\pi/4} \mbox{sen}\, x\, e^{-i4n x}\, dx\ \ \ ,\ \ n\in{\bf Z}$$
Correcto
Incorrecto
No es correcto; es cierto que $$c_n=\frac{2}{\pi}\int_{-\pi/4}^{\pi/4} f(x) e^{-i4n x}\, dx$$ pero ten en cuenta que entre $-\frac{\pi}{4}$ y 0 la función se anula.
En efecto, es cierto que $$c_n=\frac{2}{\pi}\int_{-\pi/4}^{\pi/4} f(x) e^{-i4n x}\, dx$$ pero teniendo en cuenta que entre $-\frac{\pi}{4}$ y 0 la función se anula, tendremos que $$c_n=\frac{2}{\pi}\int_{0}^{\pi/4} \mbox{sen}\, x\, e^{-i4n x}\, dx\ \ \ ,\ \ n\in{\bf Z}$$

Paso 2

En este paso han de calcularse las integrales que conducen a $c_n$. Empezamos haciendo la correspondiente a $n=0$. Hazla tú y pulsa en 'Ver'.
Ver
$$c_0=\frac{2}{\pi}\int_{0}^{\pi/4} \mbox{sen}\, x \, dx=\left[-\frac{2}{\pi}\cos t\right]_{0}^{\pi/4}=\frac{1}{\pi}(2-\sqrt{2})$$
Para calcular la indefinida $I=\int\mbox{sen}\, x e^{-i4n x}\, dx$ siendo $n\neq 0$, aplicamos integración por partes dos veces. Pincha en este enlace si quieres ver los detalles. Una vez que sabemos que $$I=\int\mbox{sen}\, x e^{-i4n x}\, dx=\frac{1}{16n^2-1}\left(4ni\,\mbox{sen}\, x+\cos x\right)e^{-i4n x}+C$$ aplicamos la regla de Barrow para hallar $c_n$. Hazlo tú y pulsa en 'Ver'.
Ver
$$c_n=\frac{2}{\pi}I_0^{\pi/4}=\frac{2}{(16n^2-1)\pi}\left[\frac{\sqrt{2}}{2}(4ni+1)e^{-in\pi}-1\right]=\frac{1}{(16n^2-1)\pi}\left[\sqrt{2}(4ni+1)(-1)^n-2\right]$$ con lo cual la serie de Fourier de $f(x)$ en forma compleja es $$f(x)=\frac{1}{\pi}\left[2-\sqrt{2}+\sum_{n\in{\bf Z-\{0\}}} \frac{\sqrt{2}(4ni+1)(-1)^n-2}{16n^2-1} e^{i4n x}\right]$$

Resolución del segundo apartado

Teniendo en cuenta la relación entre los coeficientes de la forma compleja y los de la forma trigonométrica: $$a_n=2\mbox{ Re }c_n \ \ \ ,\ \ \ b_n=-2\mbox{ Im }c_n$$ tendremos que $$a_n=\frac{2}{\pi}\frac{\sqrt{2}(-1)^n-2}{16n^2-1}\ \ \ ,\ \ \ b_n=\frac{2}{\pi}\frac{4(-1)^{n+1}n}{16n^2-1}$$ con lo cual la serie de Fourier de $f(x)$ en forma trigonométrica es ... escríbela y pulsa en 'Ver'.
Ver
$$f(x)=\frac{1}{\pi}(2-\sqrt{2})+\frac{2}{\pi}\sum_{n=1}^\infty \frac{1}{16n^2-1}\left[(\sqrt{2}(-1)^n-2)\cos 4nx +4n(-1)^{n+1}\mbox{sen}\, 4nx\right]$$

Resolución del tercer apartado

Hemos de dibujar en $[\frac{-3\pi}{4},\frac{3\pi}{4}]$ la gráfica de las funciones $$S_k(x)=\frac{a_0}{2}+\sum_{n=1}^k (a_n\cos 4nx+b_n\mbox{sen}\, 4nx)$$ Hay muchas maneras de generar esas gráficas, la que se presenta aquí es sólo una opción. Piensa y escribe cada tarea que se propone y pulsa en 'Continuar'
  • Declaramos la función con sus argumentos de entrada:
function sumasparcialesFourier(N,inc)
  • Por comodidad, guardamos en una variable el semiperiodo:
    • p=pi/4;
  • Generamos un vector de abscisas en un periodo, teniendo en cuenta que entre $-\pi/4$ y 0 la función vale 0:
    • xf=[-p 0 linspace(0,p,20)];
  • Generamos un vector con los valores de las ordenadas:
    • f=[0 0 sin(xf(3:end))];
  • Dibujamos la gráfica, en rojo y un poco más gruesa, de la función en tres periodos:
    • plot([xf-2*p, xf, xf+2*p],[ f f f],'r','Linewidth',1.2)
  • Pedimos igual escala en los ejes, añadimos una malla y mantemos abierta la figura:
    • axis equal; grid on; hold on
  • Generamos un vector de abscisas para la gráfica de las sumas parciales:
    • x=linspace(-3*p,3*p);
  • Guardamos en una variable el valor del primer coeficiente:
    • c0=(2-sqrt(2))/pi;
  • Definimos una matriz de tantas filas como una unidad más que el último índice que se vaya a acumular en la suma parcial y tantas columnas como la longitud del vector de abscisas; inicialmente todas las celdas de esta matriz guardan el valor del primer sumando de la serie:
    • y=c0*ones(N+1,length(x));
  • Comienza un ciclo que va calculando cada sumando y acumulándolo a los anteriores: iniciamos el ciclo
    • for k=1:N
  • Definimos el coeficiente complejo:
    • ck=((-1)^k*(1+4*k*i)*sqrt(2)-2)/((16*k^2-1)*pi);
  • Definimos el sumando correspondiente a este coeficiente:
    • tk=2*real(ck)*cos(4*k*x)-2*imag(ck)*sin(4*k*x);
  • Acumulamos este sumando a la suma de los anteriores y cerramos el ciclo:
    • y(k+1,:)=y(k,:)+tk;
end
  • Dibujamos las columnas de la matriz frente al vector de abscisas; se comienza por la suma parcial con dos términos:
    • plot(x,y(2:inc:N,:))
  • Dibujamos la última suma parcial en negro, cerramos la figura y la función:
    •  plot(x,y(N+1,:),'k','Linewidth',1.2);
hold off
end
    Cuando en la ventana de comandos ejecutamos 
     sumasparcialesFourier(20,6)
    obtenemos las gráficas de la siguiente figura (las etiquetas del eje horizontal se han modificado después)

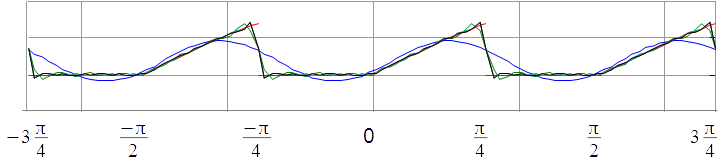
    Gráfica


    Se incluye a continuación todo el código, añadiendo algunas líneas de comentario: 
    function sumasparcialesFourier(N,inc)
% Esta función dibuja en rojo la función que vale sen(t) para t entre 0 y pi/4 y vale
% cero entre -pi/4 y 0 y que se repite periódicamente
% con periodo T=pi/2. Dibuja después las N+1 primeras sumas
% parciales del desarrollo de Fourier de esta función
% periódica, si inc=1; si no, va saltando ese incremento.
%  La última dibuja remarcada en negro.
p=pi/4;
xf=[-p 0 linspace(0,p,20)]; f=[0 0 sin(xf(3:end))];
plot([xf-2*p, xf, xf+2*p],[ f f f],'r','Linewidth',1.2)
axis equal; grid on; hold on
x=linspace(-3*p,3*p);
c0=(2-sqrt(2))/pi;
y=c0*ones(N+1,length(x));
for k=1:N
  ck=((-1)^k*(1+4*k*i)*sqrt(2)-2)/((16*k^2-1)*pi);
  tk=2*real(ck)*cos(4*k*x)-2*imag(ck)*sin(4*k*x);
  y(k+1,:)=y(k,:)+tk;
end
plot(x,y(2:inc:N,:));
% Para dibujar remarcada la última suma parcial
 plot(x,y(N+1,:),'k','Linewidth',1.2);
hold off
end