Enunciado
Encuentra el desarrollo en serie de Fourier de la función $f(x)$ 2-periódica, cuya representación en un período es
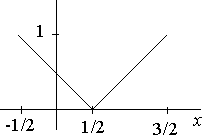
Resolución del primer apartado
Puesto que se cumplen las
condiciones para ser desarrollable en
serie de Fourier (condiciones de Dirichlet) y $p=1$,
el desarrollo de $f(x)$ y sus coeficientes son
$$f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty {\ a_n\cos n\pi x+b_n\sin n\pi x}$$$$a_n=\int_{-1}^{1}\ f(x)\cos n\pi x\, dx \ \ ,\ \ n=0, 1,\ldots\ \ ,\ \ b_n=\int_{-1}^{1}\ f(x)\sin n\pi x\, dx \ \ ,\ \ n=1, 2,\ldots$$
Ninguna de las opciones presentadas es correcta.
En vista de la la forma de la porción de $f(x)$ dibujada, se busca una trasladada que sea par en un periodo.
Las fórmulas son todas correctas, pero no es el procedimiento más adecuado para este caso.
No, míralo bien.
¡Sí! Esto ahorrará trabajo.
Una traslación que proporciona una función $g(x)$ par en $[-1,1]$ a partir de la función $f(x)$ es ... Piénsalo y pulsa en 'Ver' cuando lo tengas.
Ver
Podemos tomar
$$g(x)=f\left(x+\frac{1}{2}\right)\ \ \ \ \Rightarrow\ \ \ \ g(x)=\left\{\begin{array}{ccc}-x &\mbox{si} & -1<x<0 \\ x &\mbox{si} & 0<x<1\end{array}\right.$$
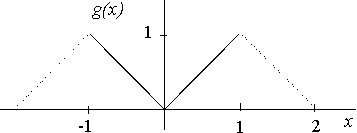
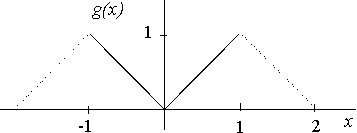
La ventaja de este método es que ahora sabemos que para esta función $g(x)$, simétrica par, todos los coeficientes $b_n$ son nulos y los $a_n$ son más sencillos de calcular (ver teoría)
$$g(x)=\frac{a_0}{2}+\sum_{n=1}^\infty {\ a_n\cos n\pi x} \ \ ,\ \ a_n=2\int_0^{1}\ x\cos n\pi x\, dx \ \ ,\ \ n=0, 1,\ldots$$
En particular, para $n=0$,
$$a_0=2\int_0^{1}\ x\, dx=1$$
Para los demás $n$, encontramos la primitiva correspondiente integrando por partes y hayamos el valor de la integral definida evaluando en los extremos, hazlo y pulsa después en 'Ver'
Ver
$$\int x\cos n\pi x\, dx=\frac{x}{n\pi}\mbox{sen} n\pi x-\frac{1}{n\pi}\int \sin n\pi x\, dx=\frac{x}{n\pi}\mbox{sen} n\pi x+\frac{1}{n^2\pi^2}\cos n\pi x+C$$
con lo cual
$$a_n=2\int_0^1 x\cos n\pi x\, dx=\frac{2}{n^2\pi^2}[(-1)^n-1]=\left\{\begin{array}{ccc} \frac{-4}{n^2\pi^2}&\text{si} & n \ \text{ impar}\\ 0 & \text{si}& n \ \text{par}\end{array}\right.$$
o bien
$$a_{2n-1}=\frac{-4}{(2n-1)^2\pi^2},\ n\geq 1\ \ \ \ ;\ \ \ \ a_{2n}=0,\ n\geq 1$$
El desarrollo de $g(x)$ es por tanto,
$g(x)=\frac{1}{2}-\frac{4}{\pi^2}\sum_{n=1}^\infty\ \frac{1}{(2n-1)^2}\cos {n\pi x}$
$g(x)=\frac{1}{2}-\frac{4}{\pi^2}\sum_{n=1}^\infty\ \frac{1}{(2n-1)^2}\cos {(2n-1)\pi x}$
¡No! Cuidado con el argumento de los cosenos.
¡Claro! Sólo hay armónicos de índice $n$ impar, luego si el sumatorio se toma sobre todos los naturales, debemos tomar $(2n-1)$ en los cosenos.
Retomamos ahora la función $f(x)$, puesto que $f(x)=g(x-\frac{1}{2})$, se tiene que
$$f(x)=g(x-\frac{1}{2})=\frac{1}{2}-\frac{4}{\pi^2}\sum_{n=1}^\infty\ \frac{1}{(2n-1)^2}\cos \left [(2n-1)\pi (x-\frac{1}{2})\right ]$$
pero entonces...
¡Esta expresión no es una serie de Fourier! esto de la traslación no ha valido para nada.
Este es el resultado y hemos terminado.
Debemos descomponer los cosenos.
En efecto, esa serie no está escrita en la forma habitual, pero todo lo anterior es válido y sólo falta trabajar un poco sobre los cosenos.
Es un buen resultado intermedio pero no puede dejarse como resultado final, deben escribirse de otro modo los cosenos.
En efecto, para encontrar la serie de Fourier en forma trigonométrica debemos descomponer los cosenos,
$$\cos\left [ (2n-1)\pi(x-\frac{1}{2})\right ]=\cos\left [ (2n-1)\pi x-(2n-1)\frac{\pi}{2}\right ]=$$$$=\cos\left [ (2n-1)\pi x \right ]\underbrace{\cos \left [(2n-1)\frac{\pi}{2}\right ]}_{=0}+\mbox{sen}\left [ (2n-1)\pi x \right ]\underbrace{\mbox{sen} \left [(2n-1)\frac{\pi}{2}\right ]}_{=(-1)^{n+1}}=(-1)^{n+1}\mbox{sen}\left [(2n-1)\pi x\right ]$$
y de esta manera obtenemos la serie de Fourier de $f(x)$,
$$f(x)=\frac{1}{2}+\frac{4}{\pi^2}\sum_{n=1}^\infty\ \frac{(-1)^{n}}{(2n-1)^2}\mbox{sen}\left [(2n-1)\pi x \right ]$$
Observaciones
Nótese que las amplitudes correspondientes a cada armónico de $f(x)$ y de su trasladada, $g(x)$, tienen el mismo valor absoluto. De hecho, la traslación en la variable $x$ únicamente supone un cambio de fase en los armónicos de la serie.
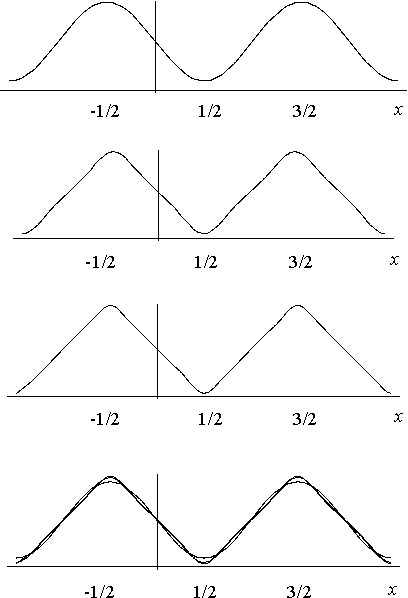
Aunque el objetivo de representar una función en serie de Fourier no es la aproximación, sí puede ser ilustrativo dibujar las curvas correspondientes a algunas sumas parciales y compararlas con la gráfica inicial.
Resumen
- Comprobar condiciones de desarrollabilidad y obtener $p$.
- Observar la forma de la función $f(x)$ para detectar simetrías y así deducir que una traslación conveniente convertirá en par esta función.
- Obtener el desarrollo de la trasladada par.
- Deshacer la traslación y escribir los armónicos en la forma habitual para obtener el desarrollo en forma trigonométrica.