Enunciado
- Encuentra el desarrollo en serie de Fourier de la función
definida por $f(x)=e^{-x}$ en el intervalo $[0,p]$ y periódica con periodo
$\pi$ en todo el eje real.
- Aplica el apartado anterior para calcular la suma de la serie numérica
$$\sum_{n=1}^\infty \frac{1}{4n^2+1}$$
Resolución del primer apartado
Hagamos en primer lugar un bosquejo de la función
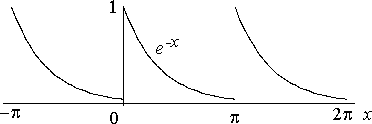
Esta función cumple las condiciones para ser desarrollable en serie de Fourier (condiciones de Dirichlet). Aquí el período es $\pi$, luego el semiperiodo es $p=\frac{\pi}{2}$. Entonces el desarrollo de $f$ ¿tiene la forma siguiente? $$S(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos 2nx+b_n\mbox{sen}\, 2nx$$
No, no es de esa forma.
Sí, así es el desarrollo.
Pues ese es el desarrollo, pero faltan los coeficientes.
En efecto, ése es el desarrollo, pero falta escribir cómo se calculan los coeficientes.
Los coeficientes $a_n$ y $b_n$ se calculan con las siguientes fórmulas:
$$a_n=\frac{2}{\pi}\int_{-\pi/2}^{\pi/2}\ e^{-x}\cos 2nx\, dx\ \, \ \ n=0,1,\ldots $$ $$b_n=\frac{2}{\pi}\int_{-\pi/2}^{\pi/2}\ e^{-x}\mbox{sen}\, 2nx\, dx \ \, \ \ n=1,2,\ldots$$
Las dos opciones son válidas.
$$a_n=\frac{2}{\pi}\int_{0}^{\pi}\ e^{-x}\cos 2nx\, dx\ \, \ \ n=0,1,\ldots $$ $$b_n=\frac{2}{\pi}\int_{0}^{\pi}\ e^{-x}\mbox{sen}\, 2nx\, dx \ \, \ \ n=1,2,\ldots$$
No, esos serían los coeficientes adecuados para la función que valiera $e^{-x}$ entre $-\frac{\pi}{2}$ y $\frac{\pi}{2}$:
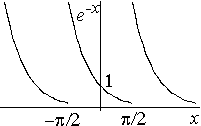
Míralo bien, ten en cuenta que la función de la que hay que hacer el desarrollo no es
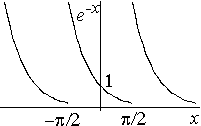
En efecto, recuerda que hay que tener cuidado en cómo se toma la función $f(x)$. Si el
dato del ejercicio es la expresión de la función en $[0,\pi]$ y en el resto de la
recta real se extiende periódicamente, ¡en $[-\frac{\pi}{2},0]$ la función no tiene la misma
expresión que en $[0,\frac{\pi}{2}]$. Para efectuar correctamente el cálculo de los coeficientes tenemos dos opciones
- buscar la expresión que toma nuestra función en $\left[-\frac{\pi}{2},\frac{\pi}{2}\right]$
- utilizar que si una función $g(x)$ es $T$-periódica, entonces $$\int_a^{a+T}\, g(x)\, dx=\int_0^T \, g(x)\, dx=\int_{-T/2}^{T/2} \, g(x)\, dx$$
Lo siguiente es el cálculo de esas integrales. Para $n=0$,
$$a_0=\frac{2}{\pi}\int_0^\pi\, e^{-x}\, dx=\frac{2}{\pi}(1-e^{-\pi})$$
Para los demás valores de $n$ hemos de conocer las primitivas
$$I=\int e^{-x}\cos 2nx\, dx \ \ \ \ ,\ \ \ \ J=\int e^{-x}\mbox{sen} 2nx\, dx$$
Podemos encontrar cada una de ellas integrando por partes dos veces o también siguiendo
el método que se expone a continuación. Considerar
$$I+iJ=\int e^{-x}(\cos 2nx+i\mbox{sen} 2nx)\, dx=\int e^{-x}e^{2nxi}\, dx=\int e^{(2ni-1)x}\, dx$$
Una vez resuelta esta última integral (proceso mucho más corto que el cálculo de
las primitivas anteriores), sabremos que su parte real es $I$ y $J$
su parte imaginaria:
$$\int e^{(2ni-1)x}\, dx=\frac{1}{2ni-1}e^{(2ni-1)x}=I+iJ$$
Encuentra la parte real y la parte imaginaria de esta expresión y pulsa en 'Ver'
Ver
$$I+iJ=-e^{-x}\frac{1+2ni}{4n^2+1}e^{2nix}=-e^{-x}\frac{1+2ni}{4n^2+1}(\cos 2nx+i\mbox{sen} 2nx)=\frac{-e^{-x}}{4n^2+1}[(cos 2nx-2n\mbox{sen} 2nx)+i(2n\cos 2nx+\mbox{sen} 2nx)] \ \ \ \Rightarrow $$
$$\Rightarrow \ \ \ I=\frac{e^{-x}}{4n^2+1}(2n\mbox{sen} 2nx-\cos 2nx)\ ,\ J=\frac{-e^{-x}}{4n^2+1}(2n\cos 2nx+\mbox{sen} 2nx)$$
Ahora sólo falta evaluar esas primitivas en los extremos de integración,
$$a_n=\frac{2}{\pi}\, I_0^{\pi}=\frac{2(1-e^{-\pi})}{\pi(4n^2+1)} \ \ ,\ \ b_n=\frac{2}{\pi}\, J_0^{\pi}=\frac{4n(1-e^{-\pi})}{\pi(4n^2+1)}$$
y sustituir en la fórmula inicial de la serie de Fourier
$$S(x)=\frac{1-e^{-\pi}}{\pi}\left[1+2\sum_{n=1}^\infty \frac{1}{4n^2+1}(\cos 2nx+2n\sin 2nx)\right]$$
Aunque el principal objetivo de escribir una función en serie de Fourier no es la aproximación, sí puede ser ilustrativo dibujar las curvas correspondientes
a algunas sumas parciales y compararlas con la gráfica inicial:
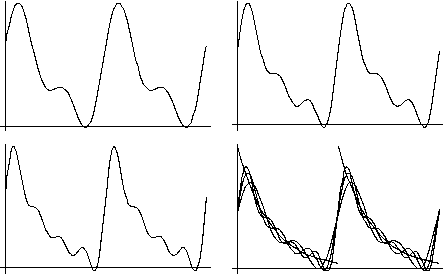
En la figura se muestran, de izquierda a derecha y de arriba a abajo, las sumas parciales de dos, tres y cuatro términos respectivamente, así como la superposición de los tres y de la curva inicial en un sólo gráfico.
Resolución del segundo apartado
Hemos de encontrar un valor de $x$ en el que evaluando la serie trigonométrica se pueda obtener la numérica. Es fácil observar que $$\sum_{n=1}^\infty \frac{1}{4n^2+1}(\cos 2n0+2n\sin 2n0)=\sum_{n=1}^\infty \frac{1}{4n^2+1}$$ Evaluamos por tanto $S(x)$ en $x=0$, $$S(0)=\frac{1-e^{-\pi}}{\pi}\left [1+2\sum_{n=1}^\infty \frac{1}{4n^2+1}\right ]$$ de aquí, $$\sum_{n=1}^\infty \frac{1}{4n^2+1}=\frac{1}{2}\left [\frac{\pi}{1-e^{-\pi}}S(0)-1\right ]$$ pero puesto que $S(x)$ es la representación en serie de Fourier de $f(x)$, conocemos que
$$S(0)=f(0)=e^0=1\ \ \ \Rightarrow \ \ \ \sum_{n=1}^\infty \frac{1}{4n^2+1}=\frac{\pi-1-e^{-\pi}}{2(1-e^{-\pi})}$$
$$S(0)=\frac{f^{+}(0)+f^{-}(0)}{2}$$
¡No! Eso sería así si la función fuera continua en $x=0$, pero esta $f(x)$ no lo es.
En efecto, la teoría nos asegura que la serie coincide con la función en los
puntos de continuidad y en los de discontinuidad la serie converge al promedio del
salto.

Tened en cuenta además que la función $f(x)$ (figura de la izquierda) no es $e^{-x}$ (figura de la derecha). $f(x)$ no es continua en $x=0$.
Con esto, la suma pedida es
$$\sum_{n=1}^\infty \frac{1}{4n^2+1}=\frac{1}{2}\left [\frac{\pi}{1-e^{-\pi}}S(0)-1\right ]=\frac{1}{2}\left [\frac{\pi (1+e^{-\pi})}{2(1-e^{-\pi})}-1\right ]=\frac{1}{2}\left [\frac{\pi}{2}\coth \frac{\pi}{2}-1\right ]$$
El valor aproximado de este número es 0.35634. El la tabla siguiente se recogen los valores aproximados de varias sumas parciales
de esta serie numérica. Se observa que es preciso sumar muchos términos para conseguir una buena aproximación.
| $N$ | $$\sim\sum_{n=1}^N\frac{1}{4n^2+1}$$ | $$\sim\sum_{n=1}^\infty\frac{1}{4n^2+1}$$ | |
| 10 | 0.32257 | ||
| 50 | 0.35139 | ||
| 100 | 0.35386 |
|
|
| 200 | 0.35535 | ||
| 500 | 0.35584 |