Dado un intervalo $[a,b]\in{\bf R}$, se llama partición de $[a,b]$ a un conjunto de puntos entre $a$ y $b$ $$P=\{x_0=a,\, x_1, \, \ldots , x_{n-1},\, x_n=b\}$$ que divide $[a,b]$ en $n$ subintervalos $$[a,b]=[x_0,x_1]\cup [x_1,x_2]\cup\ldots\cup[x_{n-1},x_n]$$ Se utiliza la siguiente notación $$\Delta x_i=x_i-x_{i-1}\ \ ,\ \ i=1,\, \ldots,\, n$$ y se llama norma de la partición al número $$||P||=\max_{1\leq i\leq n}\Delta x_i$$ es decir, a la longitud del intervalo más largo.

 

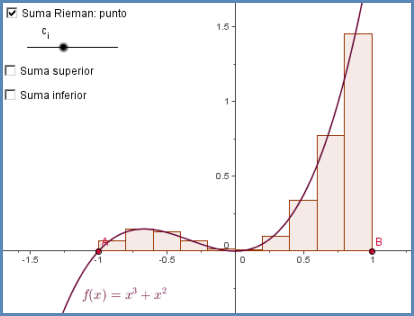
Consideramos ahora una función $f(x)$ definida en el intervalo $[a,b]$. Supondremos que $f(x)$ está acotada en $[a,b]$. Una suma de Riemann de $f(x)$ para la partición $P$ es un valor obtenido de la forma $$\sum_{i=1}^n f(c_i)\Delta x_i$$ siendo $c_i$ un punto entre $x_{i-1}$ y $x_i$, para cada $i$ entre 1 y $n$.

 

Laboratorio Sumas de Riemann

 

 

 

Cuestión: ¿Cuántas sumas de Riemann existen de una misma función sobre una misma partición?

 

Una vez construida la suma de Riemann, diremos que $f(x)$ es integrable según Riemann en $[a,b]$ si existe el siguiente límite $$\lim_{n\rightarrow \infty}\sum_{i=1}^n f(c_i)\Delta x_i\ \ ,\ \ c_i\in[x_{i-1},x_i]$$ Si este límite existe se le llama integral definida (según Riemann) de $f(x)$ en $[a,b]$ y se denota por $$\int_a^bf(x)\, dx$$

 

Importante: Si $f(x)$ es positiva, cada uno de los sumandos $f(c_i)\Delta x_i$ es el área del rectángulo de base $\Delta x_i$ y altura $f(c_i)$, de forma que la suma de Riemann proporciona una aproximación del área que queda bajo la curva $y=f(x)$ entre las rectas $x=a$ y $x=b$.