Enunciado
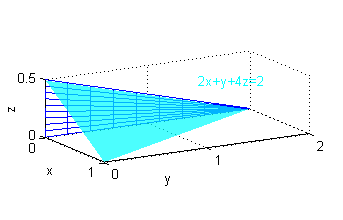
Sea \(S\) la superficie frontera del sólido \(H\)
situado en el primer octante y que está limitado por el plano \(2x+y+4z=2\). Calcula el flujo del campo vectorial $${\bf F}=x{\bf i}-{\bf j}+3z^2{\bf k}$$
hacia fuera de \(S\):
- Utilizando el teorema de Gauss
- Mediante integrales de superficie. (Ver ejercicio siguiente)
Paso 1
En primer lugar comprueba que se verifican las hipótesis del teorema de Gauss y pulsa en 'Ver' cuando termines.
Ver
En efecto se cumplen las condiciones para aplicar el teorema de la divergencia de Gauss, pues
- la superficie \(S\) es cerrada, suave por partes, por ser la unión de superficies suaves (porciones de planos) y se orientará con la normal hacia fuera
- el campo \(\bf{F}\) es de clase \(C^1\) en la superficie y su interior
Paso 2
Puesto que $$\mbox{div} {\bf F}=1+6z$$ la integral que hemos de calcular es $$\int\!\!\int\!\! \int_H (1+6z)\, dV$$ Vamos a integrar en el orden \(dx\, dy\, dz\), es decir con \(H\) descrito de la siguiente manera $$H=\{(x,y,z) / \, z_1\leq z\leq z_2,\ y_1(z)\leq y\leq y_2(z),\ x_1(y,z)\leq x\leq x_2(y,z)\}$$ Encuentra los límites de integración y pulsa en 'Ver'.
Ver
Tenemos
$$H=\{(x,y,z) / \, 0\leq z\leq \frac{1}{2},\ 0\leq y\leq 2-4z,\ 0\leq x\leq \frac{1}{2}(2-y-4z)\}$$
Paso 3
El último paso es el cálculo de la integral: $$I=\int_0^{\frac{1}{2}} \int_0^{2-4z} \int_0^\frac{2-y-4z}{2} (1+6z)\, dx\, dy\, dz$$ Realiza la primera integral y pulsa en 'Ver'
'Ver'
Tras calcular la integral en la variable \(x\), resulta
$$I=\int_0^{\frac{1}{2}} \int_0^{2-4z} (1+6z) ( 1-2z-\frac{1}{2}y ) \, dy\, dz$$
Realiza ahora la integral en la variable \(y\) y pulsa en 'Continuar'
Ahora tenemos
$$I=\int_0^{\frac{1}{2}} ( 1+2z-20z^2+24z^3) \, dz$$
que resulta ... Pulsa en 'Ver' cuando termines.
Ver
$$I=\left.z+z^2-\frac{20}{3}z^3+6z^4\right]_0^{\frac{1}{2}}=\frac{7}{24}$$
Resumen del primer apartado
- Aplicar el teorema de Gauss para convertir la integral de flujo en una integral triple
- Escribir los límites de integración de las iteradas de la integral triple
- Hallar las tres integrales.